1 . 已知四棱锥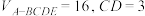 ,
,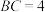 ,
, 平分
平分 ,点
,点 在
在 上且满足
上且满足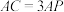 ,则三棱锥
,则三棱锥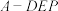 的体积为( )
的体积为( )
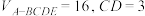 ,
,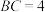 ,
, 平分
平分 ,点
,点 在
在 上且满足
上且满足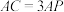 ,则三棱锥
,则三棱锥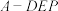 的体积为( )
的体积为( )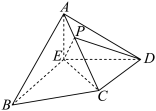
A.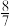 | B. | C.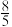 | D. |
您最近一年使用:0次
今日更新
|
173次组卷
|
3卷引用:江苏省锡山高级中学2023-2024学年高一下学期期末考试数学试题
江苏省锡山高级中学2023-2024学年高一下学期期末考试数学试题四川省广安市第二中学2024-2025学年高二上学期第一次月考数学试题(已下线)第一节 基本立体图形及表面积与体积【同步课时】 高三大一轮提升卷
名校
解题方法
2 . 一个正三棱锥高为 ,底面是边长为
,底面是边长为 的正三角形,则此三棱锥的侧面积为
的正三角形,则此三棱锥的侧面积为______ .
 ,底面是边长为
,底面是边长为 的正三角形,则此三棱锥的侧面积为
的正三角形,则此三棱锥的侧面积为
您最近一年使用:0次
名校
解题方法
3 . 如图,已知梯形 中,
中, ,四边形
,四边形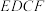 为矩形,
为矩形, ,平面
,平面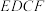 ⊥平面
⊥平面 ,点
,点 是
是 的中点.
的中点.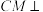 平面
平面 ;
;
(2)求异面直线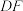 和
和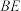 所成角的正弦值.
所成角的正弦值.
(3)求二面角 的余弦值;
的余弦值;
(4)若点 在线段
在线段 上,且直线
上,且直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段 的长.
的长.
 中,
中, ,四边形
,四边形 为矩形,
为矩形, ,平面
,平面 ⊥平面
⊥平面 ,点
,点 是
是 的中点.
的中点.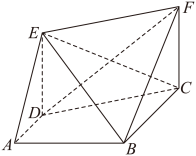
 平面
平面 ;
;(2)求异面直线
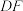 和
和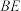 所成角的正弦值.
所成角的正弦值.(3)求二面角
 的余弦值;
的余弦值;(4)若点
 在线段
在线段 上,且直线
上,且直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段 的长.
的长.
您最近一年使用:0次
名校
解题方法
4 . 如图所示的几何体中,四边形ABCD为矩形,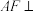 平面
平面 ,
,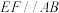 ,
,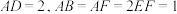 ,点P为棱DF的中点.
,点P为棱DF的中点.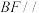 平面APC;
平面APC;
(2)求直线DE与平面BCF所成角的正弦值;
(3)求平面ACP与平面BCF的夹角的余弦值:
(4)求点F到平面ACP的距离.
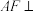 平面
平面 ,
,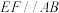 ,
,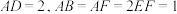 ,点P为棱DF的中点.
,点P为棱DF的中点.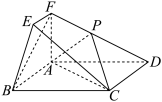
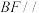 平面APC;
平面APC;(2)求直线DE与平面BCF所成角的正弦值;
(3)求平面ACP与平面BCF的夹角的余弦值:
(4)求点F到平面ACP的距离.
您最近一年使用:0次
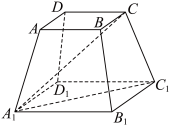
5 . 在正四棱台 中,
中, .
.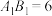 ,四棱台
,四棱台 的体积为
的体积为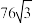 ,求该四棱台的高;
,求该四棱台的高;
(2)若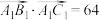 ,求
,求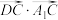 的值.
的值.
 中,
中, .
.
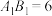 ,四棱台
,四棱台 的体积为
的体积为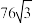 ,求该四棱台的高;
,求该四棱台的高;(2)若
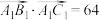 ,求
,求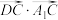 的值.
的值.
您最近一年使用:0次
解题方法
6 . 在长方体 中,
中, ,
,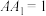 ,
, 是
是 的中点,点
的中点,点 在线段
在线段 上,若直线
上,若直线 与平面
与平面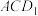 所成的角为
所成的角为 ,则
,则 的取值范围是( )
的取值范围是( )
 中,
中, ,
,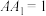 ,
, 是
是 的中点,点
的中点,点 在线段
在线段 上,若直线
上,若直线 与平面
与平面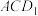 所成的角为
所成的角为 ,则
,则 的取值范围是( )
的取值范围是( )A. | B.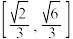 |
C.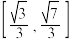 | D.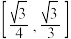 |
您最近一年使用:0次
名校
解题方法
7 . 在空间直角坐标系 中,已知向量
中,已知向量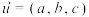 ,点
,点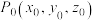 .若直线
.若直线 以
以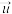 为方向向量且经过点
为方向向量且经过点 ,则直线
,则直线 的标准式方程可表示为
的标准式方程可表示为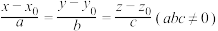 ;若平面
;若平面 以
以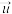 为法向量且经过点
为法向量且经过点 ,则平面
,则平面 的点法式方程表示为
的点法式方程表示为 .
.
(1)已知直线 的标准式方程为
的标准式方程为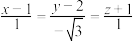 ,平面
,平面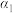 的点法式方程可表示为
的点法式方程可表示为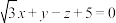 ,求直线
,求直线 与平面
与平面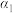 所成角的余弦值;
所成角的余弦值;
(2)已知平面 的点法式方程可表示为
的点法式方程可表示为 ,平面外一点
,平面外一点 ,求点
,求点 到平面
到平面 的距离;
的距离;
(3)(i)若集合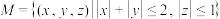 ,记集合
,记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 的体积:
的体积:
(ii)若集合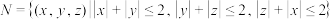 .记集合
.记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 相邻两个面(有公共棱)所成二面角的大小
相邻两个面(有公共棱)所成二面角的大小
 中,已知向量
中,已知向量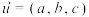 ,点
,点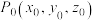 .若直线
.若直线 以
以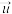 为方向向量且经过点
为方向向量且经过点 ,则直线
,则直线 的标准式方程可表示为
的标准式方程可表示为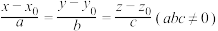 ;若平面
;若平面 以
以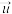 为法向量且经过点
为法向量且经过点 ,则平面
,则平面 的点法式方程表示为
的点法式方程表示为 .
.(1)已知直线
 的标准式方程为
的标准式方程为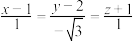 ,平面
,平面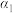 的点法式方程可表示为
的点法式方程可表示为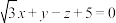 ,求直线
,求直线 与平面
与平面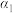 所成角的余弦值;
所成角的余弦值;(2)已知平面
 的点法式方程可表示为
的点法式方程可表示为 ,平面外一点
,平面外一点 ,求点
,求点 到平面
到平面 的距离;
的距离;(3)(i)若集合
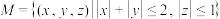 ,记集合
,记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 的体积:
的体积:(ii)若集合
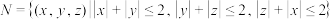 .记集合
.记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 相邻两个面(有公共棱)所成二面角的大小
相邻两个面(有公共棱)所成二面角的大小
您最近一年使用:0次
今日更新
|
106次组卷
|
2卷引用:湖南省长沙市明德中学2024-2025学年高二上学期10月阶段检测数学试卷
名校
解题方法
8 . 如图,在平行六面体 中,
中, ,
, ,
,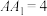 ,
, ,
, ,
, 是
是 的中点,设
的中点,设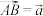 ,
,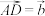 ,
,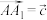 .
. 的长;
的长;
(2)求异面直线 和
和 夹角的余弦值.
夹角的余弦值.
 中,
中, ,
, ,
,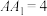 ,
, ,
, ,
, 是
是 的中点,设
的中点,设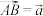 ,
,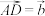 ,
,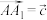 .
.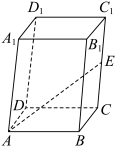
 的长;
的长;(2)求异面直线
 和
和 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
名校
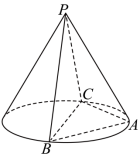
9 . 如图, 、
、 、
、 为圆锥三条母线,
为圆锥三条母线, .
.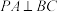 ;
;
(2)若圆锥侧面积为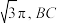 为底面直径,
为底面直径, ,求平面
,求平面 和平面
和平面 所成角的余弦值.
所成角的余弦值.
 、
、 、
、 为圆锥三条母线,
为圆锥三条母线, .
.
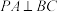 ;
;(2)若圆锥侧面积为
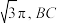 为底面直径,
为底面直径, ,求平面
,求平面 和平面
和平面 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
10 . 如图,在四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形,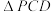 是边长为2的正三角形,
是边长为2的正三角形,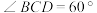 ,平面
,平面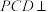 平面ABCD.
平面ABCD.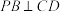 ;
;
(2)直线PB与平面APD所成角的正弦值;
(3)求平面APD与平面PCD夹角的余弦值.
 中,底面ABCD为菱形,
中,底面ABCD为菱形,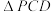 是边长为2的正三角形,
是边长为2的正三角形,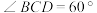 ,平面
,平面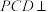 平面ABCD.
平面ABCD.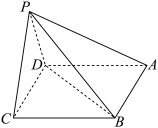
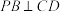 ;
;(2)直线PB与平面APD所成角的正弦值;
(3)求平面APD与平面PCD夹角的余弦值.
您最近一年使用:0次



