2024高三·全国·专题练习
解题方法
1 . 已知 ,
, 分别是椭圆
分别是椭圆 的左、右焦点,若椭圆C上存在点M使得
的左、右焦点,若椭圆C上存在点M使得 ,则椭圆C的离心率e的取值范围为( )
,则椭圆C的离心率e的取值范围为( )
 ,
, 分别是椭圆
分别是椭圆 的左、右焦点,若椭圆C上存在点M使得
的左、右焦点,若椭圆C上存在点M使得 ,则椭圆C的离心率e的取值范围为( )
,则椭圆C的离心率e的取值范围为( )A.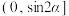 | B.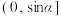 |
C. | D.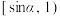 |
您最近半年使用:0次
2024·全国·模拟预测
2 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 在椭圆
在椭圆 上,且
上,且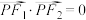 .若
.若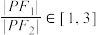 ,则椭圆
,则椭圆 的离心率的取值范围是( )
的离心率的取值范围是( )
 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 在椭圆
在椭圆 上,且
上,且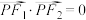 .若
.若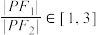 ,则椭圆
,则椭圆 的离心率的取值范围是( )
的离心率的取值范围是( )A.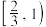 | B. | C.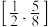 | D.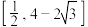 |
您最近半年使用:0次
解题方法
3 . 已知椭圆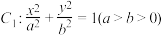 的左、右焦点分别为
的左、右焦点分别为 ,
,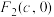 ,抛物线
,抛物线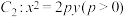 ,且椭圆
,且椭圆 与抛物线
与抛物线 相交于
相交于 两点,若
两点,若 ,则椭圆
,则椭圆 的离心率的取值范围是( )
的离心率的取值范围是( )
A.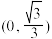 | B.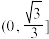 | C.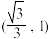 | D.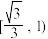 |
您最近半年使用:0次
解题方法
4 . 已知圆 的圆心为
的圆心为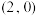 ,半径为4,圆
,半径为4,圆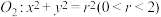 ,动圆M与圆
,动圆M与圆 ,圆
,圆 都相切,若动圆圆心M的轨迹是两个椭圆,且这两个椭圆的离心率分别为
都相切,若动圆圆心M的轨迹是两个椭圆,且这两个椭圆的离心率分别为 ,则
,则 的最小值为( )
的最小值为( )
 的圆心为
的圆心为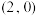 ,半径为4,圆
,半径为4,圆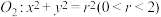 ,动圆M与圆
,动圆M与圆 ,圆
,圆 都相切,若动圆圆心M的轨迹是两个椭圆,且这两个椭圆的离心率分别为
都相切,若动圆圆心M的轨迹是两个椭圆,且这两个椭圆的离心率分别为 ,则
,则 的最小值为( )
的最小值为( )A.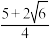 | B. | C. | D.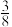 |
您最近半年使用:0次
解题方法
5 . 已知直线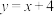 与椭圆
与椭圆 有公共点
有公共点 ,
, 的右焦点为
的右焦点为 ,则
,则 的离心率的最大值为
的离心率的最大值为______ .
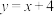 与椭圆
与椭圆 有公共点
有公共点 ,
, 的右焦点为
的右焦点为 ,则
,则 的离心率的最大值为
的离心率的最大值为
您最近半年使用:0次
名校
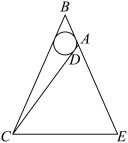
6 . 如图,在 中,已知
中,已知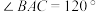 ,其内切圆与AC边相切于点D,且
,其内切圆与AC边相切于点D,且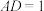 ,延长BA到E,使
,延长BA到E,使 ,连接CE,设以E,C为焦点且经过点A的椭圆的离心率为
,连接CE,设以E,C为焦点且经过点A的椭圆的离心率为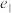 ,以E,C为焦点且经过点A的双曲线的离心率为
,以E,C为焦点且经过点A的双曲线的离心率为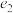 ,则
,则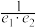 的取值范围是
的取值范围是______ .
 中,已知
中,已知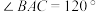 ,其内切圆与AC边相切于点D,且
,其内切圆与AC边相切于点D,且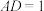 ,延长BA到E,使
,延长BA到E,使 ,连接CE,设以E,C为焦点且经过点A的椭圆的离心率为
,连接CE,设以E,C为焦点且经过点A的椭圆的离心率为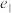 ,以E,C为焦点且经过点A的双曲线的离心率为
,以E,C为焦点且经过点A的双曲线的离心率为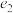 ,则
,则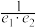 的取值范围是
的取值范围是
您最近半年使用:0次
名校
解题方法
7 . 已知农历每月的第 天
天 的月相外边缘近似为椭圆的一半,方程为
的月相外边缘近似为椭圆的一半,方程为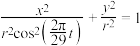 ,其中
,其中 为常数.根据以上信息,下列说法中正确的有( )
为常数.根据以上信息,下列说法中正确的有( )
①农历每月第 天和第
天和第 天的月相外边缘形状相同;
天的月相外边缘形状相同;
②月相外边缘上的点到椭圆焦点的距离的最大值为 ;
;
③月相外边缘的离心率第8天时取最大值;
④农历初六至初八的月相外边缘离心率在区间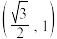 内.
内.
 天
天 的月相外边缘近似为椭圆的一半,方程为
的月相外边缘近似为椭圆的一半,方程为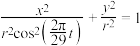 ,其中
,其中 为常数.根据以上信息,下列说法中正确的有( )
为常数.根据以上信息,下列说法中正确的有( )①农历每月第
 天和第
天和第 天的月相外边缘形状相同;
天的月相外边缘形状相同;②月相外边缘上的点到椭圆焦点的距离的最大值为
 ;
;③月相外边缘的离心率第8天时取最大值;
④农历初六至初八的月相外边缘离心率在区间
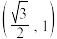 内.
内.| A.①③ | B.②④ | C.①② | D.③④ |
您最近半年使用:0次
2024-02-12更新
|
508次组卷
|
2卷引用:陕西省西安市长安区2024届高三第一次联考数学(理科)试题
名校
解题方法
8 . 如图,已知椭圆 的左、右焦点为
的左、右焦点为 、
、 ,
, 是椭圆上一点,
是椭圆上一点, 在
在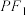 上,且满足
上,且满足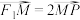 ,
,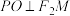 ,
, 为坐标原点,则椭圆离心率
为坐标原点,则椭圆离心率 的取值范围是
的取值范围是______ .
 的左、右焦点为
的左、右焦点为 、
、 ,
, 是椭圆上一点,
是椭圆上一点, 在
在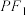 上,且满足
上,且满足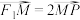 ,
,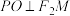 ,
, 为坐标原点,则椭圆离心率
为坐标原点,则椭圆离心率 的取值范围是
的取值范围是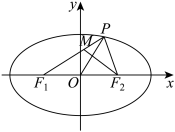
您最近半年使用:0次
解题方法
9 . 已知农历每月的第 天(
天( ,
,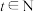 )的月相外边缘近似为椭圆的一半,方程为
)的月相外边缘近似为椭圆的一半,方程为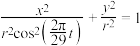 ,其中
,其中 为常数.根据以上信息,下列说法中正确的有( )
为常数.根据以上信息,下列说法中正确的有( )
 天(
天( ,
,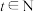 )的月相外边缘近似为椭圆的一半,方程为
)的月相外边缘近似为椭圆的一半,方程为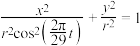 ,其中
,其中 为常数.根据以上信息,下列说法中正确的有( )
为常数.根据以上信息,下列说法中正确的有( )A.农历每月第 ( ( , ,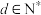 )天和第 )天和第 天的月相外边缘形状相同 天的月相外边缘形状相同 |
B.月相外边缘上的点到椭圆焦点的距离的最大值为 |
C.月相外边缘的离心率与 无关 无关 |
D.农历初六至初八的月相外边缘离心率在区间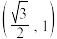 内 内 |
您最近半年使用:0次
名校
解题方法
10 . 设 、
、 是椭圆
是椭圆 :
: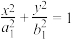 (
(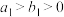 )与双曲线
)与双曲线 :
: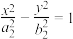 (
( ,
,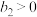 )的公共焦点,曲线
)的公共焦点,曲线 、
、 在第一象限内交于点
在第一象限内交于点 ,
,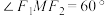 ,若椭圆的离心率
,若椭圆的离心率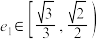 ,则双曲线的离心率
,则双曲线的离心率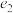 的取值范围是
的取值范围是______ .
 、
、 是椭圆
是椭圆 :
: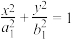 (
(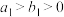 )与双曲线
)与双曲线 :
: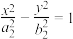 (
( ,
,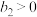 )的公共焦点,曲线
)的公共焦点,曲线 、
、 在第一象限内交于点
在第一象限内交于点 ,
,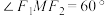 ,若椭圆的离心率
,若椭圆的离心率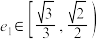 ,则双曲线的离心率
,则双曲线的离心率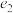 的取值范围是
的取值范围是
您最近半年使用:0次
2024-01-22更新
|
498次组卷
|
3卷引用:四川省内江市2023-2024学年高二上学期1月期末检测数学试题



