1 . 已知直线 :
: 与双曲线
与双曲线 :
: 交于
交于 ,
, 两点,点
两点,点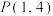 是弦
是弦 的中点,则双曲线
的中点,则双曲线 的渐近线方程是( )
的渐近线方程是( )
 :
: 与双曲线
与双曲线 :
: 交于
交于 ,
, 两点,点
两点,点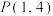 是弦
是弦 的中点,则双曲线
的中点,则双曲线 的渐近线方程是( )
的渐近线方程是( )A.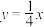 | B. | C. | D. |
您最近一年使用:0次
2024-08-19更新
|
1171次组卷
|
5卷引用:2025届广东省肇庆市碧海湾学校、肇庆博纳实验学校2024-2025学年高三上学期联合模拟数学试题
2025届广东省肇庆市碧海湾学校、肇庆博纳实验学校2024-2025学年高三上学期联合模拟数学试题宁夏2025届高三8月新起点调研模拟试卷(一)数学试题(已下线)9.4 点差法与定值、定点和最值(讲义)(已下线)第08讲 直线与圆锥曲线的位置关系(八大题型)(练习)-2江苏省徐州市铜山区大许中学2024-2025学年高二上学期第一次月考数学试卷.
名校
解题方法
2 . 已知点F,A分别是椭圆 的左焦点、右顶点,
的左焦点、右顶点, 满足
满足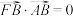 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )
 的左焦点、右顶点,
的左焦点、右顶点, 满足
满足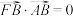 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )A.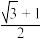 | B.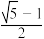 | C. | D.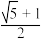 |
您最近一年使用:0次
解题方法
3 . 设 两点的坐标分别为
两点的坐标分别为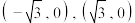 . 直线
. 直线 相交于点
相交于点 ,且它们的斜率之积是
,且它们的斜率之积是 . 设点
. 设点 的轨迹方程为
的轨迹方程为 .
.
(1)求 ;
;
(2)不经过点 的直线
的直线 与曲线
与曲线 相交于
相交于 、
、 两点,且直线
两点,且直线 与直线
与直线 的斜率之积是
的斜率之积是 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
 两点的坐标分别为
两点的坐标分别为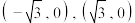 . 直线
. 直线 相交于点
相交于点 ,且它们的斜率之积是
,且它们的斜率之积是 . 设点
. 设点 的轨迹方程为
的轨迹方程为 .
.(1)求
 ;
;(2)不经过点
 的直线
的直线 与曲线
与曲线 相交于
相交于 、
、 两点,且直线
两点,且直线 与直线
与直线 的斜率之积是
的斜率之积是 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
您最近一年使用:0次
名校
4 . 已知定义在 上的函数
上的函数 的图象连续不间断,当
的图象连续不间断,当 ,且当
,且当 时,
时,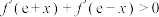 ,则下列说法正确的是()
,则下列说法正确的是()
 上的函数
上的函数 的图象连续不间断,当
的图象连续不间断,当 ,且当
,且当 时,
时,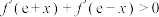 ,则下列说法正确的是()
,则下列说法正确的是()A. |
B. 在 在 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C.若 ,则 ,则 |
D.若 是 是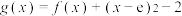 在 在 内的两个零点,且 内的两个零点,且 ,则 ,则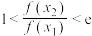 |
您最近一年使用:0次
2024-08-16更新
|
1479次组卷
|
3卷引用:2025届广东省高三毕业班调研考试(一)数学试卷
名校
解题方法
5 . 已知椭圆的方程为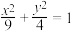 ,过椭圆中心的直线交椭圆于A、B两点,
,过椭圆中心的直线交椭圆于A、B两点, 是椭圆的右焦点,则
是椭圆的右焦点,则 的周长的最小值为( )
的周长的最小值为( )
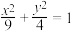 ,过椭圆中心的直线交椭圆于A、B两点,
,过椭圆中心的直线交椭圆于A、B两点, 是椭圆的右焦点,则
是椭圆的右焦点,则 的周长的最小值为( )
的周长的最小值为( )| A.8 | B.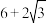 | C.10 | D.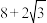 |
您最近一年使用:0次
2024-08-15更新
|
1813次组卷
|
5卷引用:广东省博罗县博罗中学2024届高三高考考前最后一卷数学试题
广东省博罗县博罗中学2024届高三高考考前最后一卷数学试题(已下线)9.1 椭圆(讲义)(已下线)第05讲 椭圆及其性质(九大题型)(讲义)-1江苏省连云港市高级中学2024-2025学年高二上学期第一次阶段检测(9月)数学试题(已下线)微点14、椭圆方程与性质(二)【练】 -同步微点进阶
解题方法
6 . 如图,在 中,AC边上的高为BH,且
中,AC边上的高为BH,且 ,矩形DEFG的顶点D,G分别在边BA,BC上,E,F都在边AC上,以AC为轴将
,矩形DEFG的顶点D,G分别在边BA,BC上,E,F都在边AC上,以AC为轴将 旋转一周,则矩形DEFG旋转形成的几何体的最大体积为( )
旋转一周,则矩形DEFG旋转形成的几何体的最大体积为( )
 中,AC边上的高为BH,且
中,AC边上的高为BH,且 ,矩形DEFG的顶点D,G分别在边BA,BC上,E,F都在边AC上,以AC为轴将
,矩形DEFG的顶点D,G分别在边BA,BC上,E,F都在边AC上,以AC为轴将 旋转一周,则矩形DEFG旋转形成的几何体的最大体积为( )
旋转一周,则矩形DEFG旋转形成的几何体的最大体积为( )
A.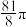 | B.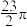 | C. | D.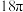 |
您最近一年使用:0次
解题方法
7 . 已知椭圆 的右焦点为
的右焦点为 ,
, 分别为椭圆
分别为椭圆 的左、右顶点,
的左、右顶点, 分别为椭圆
分别为椭圆 的上、下顶点,四边形
的上、下顶点,四边形 的面积为
的面积为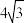 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 且斜率不为
且斜率不为 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,直线
两点,直线 与
与 的交点为
的交点为 .
.
①若直线 的倾斜角为
的倾斜角为 ,求线段
,求线段 的长度;
的长度;
②试问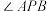 是否有最大值?如果有,求出
是否有最大值?如果有,求出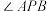 的最大值;如果没有,说明理由.
的最大值;如果没有,说明理由.
 的右焦点为
的右焦点为 ,
, 分别为椭圆
分别为椭圆 的左、右顶点,
的左、右顶点, 分别为椭圆
分别为椭圆 的上、下顶点,四边形
的上、下顶点,四边形 的面积为
的面积为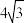 .
.(1)求椭圆
 的方程;
的方程;(2)过点
 且斜率不为
且斜率不为 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,直线
两点,直线 与
与 的交点为
的交点为 .
.①若直线
 的倾斜角为
的倾斜角为 ,求线段
,求线段 的长度;
的长度;②试问
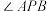 是否有最大值?如果有,求出
是否有最大值?如果有,求出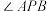 的最大值;如果没有,说明理由.
的最大值;如果没有,说明理由.
您最近一年使用:0次
8 . 已知双曲线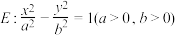 的离心率
的离心率 ,圆
,圆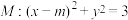 与双曲线E的渐近线相切,则
与双曲线E的渐近线相切,则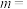
_________ .
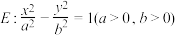 的离心率
的离心率 ,圆
,圆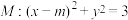 与双曲线E的渐近线相切,则
与双曲线E的渐近线相切,则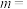
您最近一年使用:0次
9 . 已知M是抛物线 上的一点,F是抛物线的焦点,以
上的一点,F是抛物线的焦点,以 为始边、
为始边、 为终边的角
为终边的角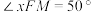 ,则点M的横坐标为( )
,则点M的横坐标为( )
 上的一点,F是抛物线的焦点,以
上的一点,F是抛物线的焦点,以 为始边、
为始边、 为终边的角
为终边的角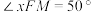 ,则点M的横坐标为( )
,则点M的横坐标为( )A.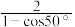 | B.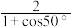 | C.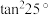 | D.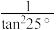 |
您最近一年使用:0次
名校
10 . 已知曲线C是平面内到定点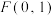 和定直线l:
和定直线l: 的距离之和等于4的点的轨迹,若
的距离之和等于4的点的轨迹,若 在曲线C上,则( )
在曲线C上,则( )
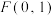 和定直线l:
和定直线l: 的距离之和等于4的点的轨迹,若
的距离之和等于4的点的轨迹,若 在曲线C上,则( )
在曲线C上,则( )| A.曲线C关于x轴对称 |
B.曲线C上任意一点到原点的距离都不超过 |
| C.曲线C及其内部共包含了19个整点(即横、纵坐标均为整数的点) |
D.点 到点 到点 和点 和点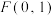 的距离之和最小为 的距离之和最小为 |
您最近一年使用:0次
2024-08-08更新
|
317次组卷
|
3卷引用:广东省广州市2023届高三冲刺(一)数学试题



