1 . 现有6名孩子和3个不同的房间,并让孩子都进入房间.
(1)若每个房间进2个小孩,共有多少种不同的方法?
(2)恰有一个房间没有孩子,共有多少种安排方法?
(1)若每个房间进2个小孩,共有多少种不同的方法?
(2)恰有一个房间没有孩子,共有多少种安排方法?
您最近一年使用:0次
名校
解题方法
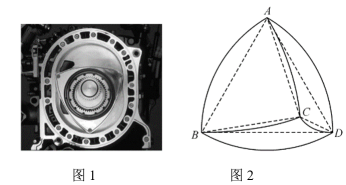
2 . 在世界环保意识日益强化,石油资源日渐沽竭的今天,以氢气做动力源的研究已成为一大课题.当年马自达坚持下来的转子发动机(如图1)从结构上讲是最适合燃烧氢气,而且最“干净”,因为氢燃烧完后排出的是水蒸气,对环境没有任何污染.马自达公司改制了RX-7型跑车的转子发动机,使它可以用氢做燃料.以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的相交部分围成的几何体(如图2)被称为“勒洛四面体”,它表面上任意两点间的距离最大值与正四面体棱长相等,能在两个平行平面间自由转动,并且始终保持与两平面都接触,因此它能像球一样来回滚动.转子发动机的设计正是利用了这一原理.转子引擎只需转一周,各转子便有一次进气、压缩、点火与排气过程,相当于往复式引擎运转两周,因此具有小排气量就能成就高动力输出的优点.另外,由于转子引擎的轴向运动特性,它不需要精密的曲轴平衡就可以达到非常高的运转转速.若正四面体ABCD的棱长为2,将对应的勒洛四面体ABCD放进一个正方体纸盒中,若该勒洛四面体可以在纸盒内任意转动,则该纸盒棱长的最小值为__________ ;若在勒洛四面体ABCD内放一个小正方体零件,该零件可以在勒洛四面体ABCD内任意转动,则该零件棱长的最大值为__________ .
您最近一年使用:0次
7日内更新
|
29次组卷
|
2卷引用:云南省曲靖市民族中学2022-2023学年高二上学期教学测评开学考试数学试卷
3 . 若函数 存在零点
存在零点 ,函数
,函数 存在零点
存在零点 ,使得
,使得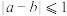 ,则称
,则称 与
与 互为亲密函数.
互为亲密函数.
(1)判断函数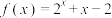 与
与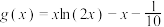 是否为亲密函数,并说明理由;
是否为亲密函数,并说明理由;
(2)若 与
与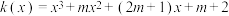 互为亲密函数,求
互为亲密函数,求 的取值范围.
的取值范围.
附: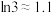 .
.
 存在零点
存在零点 ,函数
,函数 存在零点
存在零点 ,使得
,使得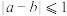 ,则称
,则称 与
与 互为亲密函数.
互为亲密函数.(1)判断函数
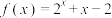 与
与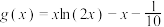 是否为亲密函数,并说明理由;
是否为亲密函数,并说明理由;(2)若
 与
与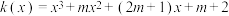 互为亲密函数,求
互为亲密函数,求 的取值范围.
的取值范围.附:
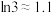 .
.
您最近一年使用:0次
7日内更新
|
199次组卷
|
4卷引用:云南省部分校2023-2024学年高二下学期月考联考数学试题
解题方法
4 . 已知椭圆 :
: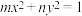 经过
经过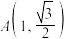 ,
,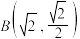 ,
,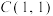 ,
,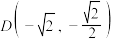 ,
,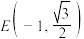 这5个点中的4个点.
这5个点中的4个点.
(1)求 的方程.
的方程.
(2)设直线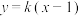 与
与 交于不同的两点
交于不同的两点 ,
,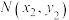 .
.
①证明:存在常数 ,使得
,使得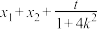 为定值.
为定值.
②若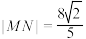 ,求
,求 的值.
的值.
 :
: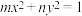 经过
经过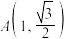 ,
,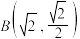 ,
,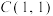 ,
,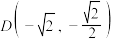 ,
,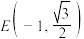 这5个点中的4个点.
这5个点中的4个点.(1)求
 的方程.
的方程.(2)设直线
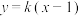 与
与 交于不同的两点
交于不同的两点 ,
,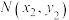 .
.①证明:存在常数
 ,使得
,使得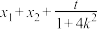 为定值.
为定值.②若
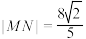 ,求
,求 的值.
的值.
您最近一年使用:0次
名校
解题方法
5 . 贝叶斯公式 中,
中, 称为先验概率,
称为先验概率,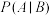 称为后验概率.先验概率
称为后验概率.先验概率 表达了对事件
表达了对事件 的初始判断,当新的信息
的初始判断,当新的信息 出现后,我们可以利用贝叶斯公式求出后验概率
出现后,我们可以利用贝叶斯公式求出后验概率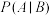 ,以此修正自己的判断并校正决策.利用这种思想方法我们来解决如下一个实际问题.
,以此修正自己的判断并校正决策.利用这种思想方法我们来解决如下一个实际问题.
某趣味抽奖活动准备了三个外观相同的不透明箱子,已知三个箱子中分别装有10个红球、5个红球5个白球、10个白球(球的大小、质地相同).抽奖活动共设计了两个轮次:
第一轮规则:抽奖者从三个箱子中随机选择一个箱子,并从该箱子中取出两球(分两次取出,每次取一球,取出的球不放回),若取出的两个球都是红球则可以进入第二轮,否则抽奖活动结束(无奖金).
第二轮规则:进入第二轮的抽奖者可以选择三种抽奖方案.方案一:就此停止,并获得奖金300元;方案二:继续从第一轮抽取的箱子中再取一球,若为红球则可获得奖金400元,若为白球奖金变为0元;方案三:不再从第一轮抽取的箱子中取球,而是从另外两个箱子中随机选择一个箱子,并从中取出一球,若为红球则可获得奖金800元,若为白球奖金变为80元.
(1)求抽奖者在第一次取出红球的条件下,能进入第二轮的概率;
(2)在第二轮的三种抽奖方案中,从抽奖者获得奖金的数学期望的角度,找出三种抽奖方案的最佳方案.
 中,
中, 称为先验概率,
称为先验概率,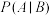 称为后验概率.先验概率
称为后验概率.先验概率 表达了对事件
表达了对事件 的初始判断,当新的信息
的初始判断,当新的信息 出现后,我们可以利用贝叶斯公式求出后验概率
出现后,我们可以利用贝叶斯公式求出后验概率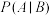 ,以此修正自己的判断并校正决策.利用这种思想方法我们来解决如下一个实际问题.
,以此修正自己的判断并校正决策.利用这种思想方法我们来解决如下一个实际问题.某趣味抽奖活动准备了三个外观相同的不透明箱子,已知三个箱子中分别装有10个红球、5个红球5个白球、10个白球(球的大小、质地相同).抽奖活动共设计了两个轮次:
第一轮规则:抽奖者从三个箱子中随机选择一个箱子,并从该箱子中取出两球(分两次取出,每次取一球,取出的球不放回),若取出的两个球都是红球则可以进入第二轮,否则抽奖活动结束(无奖金).
第二轮规则:进入第二轮的抽奖者可以选择三种抽奖方案.方案一:就此停止,并获得奖金300元;方案二:继续从第一轮抽取的箱子中再取一球,若为红球则可获得奖金400元,若为白球奖金变为0元;方案三:不再从第一轮抽取的箱子中取球,而是从另外两个箱子中随机选择一个箱子,并从中取出一球,若为红球则可获得奖金800元,若为白球奖金变为80元.
(1)求抽奖者在第一次取出红球的条件下,能进入第二轮的概率;
(2)在第二轮的三种抽奖方案中,从抽奖者获得奖金的数学期望的角度,找出三种抽奖方案的最佳方案.
您最近一年使用:0次
2024·全国·模拟预测
6 . 2023年11月19日,以“激发创新活力,提升发展质量”为主题的第二十五届中国国际高新技术成果交易会(以下简称“高交会”)在深圳闭幕,作为“中国科技第一展”的高交会距今已有25年的历史.福田展区的专业展设有新一代信息技术展、环保展、新型显示展、智慧城市展、数字医疗展、高端装备制造展等六类.现统计了每个展区的备受关注率﹝一个展区中受到所有相关人士(或企业)关注的企业数与该展区的参展企业数的比值﹞,如下表:
(1)从参展的6个展区的企业中随机选取一家企业,求这家企业是“新型显示展”展区备受关注的企业的概率.
(2)若视备受关注率为概率,某电视台现要从“环保展”“智慧城市展”“高端装备制造展”3个展区中随机抽取2个展区,再从抽出的2个展区中各抽取一家企业进行采访,求采访的两家企业都是备受关注的企业的概率.
(3)从“新一代信息技术展”展区备受关注的企业和“数字医疗展”展区备受关注的企业中,任选2家接受记者采访.记 为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量
为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量 的分布列和数学期望.
的分布列和数学期望.
| 展区类型 | 新一代信 息技术展 | 环保展 | 新型显示展 | 智慧城市展 | 数字医疗展 | 高端装备 制造展 |
| 展区的企 业数量/家 | 60 | 360 | 650 | 450 | 70 | 990 |
| 备受关注率 | 0.20 | 0.10 | 0.24 | 0.30 | 0.10 | 0.20 |
(2)若视备受关注率为概率,某电视台现要从“环保展”“智慧城市展”“高端装备制造展”3个展区中随机抽取2个展区,再从抽出的2个展区中各抽取一家企业进行采访,求采访的两家企业都是备受关注的企业的概率.
(3)从“新一代信息技术展”展区备受关注的企业和“数字医疗展”展区备受关注的企业中,任选2家接受记者采访.记
 为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量
为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
解题方法
7 . Unidentified Flying Object,简称UFO,俗称飞碟,通常被人们看作是外地文明派到地球的使者.为了调查国内网友对UFO的了解情况,资深UFO爱好者李磊,在网上发起了一项“UFO”有奖问答,共有10000名网友参加,李磊随机抽取了1000名(得分都在60~100分之间),将得分分成4组: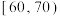 ,
,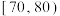 ,
,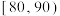 ,
,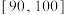 ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图: 的高分网友发放奖品,试估计这次有奖问答的获奖分数线;(保留一位小数)
的高分网友发放奖品,试估计这次有奖问答的获奖分数线;(保留一位小数)
(2)用分层随机抽样的方法从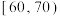 ,
,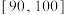 两个分数段共抽取出4名网友,再从这4名网友中随机抽取2名依次分享UFO时间供大家交流,求第一个分享的网友得分在
两个分数段共抽取出4名网友,再从这4名网友中随机抽取2名依次分享UFO时间供大家交流,求第一个分享的网友得分在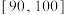 的概率.
的概率.
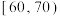 ,
,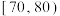 ,
,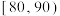 ,
,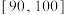 ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图: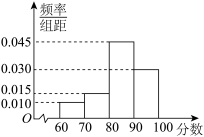
 的高分网友发放奖品,试估计这次有奖问答的获奖分数线;(保留一位小数)
的高分网友发放奖品,试估计这次有奖问答的获奖分数线;(保留一位小数)(2)用分层随机抽样的方法从
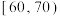 ,
,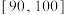 两个分数段共抽取出4名网友,再从这4名网友中随机抽取2名依次分享UFO时间供大家交流,求第一个分享的网友得分在
两个分数段共抽取出4名网友,再从这4名网友中随机抽取2名依次分享UFO时间供大家交流,求第一个分享的网友得分在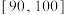 的概率.
的概率.
您最近一年使用:0次
8 . 某射击小组有甲、乙两名运动员,其中甲、乙二人射击成绩优秀的概率分别为 ,且两人射击成绩是否优秀相互独立.
,且两人射击成绩是否优秀相互独立.
(1)若甲、乙两人各射击一次,求至多1人射击成绩优秀的概率;
(2)在一次训练中,甲、乙各连续射击10次,甲击中环数的平均数为7.8,方差为1.6,乙击中环数的平均数为8.2,方差为2.8,求两人在这20次射击中击中环数的方差.
 ,且两人射击成绩是否优秀相互独立.
,且两人射击成绩是否优秀相互独立.(1)若甲、乙两人各射击一次,求至多1人射击成绩优秀的概率;
(2)在一次训练中,甲、乙各连续射击10次,甲击中环数的平均数为7.8,方差为1.6,乙击中环数的平均数为8.2,方差为2.8,求两人在这20次射击中击中环数的方差.
您最近一年使用:0次
名校
9 . 球面被平面所截得的一部分叫做球冠(如图).球冠是曲面,是球面的一部分.截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高.阿基米德曾在著作《论球与圆柱》中记录了一个被后人称作“Archimedes’Hat-BoxTheorem”的定理:球冠的表面积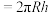 (如上图,这里的表面积不含底面的圆的面积).某同学制作了一个工艺品,如下图所示.该工艺品可以看成是一个球被一个棱长为4的正方体的六个面所截后剩余的部分(球心与正方体的中心重合),即一个球去掉了6个球冠后剩下的部分.若其中一个截面圆的周长为
(如上图,这里的表面积不含底面的圆的面积).某同学制作了一个工艺品,如下图所示.该工艺品可以看成是一个球被一个棱长为4的正方体的六个面所截后剩余的部分(球心与正方体的中心重合),即一个球去掉了6个球冠后剩下的部分.若其中一个截面圆的周长为 ,则该工艺品的表面积为( )
,则该工艺品的表面积为( )
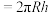 (如上图,这里的表面积不含底面的圆的面积).某同学制作了一个工艺品,如下图所示.该工艺品可以看成是一个球被一个棱长为4的正方体的六个面所截后剩余的部分(球心与正方体的中心重合),即一个球去掉了6个球冠后剩下的部分.若其中一个截面圆的周长为
(如上图,这里的表面积不含底面的圆的面积).某同学制作了一个工艺品,如下图所示.该工艺品可以看成是一个球被一个棱长为4的正方体的六个面所截后剩余的部分(球心与正方体的中心重合),即一个球去掉了6个球冠后剩下的部分.若其中一个截面圆的周长为 ,则该工艺品的表面积为( )
,则该工艺品的表面积为( )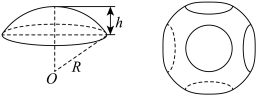
A.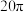 | B.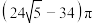 | C. | D. |
您最近一年使用:0次
2024-04-05更新
|
1084次组卷
|
4卷引用:云南省昆明市第八中学2023-2024学年高二下学期月考二数学试卷
名校
10 . 某工厂生产某种元件,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品,现抽取这种元件100件进行检测,检测结果统计如下表:
(1)现从这100件样品中随机抽取2件,若其中一件为合格品,求另一件也为合格品的概率;
(2)关于随机变量,俄国数学家切比雪夫提出切比雪夫不等式:
若随机变量X具有数学期望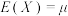 ,方差
,方差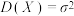 ,则对任意正数
,则对任意正数 ,均有
,均有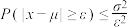 成立.
成立.
(i)若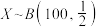 ,证明:
,证明: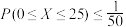 ;
;
(ii)利用该结论表示即使分布未知,随机变量的取值范围落在期望左右的一定范围内的概率是有界的.若该工厂声称本厂元件合格率为90%,那么根据所给样本数据,请结合“切比雪夫不等式”说明该工厂所提供的合格率是否可信?(注:当随机事件A发生的概率小于0.05时,可称事件A为小概率事件)
| 测试指标 | 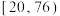 | 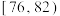 | 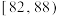 | 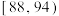 |  |
| 元件数(件) | 12 | 18 | 36 | 30 | 4 |
(2)关于随机变量,俄国数学家切比雪夫提出切比雪夫不等式:
若随机变量X具有数学期望
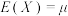 ,方差
,方差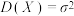 ,则对任意正数
,则对任意正数 ,均有
,均有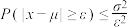 成立.
成立.(i)若
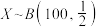 ,证明:
,证明: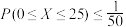 ;
;(ii)利用该结论表示即使分布未知,随机变量的取值范围落在期望左右的一定范围内的概率是有界的.若该工厂声称本厂元件合格率为90%,那么根据所给样本数据,请结合“切比雪夫不等式”说明该工厂所提供的合格率是否可信?(注:当随机事件A发生的概率小于0.05时,可称事件A为小概率事件)
您最近一年使用:0次
2024-03-21更新
|
2661次组卷
|
6卷引用:云南省昆明市第三中学2023-2024学年高二下学期5月期中考试数学试题
云南省昆明市第三中学2023-2024学年高二下学期5月期中考试数学试题(已下线)第七章 随机变量及其分布(提升卷)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)浙江省金丽衢十二校2024届高三下学期第二次联考数学试题辽宁省2024届高三下学期3+2+1模式新高考适应性统一考试数学试卷江苏省姜堰中学2024届高三下学期阶段性测试(2.5模)数学试题(已下线)浙江省金丽衢十二校2024届高三下学期第二次联考数学试题变式题16-19



