1 . 已知函数 与
与 的图象关于直线
的图象关于直线 对称,若
对称,若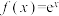 ,构造函数
,构造函数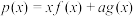 .
.
(1)当 时,求函数
时,求函数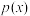 在点
在点 处的切线与坐标轴围成三角形的面积;
处的切线与坐标轴围成三角形的面积;
(2)若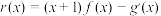 (其中
(其中 为
为 的导函数),当
的导函数),当 时,
时, ,证明:
,证明: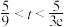 .(参考数据:
.(参考数据: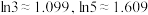 )
)
 与
与 的图象关于直线
的图象关于直线 对称,若
对称,若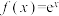 ,构造函数
,构造函数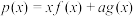 .
.(1)当
 时,求函数
时,求函数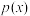 在点
在点 处的切线与坐标轴围成三角形的面积;
处的切线与坐标轴围成三角形的面积;(2)若
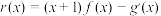 (其中
(其中 为
为 的导函数),当
的导函数),当 时,
时, ,证明:
,证明: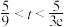 .(参考数据:
.(参考数据: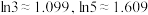 )
)
您最近一年使用:0次
名校
2 . 已知函数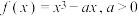 .
.
(1)当 时,求出函数在点
时,求出函数在点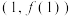 处的切线方程.
处的切线方程.
(2)如图所示,函数 图像上一点
图像上一点 处的切线与函数图像交于点
处的切线与函数图像交于点 ,过
,过 的切线
的切线 (
( 为切点)与
为切点)与 处的切线交于点
处的切线交于点 .问:三角形
.问:三角形 是否可能是等边三角形?若是,求此时
是否可能是等边三角形?若是,求此时 的值;若不是,说明理由.
的值;若不是,说明理由.
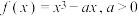 .
.(1)当
 时,求出函数在点
时,求出函数在点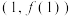 处的切线方程.
处的切线方程.(2)如图所示,函数
 图像上一点
图像上一点 处的切线与函数图像交于点
处的切线与函数图像交于点 ,过
,过 的切线
的切线 (
( 为切点)与
为切点)与 处的切线交于点
处的切线交于点 .问:三角形
.问:三角形 是否可能是等边三角形?若是,求此时
是否可能是等边三角形?若是,求此时 的值;若不是,说明理由.
的值;若不是,说明理由.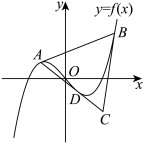
您最近一年使用:0次
3 . 已知抛物线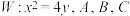 是
是 上不同的三点,过三点的三条切线分别两两交于点
上不同的三点,过三点的三条切线分别两两交于点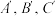 ,则称三角形
,则称三角形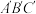 为抛物线的外切三角形.
为抛物线的外切三角形.
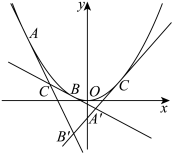
(1)当点 的坐标为
的坐标为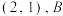 为坐标原点,且
为坐标原点,且 时,求点
时,求点 的坐标;
的坐标;
(2)设外切三角形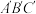 的垂心为
的垂心为 ,试判断
,试判断 是否在定直线上,若是,求出该定直线;若不是,请说明理由;
是否在定直线上,若是,求出该定直线;若不是,请说明理由;
(3)证明:三角形 与外切三角形
与外切三角形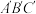 的面积之比为定值.
的面积之比为定值.
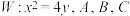 是
是 上不同的三点,过三点的三条切线分别两两交于点
上不同的三点,过三点的三条切线分别两两交于点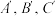 ,则称三角形
,则称三角形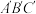 为抛物线的外切三角形.
为抛物线的外切三角形.
(1)当点
 的坐标为
的坐标为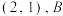 为坐标原点,且
为坐标原点,且 时,求点
时,求点 的坐标;
的坐标;(2)设外切三角形
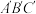 的垂心为
的垂心为 ,试判断
,试判断 是否在定直线上,若是,求出该定直线;若不是,请说明理由;
是否在定直线上,若是,求出该定直线;若不是,请说明理由;(3)证明:三角形
 与外切三角形
与外切三角形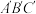 的面积之比为定值.
的面积之比为定值.
您最近一年使用:0次
名校
解题方法
4 . 已知函数 .
.
(1)当 时,求证:
时,求证:
①当 时,
时,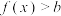 ;
;
②函数 有唯一极值点;
有唯一极值点;
(2)若曲线 与曲线
与曲线 在某公共点处的切线重合,则称该切线为
在某公共点处的切线重合,则称该切线为 和
和 的“优切线”.若曲线
的“优切线”.若曲线 与曲线
与曲线 存在两条互相垂直的“优切线”,求
存在两条互相垂直的“优切线”,求 ,
, 的值.
的值.
 .
.(1)当
 时,求证:
时,求证:①当
 时,
时,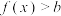 ;
;②函数
 有唯一极值点;
有唯一极值点;(2)若曲线
 与曲线
与曲线 在某公共点处的切线重合,则称该切线为
在某公共点处的切线重合,则称该切线为 和
和 的“优切线”.若曲线
的“优切线”.若曲线 与曲线
与曲线 存在两条互相垂直的“优切线”,求
存在两条互相垂直的“优切线”,求 ,
, 的值.
的值.
您最近一年使用:0次
2024-01-18更新
|
1292次组卷
|
2卷引用:北京市海淀区2024届高三上学期期末练习数学试题
2024高三上·全国·专题练习
5 . 已知函数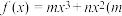 、
、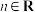 ,
,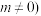 的图象在
的图象在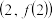 处的切线与
处的切线与 轴平行.
轴平行.
(1)求 ,
, 的关系式并求
的关系式并求 的单调减区间;
的单调减区间;
(2)证明:对任意实数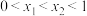 ,关于
,关于 的方程:
的方程: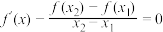 在
在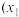 ,
,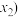 恒有实数解;
恒有实数解;
(3)结合(2)的结论,其实我们有拉格朗日中值定理:若函数 是在闭区间
是在闭区间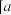 ,
,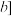 上连续不断的函数,且在区间
上连续不断的函数,且在区间 内导数都存在,则在
内导数都存在,则在 内至少存在一点
内至少存在一点 ,使得
,使得 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
当 时,
时,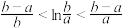 (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性).
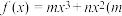 、
、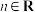 ,
,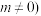 的图象在
的图象在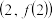 处的切线与
处的切线与 轴平行.
轴平行.(1)求
 ,
, 的关系式并求
的关系式并求 的单调减区间;
的单调减区间;(2)证明:对任意实数
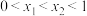 ,关于
,关于 的方程:
的方程: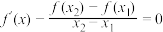 在
在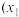 ,
,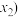 恒有实数解;
恒有实数解;(3)结合(2)的结论,其实我们有拉格朗日中值定理:若函数
 是在闭区间
是在闭区间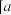 ,
,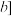 上连续不断的函数,且在区间
上连续不断的函数,且在区间 内导数都存在,则在
内导数都存在,则在 内至少存在一点
内至少存在一点 ,使得
,使得 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:当
 时,
时,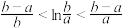 (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性).
您最近一年使用:0次
2024·全国·模拟预测
6 . 如果有且仅有两条不同的直线与函数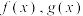 的图象均相切,那么称这两个函数
的图象均相切,那么称这两个函数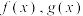 为“
为“ 函数组”.
函数组”.
(1)判断函数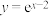 与
与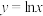 是否为“
是否为“ 函数组”,其中
函数组”,其中 为自然对数的底数,并说明理由;
为自然对数的底数,并说明理由;
(2)已知函数 与
与 为“
为“ 函数组”,求实数
函数组”,求实数 的取值范围.
的取值范围.
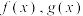 的图象均相切,那么称这两个函数
的图象均相切,那么称这两个函数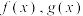 为“
为“ 函数组”.
函数组”.(1)判断函数
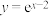 与
与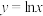 是否为“
是否为“ 函数组”,其中
函数组”,其中 为自然对数的底数,并说明理由;
为自然对数的底数,并说明理由;(2)已知函数
 与
与 为“
为“ 函数组”,求实数
函数组”,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
7 . 设函数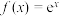 (e为自然对数的底数),函数
(e为自然对数的底数),函数 与函数
与函数 的图象关于直线
的图象关于直线 对称.
对称.
(1)设函数 ,若
,若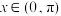 时,
时, 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(2)证明: 与
与 有且仅有两条公切线,且
有且仅有两条公切线,且 图象上两切点横坐标互为相反数.
图象上两切点横坐标互为相反数.
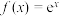 (e为自然对数的底数),函数
(e为自然对数的底数),函数 与函数
与函数 的图象关于直线
的图象关于直线 对称.
对称.(1)设函数
 ,若
,若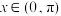 时,
时, 恒成立,求m的取值范围;
恒成立,求m的取值范围;(2)证明:
 与
与 有且仅有两条公切线,且
有且仅有两条公切线,且 图象上两切点横坐标互为相反数.
图象上两切点横坐标互为相反数.
您最近一年使用:0次
2024-01-08更新
|
526次组卷
|
2卷引用:广东省广州市广东实验中学2024届高三上学期大湾区数学冲刺卷(一)
名校
解题方法
8 . (1)已知函数 及其导函数
及其导函数 的定义域均为
的定义域均为 ,设
,设 是曲线
是曲线 在点
在点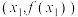 处的切线的方程. 证明:当
处的切线的方程. 证明:当 是增函数时,
是增函数时,
(2)已知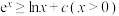 ,设
,设 的最大值为
的最大值为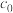 ,证明:
,证明: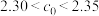 .
.
(参考数据: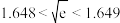 ,
,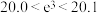 ,
, )
)
 及其导函数
及其导函数 的定义域均为
的定义域均为 ,设
,设 是曲线
是曲线 在点
在点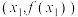 处的切线的方程. 证明:当
处的切线的方程. 证明:当 是增函数时,
是增函数时,
(2)已知
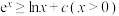 ,设
,设 的最大值为
的最大值为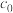 ,证明:
,证明: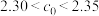 .
.(参考数据:
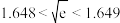 ,
,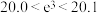 ,
, )
)
您最近一年使用:0次
名校
解题方法
9 . 若函数 在定义域内存在两个不同的数
在定义域内存在两个不同的数 ,
, ,同时满足
,同时满足 ,且
,且 在点
在点 ,
,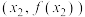 处的切线斜率相同,则称
处的切线斜率相同,则称 为“切合函数”.
为“切合函数”.
(1)证明: 为“切合函数”;
为“切合函数”;
(2)若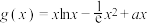 为“切合函数”(其中
为“切合函数”(其中 为自然对数的底数),并设满足条件的两个数为
为自然对数的底数),并设满足条件的两个数为 ,
, .
.
(ⅰ)求证: ;
;
(ⅱ)求证: .
.
 在定义域内存在两个不同的数
在定义域内存在两个不同的数 ,
, ,同时满足
,同时满足 ,且
,且 在点
在点 ,
,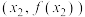 处的切线斜率相同,则称
处的切线斜率相同,则称 为“切合函数”.
为“切合函数”.(1)证明:
 为“切合函数”;
为“切合函数”;(2)若
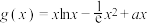 为“切合函数”(其中
为“切合函数”(其中 为自然对数的底数),并设满足条件的两个数为
为自然对数的底数),并设满足条件的两个数为 ,
, .
.(ⅰ)求证:
 ;
;(ⅱ)求证:
 .
.
您最近一年使用:0次
2024-01-03更新
|
1036次组卷
|
4卷引用:重庆市南开中学校2024届高三上学期第五次质量检测数学试题
重庆市南开中学校2024届高三上学期第五次质量检测数学试题重庆市沙坪坝区南开中学校2024届高三上学期第五次质量检测数学试题江西省赣州市南康中学2024届高三上学期新高考“七省联考”考前数学猜题卷(一)(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编
10 . 对于函数 ,分别在
,分别在 处作函数
处作函数 的切线,记切线与
的切线,记切线与 轴的交点分别为
轴的交点分别为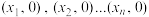 ,记
,记 为数列
为数列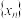 的第n项,则称数列
的第n项,则称数列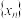 为函数
为函数 的“切线-
的“切线- 轴数列”,同理记切线与
轴数列”,同理记切线与 轴的交点分别为
轴的交点分别为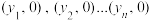 ,记
,记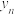 为数列
为数列 的第n项,则称数列
的第n项,则称数列 为函数
为函数 的“切线-
的“切线- 轴数列”
轴数列”
(1)设函数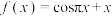 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,记
,记 为
为 的前n项和,求
的前n项和,求 .
.
(2)设函数 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,猜想
,猜想 的通项公式并证明你的结论.
的通项公式并证明你的结论.
(3)设复数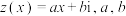 均为不为0的实数,记
均为不为0的实数,记 为
为 的共轭复数,设
的共轭复数,设 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,求证:对于任意的不为0的实数
,求证:对于任意的不为0的实数 ,总有
,总有 成立.
成立.
 ,分别在
,分别在 处作函数
处作函数 的切线,记切线与
的切线,记切线与 轴的交点分别为
轴的交点分别为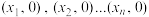 ,记
,记 为数列
为数列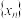 的第n项,则称数列
的第n项,则称数列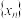 为函数
为函数 的“切线-
的“切线- 轴数列”,同理记切线与
轴数列”,同理记切线与 轴的交点分别为
轴的交点分别为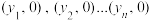 ,记
,记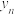 为数列
为数列 的第n项,则称数列
的第n项,则称数列 为函数
为函数 的“切线-
的“切线- 轴数列”
轴数列”(1)设函数
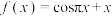 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,记
,记 为
为 的前n项和,求
的前n项和,求 .
.(2)设函数
 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,猜想
,猜想 的通项公式并证明你的结论.
的通项公式并证明你的结论.(3)设复数
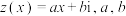 均为不为0的实数,记
均为不为0的实数,记 为
为 的共轭复数,设
的共轭复数,设 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,求证:对于任意的不为0的实数
,求证:对于任意的不为0的实数 ,总有
,总有 成立.
成立.
您最近一年使用:0次
2024-01-01更新
|
443次组卷
|
7卷引用:模块一专题1【练】《导数的概念、运算及其几何意义》单元检测篇B提升卷(人教A2019版)
(已下线)模块一专题1【练】《导数的概念、运算及其几何意义》单元检测篇B提升卷(人教A2019版)(已下线)模块二 专题1 与曲线的切线相关问题(已下线)模块二 专题3 与曲线的切线相关问题(人教B版)(已下线)模块一 专题1 《导数的概念、运算及其几何意义》B提升卷(苏教版)(已下线)模块二 专题1 与曲线的切线相关问题(苏教版高二)(已下线)模块二 专题4 与曲线的切线相关问题(高二北师大版)上海市普陀区桃浦中学2022-2023学年高二下学期期中数学试题



