北京人大附中2021-2022年高一上学期期中数学试题
北京
高一
期中
2021-11-10
1212次
整体难度:
容易
考查范围:
集合与常用逻辑用语、等式与不等式、函数与导数
一、单选题 添加题型下试题
 成立的必要不充分条件有( )
成立的必要不充分条件有( )A.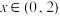 | B.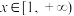 | C.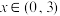 | D. |
 在
在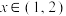 内近似解的过程中,设
内近似解的过程中,设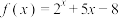 ,且计算
,且计算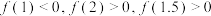 ,则该同学在下次应计算的函数值为( )
,则该同学在下次应计算的函数值为( )A.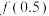 | B.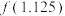 | C.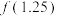 | D.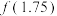 |
【知识点】 二分法求函数零点的过程
 、
、 、
、 、
、 为实数,满足
为实数,满足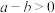 ,
,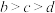 ,
,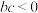 ,则下列不等式正确的是( )
,则下列不等式正确的是( )A. | B.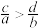 | C.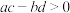 | D. |
 的解集是
的解集是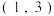 ,则
,则 的值是( )
的值是( )A. | B.3 | C. | D.5 |
【知识点】 由一元二次不等式的解确定参数解读
| A.11元 | B.12元 | C.13元 | D.14元 |
【知识点】 利用给定函数模型解决实际问题
 时,不等式
时,不等式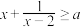 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
【知识点】 基本不等式的恒成立问题解读
 上的奇函数,
上的奇函数, 满足
满足 ,当
,当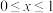 时,
时,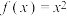 ,则
,则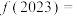 ( )
( )A. | B. | C. | D. |
【知识点】 函数奇偶性的应用 函数的周期性的定义与求解 由函数的周期性求函数值
 是偶函数,且
是偶函数,且 、
、 都有
都有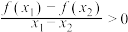 ,若
,若 ,则不等式
,则不等式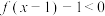 的解集为( )
的解集为( )A.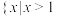 或 或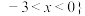 | B. 或 或 |
C. 或 或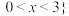 | D. |
二、填空题 添加题型下试题
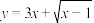 的值域是
的值域是【知识点】 具体函数的定义域解读 利用函数单调性求最值或值域解读
 ,若命题“
,若命题“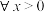 ,都有
,都有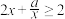 成立”为假命题,则
成立”为假命题,则 的取值范围是
的取值范围是 ,
,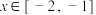 外,再写出一个定义域和值域均为
外,再写出一个定义域和值域均为 的函数:
的函数:【知识点】 待定系数法
| 等级项目 | 优秀 | 合格 | 合计 |
| 除草 | 30 | 15 | 45 |
| 植树 | 20 | 25 | 45 |
【知识点】 容斥原理的应用
三、解答题 添加题型下试题
 ,
, ,
, .
.(1)若
 ,
, 有且只有一个为真命题,求实数
有且只有一个为真命题,求实数 的取值范围;
的取值范围;(2)若
 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
【知识点】 已知命题的真假求参数 根据充分不必要条件求参数解读
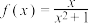 .
.(1)判断并证明函数
 的奇偶性;
的奇偶性;(2)判断当
 时函数
时函数 的单调性,并用定义证明;
的单调性,并用定义证明;(3)若
 定义域为
定义域为 ,解不等式
,解不等式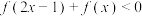 .
.
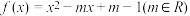 .
.(1)若
 是偶函数,求m的值;
是偶函数,求m的值;(2)函数在区间
 上的最小值记为
上的最小值记为 ,求
,求 的最大值;
的最大值;(3)若函数
 在
在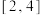 上是单调增函数,求实数m的取值范围.
上是单调增函数,求实数m的取值范围.
四、单选题 添加题型下试题
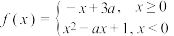 是
是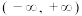 上的减函数,则实数
上的减函数,则实数 的取值范围是( )
的取值范围是( )A.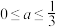 | B. |
C. | D. |
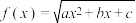 的定义域与值域均为
的定义域与值域均为 ,则
,则 ( )
( )A. | B. | C. | D.1 |
【知识点】 根据值域求参数的值或者范围解读 已知函数的定义域求参数解读
 ,则下列结论中
,则下列结论中A. 的图象关于点 的图象关于点 对称 对称 |
B. 在其定义域上单调递增 在其定义域上单调递增 |
C. 的值域为 的值域为 |
D.函数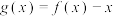 有且只有一个零点 有且只有一个零点 |
五、填空题 添加题型下试题
 ,若对任意的
,若对任意的 ,总有
,总有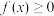 ,则
,则 的范围是
的范围是【知识点】 一次函数的图像和性质 解不含参数的一元二次不等式解读
 ,函数
,函数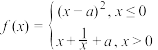 ,若函数
,若函数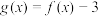 有且仅有3个零点,则a的取值范围是
有且仅有3个零点,则a的取值范围是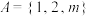 ,其中
,其中 为实数,令
为实数,令 ,
,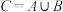 ,若
,若 中的所有元素之和为6,
中的所有元素之和为6, 中的所有元素之积为
中的所有元素之积为【知识点】 判断元素与集合的关系解读 根据并集结果求集合或参数解读
六、解答题 添加题型下试题
 的图象过点
的图象过点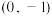 ,且满足
,且满足 .
.(1)求函数
 的解析式;
的解析式;(2)求函数
 在
在 上的最小值;
上的最小值;(3)若
 满足
满足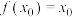 ,则称
,则称 为函数
为函数 的不动点.函数
的不动点.函数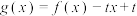 有两个不相等的不动点
有两个不相等的不动点 ,
, ,且
,且 ,
, ,求
,求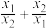 的最小值.
的最小值.
试卷分析
导出试卷题型(共 25题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.85 | 交并补混合运算 | |
| 2 | 0.85 | 判断命题的必要不充分条件 解不含参数的一元二次不等式 | |
| 3 | 0.85 | 二分法求函数零点的过程 | |
| 4 | 0.85 | 由已知条件判断所给不等式是否正确 作差法比较代数式的大小 | |
| 5 | 0.85 | 由一元二次不等式的解确定参数 | |
| 6 | 0.85 | 利用给定函数模型解决实际问题 | |
| 7 | 0.85 | 基本不等式的恒成立问题 | |
| 8 | 0.94 | 求函数值 | |
| 9 | 0.85 | 函数奇偶性的应用 函数的周期性的定义与求解 由函数的周期性求函数值 | |
| 10 | 0.65 | 函数基本性质的综合应用 定义法判断或证明函数的单调性 根据函数的单调性解不等式 由函数奇偶性解不等式 | |
| 19 | 0.85 | 根据函数的单调性求参数值 已知二次函数单调区间求参数值或范围 根据分段函数的单调性求参数 | |
| 20 | 0.65 | 根据值域求参数的值或者范围 已知函数的定义域求参数 | |
| 21 | 0.85 | 函数奇偶性的应用 判断或证明函数的对称性 求函数零点或方程根的个数 根据解析式直接判断函数的单调性 | |
| 二、填空题 | |||
| 11 | 0.85 | 具体函数的定义域 利用函数单调性求最值或值域 | 单空题 |
| 12 | 0.65 | 根据特称(存在性)命题的真假求参数 函数不等式能成立(有解)问题 | 单空题 |
| 13 | 0.65 | 待定系数法 | 单空题 |
| 14 | 0.65 | 函数与方程的综合应用 求函数的零点 | 单空题 |
| 15 | 0.85 | 容斥原理的应用 | 单空题 |
| 22 | 0.65 | 一次函数的图像和性质 解不含参数的一元二次不等式 | 单空题 |
| 23 | 0.65 | 函数图象的应用 根据函数零点的个数求参数范围 基本不等式求和的最小值 | 单空题 |
| 24 | 0.4 | 判断元素与集合的关系 根据并集结果求集合或参数 | 单空题 |
| 三、解答题 | |||
| 16 | 0.65 | 已知命题的真假求参数 根据充分不必要条件求参数 | 问答题 |
| 17 | 0.85 | 定义法判断或证明函数的单调性 函数奇偶性的定义与判断 根据函数的单调性解不等式 由函数奇偶性解不等式 | 证明题 |
| 18 | 0.4 | 求二次函数的值域或最值 已知二次函数单调区间求参数值或范围 分段函数的值域或最值 由奇偶性求参数 | 问答题 |
| 25 | 0.4 | 求二次函数的值域或最值 求二次函数的解析式 根据二次函数零点的分布求参数的范围 基本不等式求和的最小值 | 问答题 |

 ,集合
,集合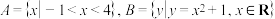 ,则
,则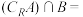 (
(


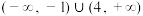
 ,
,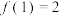 ,则
,则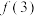 等于(
等于( 表示不大于
表示不大于 的零点为
的零点为

