贵州省贵阳市观山湖区第一高级中学2023-2024学年高二上学期9月月考数学试题
贵州
高二
阶段练习
2023-10-27
244次
整体难度:
容易
考查范围:
空间向量与立体几何、平面解析几何、平面向量、等式与不等式、复数
一、单选题 添加题型下试题
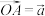 ,
,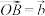 ,
,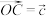 ,点M在OA上,且,M为OA中点,N为BC中点,则
,点M在OA上,且,M为OA中点,N为BC中点,则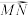 等于( )
等于( )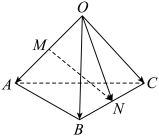
A.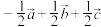 | B.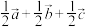 |
C.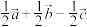 | D.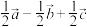 |
【知识点】 空间向量加减运算的几何表示 空间向量数乘运算的几何表示
 的底面
的底面 是矩形,
是矩形, ,
,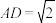 ,
,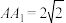 ,且
,且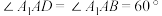 ,则线段
,则线段 的长为( )
的长为( )
A. | B.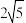 | C.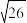 | D.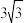 |
【知识点】 空间向量数量积的应用
 过点
过点 ,且与向量
,且与向量 平行,则直线
平行,则直线 在
在 轴上的截距为( )
轴上的截距为( )A. | B. | C. | D. |
【知识点】 直线截距式方程及辨析 根据直线的方向向量求直线方程
 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列说法正确的是( )
是两个不同的平面,则下列说法正确的是( )A.若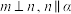 ,则 ,则 |
B.若 ,则 ,则 |
C.若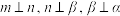 ,则 ,则 |
D.若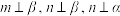 ,则 ,则 |
【知识点】 线面关系有关命题的判断 面面关系有关命题的判断
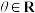 ,则直线
,则直线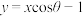 的倾斜角
的倾斜角 的取值范围为( )
的取值范围为( )A.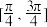 | B. |
C.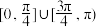 | D.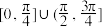 |
【知识点】 直线的倾斜角 斜率与倾斜角的变化关系
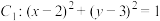 ,圆
,圆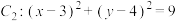 ,M,N分别是圆
,M,N分别是圆 上的动点,P为x轴上的动点,则
上的动点,P为x轴上的动点,则 的最小值为( )
的最小值为( )A.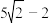 | B.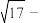 1 1 | C.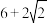 | D.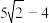 |
【知识点】 圆上点到定直线(图形)上的最值(范围)
 :
: (
( )和两点
)和两点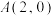 ,
, .若圆
.若圆 上存在四个不同的点
上存在四个不同的点 ,使得
,使得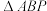 的面积为
的面积为 ,则
,则 的取值范围是( )
的取值范围是( )A. | B.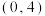 | C.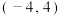 | D. |
【知识点】 由直线与圆的位置关系求参数
二、多选题 添加题型下试题
A.已知点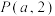 , ,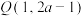 ,若直线 ,若直线 的倾斜角小于 的倾斜角小于 ,则实数a的取值范围为 ,则实数a的取值范围为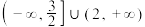 |
B.若集合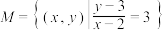 , ,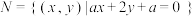 满足 满足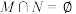 ,则 ,则 |
C.若两条平行直线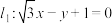 和 和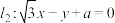 之间的距离小于1,则实数a的取值范围为 之间的距离小于1,则实数a的取值范围为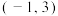 |
D.若直线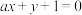 与连接 与连接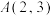 , , 的线段相交,则实数a的取值范围为 的线段相交,则实数a的取值范围为 |
【知识点】 直线的倾斜角 直线过定点问题 求平行线间的距离 直线与线段的相交关系求斜率范围
 的棱长为1,点
的棱长为1,点 分别是
分别是 的中点,
的中点, 在正方体内部且满足
在正方体内部且满足 ,则下列说法正确的是( )
,则下列说法正确的是( )A.点 到直线 到直线 的距离是 的距离是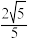 | B.点 到平面 到平面 的距离为 的距离为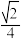 |
C.点 到直线 到直线 的距离为 的距离为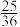 | D.平面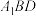 与平面 与平面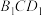 间的距离为 间的距离为 |
【知识点】 空间平行的转化 点到平面距离的向量求法 点到直线距离的向量求法
 :
: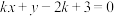 ,
, :
: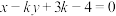 ,设两直线分别过定点
,设两直线分别过定点 ,
, ,直线
,直线 和直线
和直线 的交点为
的交点为 ,则下列结论正确的有( )
,则下列结论正确的有( )A.直线 过定点 过定点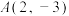 ,直线 ,直线 过定点 过定点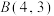 |
B.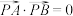 |
C. 面积的最大值为5 面积的最大值为5 |
D.若 , ,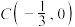 ,则点 ,则点 恒满足 恒满足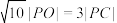 |
 中,底面
中,底面 是边长为1的正方形.
是边长为1的正方形. 底面
底面 ,
,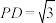 ,点E是棱PB上一点(不包括端点).F是平面PCD内一点,则( )
,点E是棱PB上一点(不包括端点).F是平面PCD内一点,则( )
A.一定存在点E,使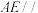 平面PCD 平面PCD |
B.一定存在点E,使 平面ACE 平面ACE |
C. 的最小值为 的最小值为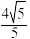 |
D.以D为球心,半径为1的球与四棱锥 的四个侧面的交线长为 的四个侧面的交线长为 |
【知识点】 棱锥的展开图 球的截面的性质及计算 证明线面垂直 空间位置关系的向量证明
三、填空题 添加题型下试题
 过点
过点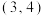 ,且在
,且在 轴上的截距是在
轴上的截距是在 轴上的截距的两倍,则直线
轴上的截距的两倍,则直线 的方程为
的方程为【知识点】 直线的点斜式方程及辨析 直线截距式方程及辨析
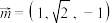 ,若点
,若点 为直线l外一点,
为直线l外一点,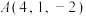 为直线l上一点,则点P到直线l的距离为
为直线l上一点,则点P到直线l的距离为【知识点】 点到直线距离的向量求法
 ,则
,则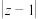 的最大值是
的最大值是  的棱长为
的棱长为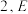 是棱
是棱 的中点,则平面
的中点,则平面 截该正方体所得的截面面积为
截该正方体所得的截面面积为【知识点】 正棱柱及其有关计算 判断正方体的截面形状 由平面的基本性质作截面图形
四、解答题 添加题型下试题
 中,
中,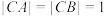 ,
,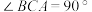 ,棱
,棱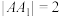 ,点
,点 、
、 分别是
分别是 、
、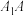 的中点.建立适当的空间直角坐标系,解决如下问题:
的中点.建立适当的空间直角坐标系,解决如下问题: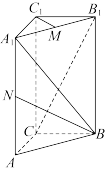
(1)求
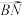 的模;
的模;(2)求
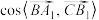 ;
;(3)求证:
 .
.
 的顶点为
的顶点为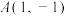 ,
,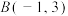 ,
,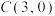 ,AD是BC边上的高,AE是
,AD是BC边上的高,AE是 的平分线.
的平分线.
(2)求AE所在直线的方程.(提示:在
 上取与
上取与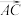 长度相等的向量
长度相等的向量 ,则
,则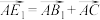 的方向就是
的方向就是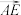 的方向.)
的方向.)
20. 已知坐标平面上点 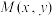 与两个定点
与两个定点 的距离之比等于 2 .
的距离之比等于 2 .
(1)求点
 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为
 ,过点
,过点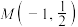 的直线
的直线 被
被 所截得的线段的长为
所截得的线段的长为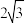 ,求直线
,求直线 的方程.
的方程.
【知识点】 轨迹问题——圆 已知圆的弦长求方程或参数
 中,
中, 平面
平面 ,
, ,
, ,
,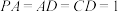 ,
, ,点
,点 是
是 的中点.
的中点.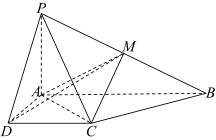
 ;
;(2)求直线
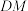 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.
【知识点】 求线面角 线面垂直证明线线垂直
 中,
中, ,
,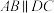 ,
, 是
是 的中点,
的中点, 平面
平面 ,
,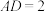 ,
, ,
, .
.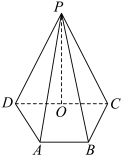
(1)求点
 到平面
到平面 的距离;
的距离;(2)在线段
 上是否存在一点
上是否存在一点 ,使二面角
,使二面角 的余弦值为
的余弦值为 ?若存在,请确定点
?若存在,请确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【知识点】 已知面面角求其他量 点到平面距离的向量求法
试卷分析
导出试卷题型(共 22题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.85 | 空间向量加减运算的几何表示 空间向量数乘运算的几何表示 | |
| 2 | 0.65 | 空间向量数量积的应用 | |
| 3 | 0.85 | 已知直线平行求参数 已知直线垂直求参数 | |
| 4 | 0.85 | 直线截距式方程及辨析 根据直线的方向向量求直线方程 | |
| 5 | 0.85 | 线面关系有关命题的判断 面面关系有关命题的判断 | |
| 6 | 0.85 | 直线的倾斜角 斜率与倾斜角的变化关系 | |
| 7 | 0.65 | 圆上点到定直线(图形)上的最值(范围) | |
| 8 | 0.65 | 由直线与圆的位置关系求参数 | |
| 二、多选题 | |||
| 9 | 0.65 | 直线的倾斜角 直线过定点问题 求平行线间的距离 直线与线段的相交关系求斜率范围 | |
| 10 | 0.65 | 空间平行的转化 点到平面距离的向量求法 点到直线距离的向量求法 | |
| 11 | 0.65 | 垂直关系的向量表示 基本不等式求积的最大值 直线过定点问题 轨迹问题——圆 | |
| 12 | 0.4 | 棱锥的展开图 球的截面的性质及计算 证明线面垂直 空间位置关系的向量证明 | |
| 三、填空题 | |||
| 13 | 0.85 | 直线的点斜式方程及辨析 直线截距式方程及辨析 | 单空题 |
| 14 | 0.85 | 点到直线距离的向量求法 | 单空题 |
| 15 | 0.65 | 定点到圆上点的最值(范围) 与复数模相关的轨迹(图形)问题 | 单空题 |
| 16 | 0.65 | 正棱柱及其有关计算 判断正方体的截面形状 由平面的基本性质作截面图形 | 单空题 |
| 四、解答题 | |||
| 17 | 0.85 | 求空间图形上的点的坐标 空间向量模长的坐标表示 空间位置关系的向量证明 异面直线夹角的向量求法 | 证明题 |
| 18 | 0.65 | 平面向量线性运算的坐标表示 已知直线垂直求参数 直线的点斜式方程及辨析 求直线的方向向量 | 问答题 |
| 19 | 0.85 | 证明线面平行 证明线面垂直 | 证明题 |
| 20 | 0.65 | 轨迹问题——圆 已知圆的弦长求方程或参数 | 问答题 |
| 21 | 0.65 | 求线面角 线面垂直证明线线垂直 | 问答题 |
| 22 | 0.65 | 已知面面角求其他量 点到平面距离的向量求法 | 问答题 |

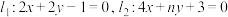 ,
,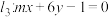 ,若
,若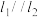 且
且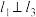 ,则
,则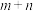 的值为(
的值为(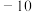


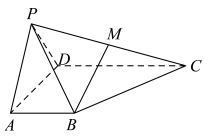
 的中点,
的中点,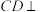 平面
平面 ,
,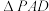 为等边三角形,
为等边三角形,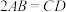 .
.
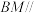 平面
平面 平面
平面 .
.


