名校
1 . 定义域为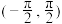 的函数
的函数 满足
满足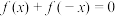 ,其导函数为
,其导函数为 ,当
,当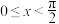 时,有
时,有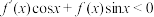 成立,则关于x的不等式
成立,则关于x的不等式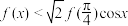 的解集为( )
的解集为( )
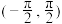 的函数
的函数 满足
满足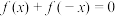 ,其导函数为
,其导函数为 ,当
,当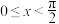 时,有
时,有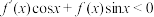 成立,则关于x的不等式
成立,则关于x的不等式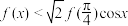 的解集为( )
的解集为( )A.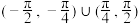 | B.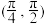 |
C.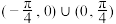 | D.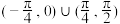 |
您最近半年使用:0次
2 . 若定义在R上的函数 满足
满足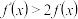 ,则当
,则当 时,
时,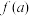 与
与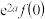 的大小关系为( )
的大小关系为( )
 满足
满足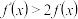 ,则当
,则当 时,
时,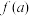 与
与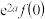 的大小关系为( )
的大小关系为( )A.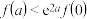 | B.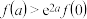 |
C.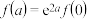 | D.不能确定 |
您最近半年使用:0次
名校
3 . 定义在 上的偶函数
上的偶函数 的导函数满足
的导函数满足 ,且
,且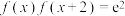 ,若
,若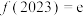 ,则不等式
,则不等式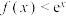 的解集为
的解集为_______ .
 上的偶函数
上的偶函数 的导函数满足
的导函数满足 ,且
,且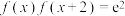 ,若
,若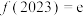 ,则不等式
,则不等式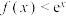 的解集为
的解集为
您最近半年使用:0次
名校
4 . 已知函数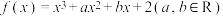 的图象在点
的图象在点 处的切线方程为
处的切线方程为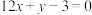 .
.
(1)求函数 的单调区间;
的单调区间;
(2)求 在
在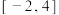 的最值.
的最值.
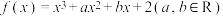 的图象在点
的图象在点 处的切线方程为
处的切线方程为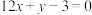 .
.(1)求函数
 的单调区间;
的单调区间;(2)求
 在
在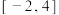 的最值.
的最值.
您最近半年使用:0次
2024-04-20更新
|
343次组卷
|
2卷引用:广东省广州市番禺区大龙中学2023-2024学年高二下学期3月月考数学试卷
名校
5 . 设函数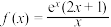 ,则( )
,则( )
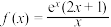 ,则( )
,则( )A.函数 的单调递减区间为 的单调递减区间为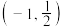 . . |
B.曲线 在点 在点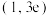 处的切线方程为 处的切线方程为 . . |
C.函数 既有极大值又有极小值,且极大值小于极小值. 既有极大值又有极小值,且极大值小于极小值. |
D.若方程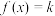 有两个不等实根,则实数k的取值范围为 有两个不等实根,则实数k的取值范围为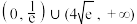 |
您最近半年使用:0次
2024-04-20更新
|
508次组卷
|
3卷引用:江苏省常州市北郊高级中学2023-2024学年高二下学期3月阶段调研数学试卷
名校
解题方法
6 . 若函数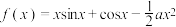 在
在 上单调递增,则
上单调递增,则 的最大值为
的最大值为______ .
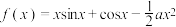 在
在 上单调递增,则
上单调递增,则 的最大值为
的最大值为
您最近半年使用:0次
2024-04-19更新
|
413次组卷
|
2卷引用:河北省邢台市名校联盟2023-2024学年高二下学期质检联盟第一次月考(3月)数学试题
解题方法
7 . 已知x,y为正实数,则可成为“ ”的充要条件的是( )
”的充要条件的是( )
 ”的充要条件的是( )
”的充要条件的是( )A.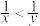 | B.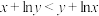 |
C.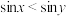 | D. |
您最近半年使用:0次
8 . 已知函数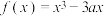
(1)若 ,求函数的严格减区间
,求函数的严格减区间
(2)若方程 在实数集上有四个解,求实数
在实数集上有四个解,求实数 的取值范围
的取值范围
(3)若 ,数列
,数列 满足
满足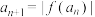 .是否存在
.是否存在 使得数列
使得数列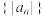 严格递减?存在的话.求出所有这样的
严格递减?存在的话.求出所有这样的 ;不存在的话.说明理由
;不存在的话.说明理由
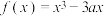
(1)若
 ,求函数的严格减区间
,求函数的严格减区间(2)若方程
 在实数集上有四个解,求实数
在实数集上有四个解,求实数 的取值范围
的取值范围(3)若
 ,数列
,数列 满足
满足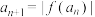 .是否存在
.是否存在 使得数列
使得数列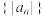 严格递减?存在的话.求出所有这样的
严格递减?存在的话.求出所有这样的 ;不存在的话.说明理由
;不存在的话.说明理由
您最近半年使用:0次
解题方法
9 . 曲线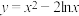 的单调增区间是( )
的单调增区间是( )
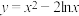 的单调增区间是( )
的单调增区间是( )A. | B. | C.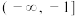 和 和 | D.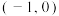 和 和 |
您最近半年使用:0次
名校
10 . 已知函数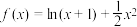 ,
, .
.
(1)求 的单调区间;
的单调区间;
(2)若对于正实数 ,满足
,满足 .
.
(i)证明: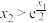 ;
;
(ii)证明: .
.
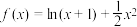 ,
, .
.(1)求
 的单调区间;
的单调区间;(2)若对于正实数
 ,满足
,满足 .
.(i)证明:
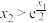 ;
;(ii)证明:
 .
.
您最近半年使用:0次



