解题方法
1 . 已知正方形ABCD的顶点均在表面积为 的球O的球面上,则当四棱锥
的球O的球面上,则当四棱锥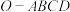 的体积取得最大值时,点O到平面ABCD的距离为( )
的体积取得最大值时,点O到平面ABCD的距离为( )
 的球O的球面上,则当四棱锥
的球O的球面上,则当四棱锥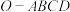 的体积取得最大值时,点O到平面ABCD的距离为( )
的体积取得最大值时,点O到平面ABCD的距离为( )A. | B. | C. | D.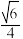 |
您最近一年使用:0次
今日更新
|
4次组卷
|
2卷引用:陕西省铜川市王益中学2024届高三下学期高考猜题信息卷(二)文科数学试题
名校
解题方法
2 . 已知函数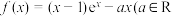 且
且 为常数).
为常数).
(1)当 ,求函数
,求函数 的最小值;
的最小值;
(2)若函数 有2个极值点,求
有2个极值点,求 的取值范围;
的取值范围;
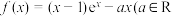 且
且 为常数).
为常数).(1)当
 ,求函数
,求函数 的最小值;
的最小值;(2)若函数
 有2个极值点,求
有2个极值点,求 的取值范围;
的取值范围;
您最近一年使用:0次
2024高二下·全国·专题练习
3 . 设函数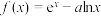 .
.
(1)当 ,求
,求 在点
在点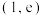 处的切线方程;
处的切线方程;
(2)证明:当 时,
时,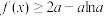 ;
;
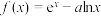 .
.(1)当
 ,求
,求 在点
在点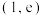 处的切线方程;
处的切线方程;(2)证明:当
 时,
时,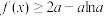 ;
;
您最近一年使用:0次
昨日更新
|
255次组卷
|
3卷引用:专题4 利用导数解决不等式证明问题【练】(高二期末压轴专项)
(已下线)专题4 利用导数解决不等式证明问题【练】(高二期末压轴专项)湖南省益阳市安化县两校联考2023-2024学年高二下学期7月期末自检数学试题湖南省永州市名校联盟2023-2024学年高二下学期期末考试数学试题
解题方法
4 . 函数 的定义域为
的定义域为 ,导函数
,导函数 在
在 内的图象如图所示,则( )
内的图象如图所示,则( )
 的定义域为
的定义域为 ,导函数
,导函数 在
在 内的图象如图所示,则( )
内的图象如图所示,则( )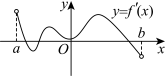
A.函数 在 在 上只有一个极小值点 上只有一个极小值点 |
B.函数 在 在 上有两个极大值点 上有两个极大值点 |
C.函数 在 在 上可能没有零点 上可能没有零点 |
D.函数 在 在 上一定不存在最小值 上一定不存在最小值 |
您最近一年使用:0次
解题方法
5 . 已知函数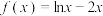 .
.
(1)求函数 的最大值;
的最大值;
(2)若不等式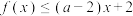 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
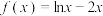 .
.(1)求函数
 的最大值;
的最大值;(2)若不等式
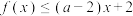 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
6 . 为了解某地区电视观众对某类体育节目的收视情况,某电视传媒公司随机抽取了该地区100名电视观众进行调查,调查数据如下:
(1)完成上面的  列联表,依据
列联表,依据  的独立性检验,能否认为“体育迷”与性别有关联?
的独立性检验,能否认为“体育迷”与性别有关联?
(2)五一期间,该地区电视台在某体育赛事现场直播期间开展电话连线活动,计划从该地区电视观众中随机连线5名观众,假设每位电视观众连线成功的概率均为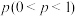 ,各人是否连线成功互不影响,记连线的5名观众中恰有3人连线成功的概率为
,各人是否连线成功互不影响,记连线的5名观众中恰有3人连线成功的概率为 ,求
,求 取得最大值时
取得最大值时 的值.
的值.
附: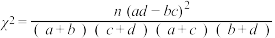 (其中
(其中  )
)
| 非体育迷 | 体育迷 | 合计 | |
| 男 | 30 | 45 | |
| 女 | 10 | ||
| 合计 | 75 | 100 |
 列联表,依据
列联表,依据  的独立性检验,能否认为“体育迷”与性别有关联?
的独立性检验,能否认为“体育迷”与性别有关联?(2)五一期间,该地区电视台在某体育赛事现场直播期间开展电话连线活动,计划从该地区电视观众中随机连线5名观众,假设每位电视观众连线成功的概率均为
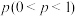 ,各人是否连线成功互不影响,记连线的5名观众中恰有3人连线成功的概率为
,各人是否连线成功互不影响,记连线的5名观众中恰有3人连线成功的概率为 ,求
,求 取得最大值时
取得最大值时 的值.
的值.附:
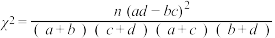 (其中
(其中  )
) | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
解题方法
7 . 已知函数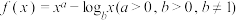 ,若
,若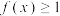 恒成立,则
恒成立,则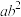 的最小值为( )
的最小值为( )
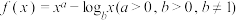 ,若
,若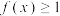 恒成立,则
恒成立,则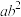 的最小值为( )
的最小值为( )A. | B.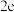 | C.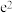 | D. |
您最近一年使用:0次
8 . 已知函数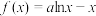 有两个零点,则( )
有两个零点,则( )
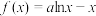 有两个零点,则( )
有两个零点,则( )A. | B.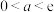 | C. | D. |
您最近一年使用:0次
9 . 已知函数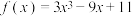 .
.
(1)求曲线 在点
在点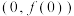 处的切线方程;
处的切线方程;
(2)求曲线 的单调区间及在
的单调区间及在 上的最大值.
上的最大值.
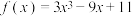 .
.(1)求曲线
 在点
在点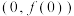 处的切线方程;
处的切线方程;(2)求曲线
 的单调区间及在
的单调区间及在 上的最大值.
上的最大值.
您最近一年使用:0次
10 . 关于函数 ,下列结论中错误的是( )
,下列结论中错误的是( )
 ,下列结论中错误的是( )
,下列结论中错误的是( )A. 定义域为 定义域为 | B. 在 在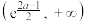 上单调递增 上单调递增 |
C.当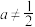 时, 时, | D.当 时, 时, |
您最近一年使用:0次



