1 . 已知椭圆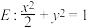 的左、右焦点分别为
的左、右焦点分别为 ,
, ,过点
,过点 的动直线l交E于A,B两点,且点A在x轴上方,直线
的动直线l交E于A,B两点,且点A在x轴上方,直线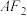 与E交于另一点C,直线
与E交于另一点C,直线 与E于另一点D.
与E于另一点D.
(1)求 的面积最大值;
的面积最大值;
(2)证明:直线CD过定点.
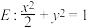 的左、右焦点分别为
的左、右焦点分别为 ,
, ,过点
,过点 的动直线l交E于A,B两点,且点A在x轴上方,直线
的动直线l交E于A,B两点,且点A在x轴上方,直线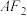 与E交于另一点C,直线
与E交于另一点C,直线 与E于另一点D.
与E于另一点D.(1)求
 的面积最大值;
的面积最大值;(2)证明:直线CD过定点.
您最近一年使用:0次
7日内更新
|
86次组卷
|
3卷引用:云南省昆明市第一中学2024届高三第十次考前适应性训练数学试卷
2 . 如图,矩形 中,
中,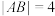 ,
, ,
,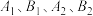 分别是矩形四条边的中点,设
分别是矩形四条边的中点,设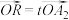 ,
,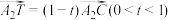 ,设直线
,设直线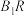 与
与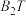 的交点
的交点 在曲线
在曲线 上.
上. 的方程;
的方程;
(2)直线 与曲线
与曲线 交于
交于 ,
, 两点,点
两点,点 在第一象限,点
在第一象限,点 在第四象限,且满足直线
在第四象限,且满足直线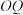 与直线
与直线 的斜率之积为
的斜率之积为 ,若点
,若点 为曲线
为曲线 的左顶点,且满足
的左顶点,且满足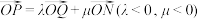 ,直线
,直线 与
与 交于
交于 ,直线
,直线 与
与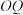 交于
交于 .
.
①证明: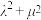 为定值;
为定值;
②是否存在常数 ,使得四边形
,使得四边形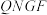 的面积是
的面积是 面积的
面积的 倍?若存在求出
倍?若存在求出 ,若不存在说明理由.
,若不存在说明理由.
 中,
中,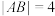 ,
, ,
,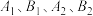 分别是矩形四条边的中点,设
分别是矩形四条边的中点,设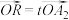 ,
,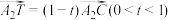 ,设直线
,设直线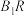 与
与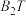 的交点
的交点 在曲线
在曲线 上.
上.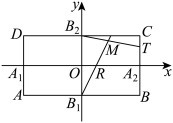
 的方程;
的方程;(2)直线
 与曲线
与曲线 交于
交于 ,
, 两点,点
两点,点 在第一象限,点
在第一象限,点 在第四象限,且满足直线
在第四象限,且满足直线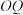 与直线
与直线 的斜率之积为
的斜率之积为 ,若点
,若点 为曲线
为曲线 的左顶点,且满足
的左顶点,且满足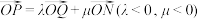 ,直线
,直线 与
与 交于
交于 ,直线
,直线 与
与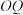 交于
交于 .
.①证明:
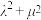 为定值;
为定值;②是否存在常数
 ,使得四边形
,使得四边形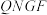 的面积是
的面积是 面积的
面积的 倍?若存在求出
倍?若存在求出 ,若不存在说明理由.
,若不存在说明理由.
您最近一年使用:0次
名校
解题方法
3 . 已知抛物线 ,焦点为
,焦点为 ,点
,点 为曲线
为曲线 的准线与对称轴的交点,过
的准线与对称轴的交点,过 的直线
的直线 与抛物线
与抛物线 交于
交于 两点.
两点.
(1)证明:当 时,
时, 与抛物线相切;
与抛物线相切;
(2)当 时,求
时,求 .
.
 ,焦点为
,焦点为 ,点
,点 为曲线
为曲线 的准线与对称轴的交点,过
的准线与对称轴的交点,过 的直线
的直线 与抛物线
与抛物线 交于
交于 两点.
两点.(1)证明:当
 时,
时, 与抛物线相切;
与抛物线相切;(2)当
 时,求
时,求 .
.
您最近一年使用:0次
名校
解题方法
4 . 英国物理学家、数学家艾萨克·牛顿与德国哲学家、数学家戈特弗里德·莱布尼茨各自独立发明了微积分,其中牛顿在《流数法与无穷级数》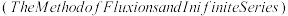 一书中,给出了高次代数方程的一种数值解法——牛顿法.如图,具体做法如下:一个函数的零点为
一书中,给出了高次代数方程的一种数值解法——牛顿法.如图,具体做法如下:一个函数的零点为 ,先在
,先在 轴找初始点
轴找初始点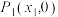 ,然后作
,然后作 在点
在点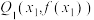 处切线,切线与
处切线,切线与 轴交于点
轴交于点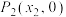 ,再作
,再作 在点
在点 处切线,切线与
处切线,切线与 轴交于点
轴交于点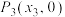 ,再作
,再作 在点
在点 处切线,以此类推,直到求得满足精度
处切线,以此类推,直到求得满足精度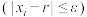 的零点近似解
的零点近似解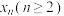 为止.
为止. ,初始点
,初始点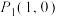 ,精度
,精度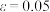 ,若按上述算法,求函数
,若按上述算法,求函数 的零点近似解满足精度时
的零点近似解满足精度时 的最小值(参考数据:
的最小值(参考数据: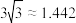 );
);
(2)设函数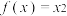 ,令
,令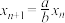 ,且
,且 ,若函数
,若函数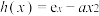 ,
,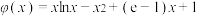 ,证明:当
,证明:当 时,
时,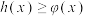 .
.
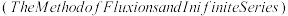 一书中,给出了高次代数方程的一种数值解法——牛顿法.如图,具体做法如下:一个函数的零点为
一书中,给出了高次代数方程的一种数值解法——牛顿法.如图,具体做法如下:一个函数的零点为 ,先在
,先在 轴找初始点
轴找初始点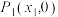 ,然后作
,然后作 在点
在点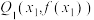 处切线,切线与
处切线,切线与 轴交于点
轴交于点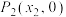 ,再作
,再作 在点
在点 处切线,切线与
处切线,切线与 轴交于点
轴交于点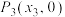 ,再作
,再作 在点
在点 处切线,以此类推,直到求得满足精度
处切线,以此类推,直到求得满足精度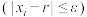 的零点近似解
的零点近似解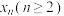 为止.
为止.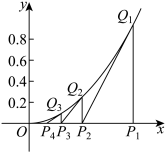
 ,初始点
,初始点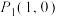 ,精度
,精度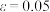 ,若按上述算法,求函数
,若按上述算法,求函数 的零点近似解满足精度时
的零点近似解满足精度时 的最小值(参考数据:
的最小值(参考数据: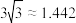 );
);(2)设函数
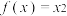 ,令
,令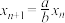 ,且
,且 ,若函数
,若函数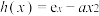 ,
,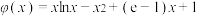 ,证明:当
,证明:当 时,
时,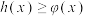 .
.
您最近一年使用:0次
名校
解题方法
5 . 已知函数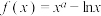 ,
, .
.
(1)求 的最小值
的最小值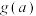 ;
;
(2)证明: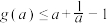 .
.
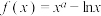 ,
, .
.(1)求
 的最小值
的最小值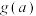 ;
;(2)证明:
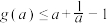 .
.
您最近一年使用:0次
2024-06-09更新
|
129次组卷
|
2卷引用:云南省昆明市第一中学2024届高三第十次考前适应性训练数学试卷
名校
解题方法
6 . 设 是由满足下列条件的函数
是由满足下列条件的函数 构成的集合:①方程
构成的集合:①方程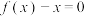 有实根;②
有实根;② 在定义域区间
在定义域区间 上可导,且
上可导,且 满足
满足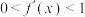 .
.
(1)判断 ,
,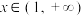 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(2)设函数 为集合
为集合 中的任意一个元素,证明:对其定义域区间
中的任意一个元素,证明:对其定义域区间 中的任意
中的任意 、
、 ,都有
,都有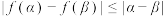 .
.
 是由满足下列条件的函数
是由满足下列条件的函数 构成的集合:①方程
构成的集合:①方程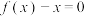 有实根;②
有实根;② 在定义域区间
在定义域区间 上可导,且
上可导,且 满足
满足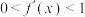 .
.(1)判断
 ,
,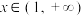 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;(2)设函数
 为集合
为集合 中的任意一个元素,证明:对其定义域区间
中的任意一个元素,证明:对其定义域区间 中的任意
中的任意 、
、 ,都有
,都有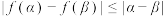 .
.
您最近一年使用:0次
2024-06-08更新
|
392次组卷
|
3卷引用:云南省昆明市第三中学2024届高三下学期高考考前检测数学试卷
解题方法
7 . 已知函数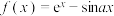 ;
;
(1)当 时,证明:对任意
时,证明:对任意 ,
, ;
;
(2)若 是函数
是函数 的极值点,求实数
的极值点,求实数 的值.
的值.
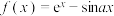 ;
;(1)当
 时,证明:对任意
时,证明:对任意 ,
, ;
;(2)若
 是函数
是函数 的极值点,求实数
的极值点,求实数 的值.
的值.
您最近一年使用:0次
8 . 已知函数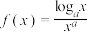 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)证明:若曲线 与直线
与直线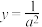 有且仅有两个交点,求
有且仅有两个交点,求 的取值范围.
的取值范围.
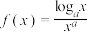 .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)证明:若曲线
 与直线
与直线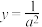 有且仅有两个交点,求
有且仅有两个交点,求 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
9 . 椭圆 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 在椭圆
在椭圆 上运动(与左、右顶点不重合),已知
上运动(与左、右顶点不重合),已知 的内切圆圆心为
的内切圆圆心为 ,延长
,延长 交
交 轴于点
轴于点 .
.
(1)当点 运动到椭圆
运动到椭圆 的上顶点时,求
的上顶点时,求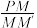 ;
;
(2)当点 在椭圆
在椭圆 上运动时,
上运动时,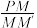 为定值,求
为定值,求 内切圆圆心
内切圆圆心 的轨迹方程;
的轨迹方程;
(3)点 关于
关于 轴对称的点为
轴对称的点为 ,直线
,直线 与
与 相交于点
相交于点 ,已知点
,已知点 的轨迹为
的轨迹为 ,过点
,过点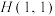 的直线
的直线 与曲线
与曲线 交于
交于 两点,试说明:是否存在直线
两点,试说明:是否存在直线 ,使得点
,使得点 为线段
为线段 的中点,若存在,求出直线
的中点,若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 在椭圆
在椭圆 上运动(与左、右顶点不重合),已知
上运动(与左、右顶点不重合),已知 的内切圆圆心为
的内切圆圆心为 ,延长
,延长 交
交 轴于点
轴于点 .
.(1)当点
 运动到椭圆
运动到椭圆 的上顶点时,求
的上顶点时,求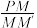 ;
;(2)当点
 在椭圆
在椭圆 上运动时,
上运动时,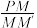 为定值,求
为定值,求 内切圆圆心
内切圆圆心 的轨迹方程;
的轨迹方程;(3)点
 关于
关于 轴对称的点为
轴对称的点为 ,直线
,直线 与
与 相交于点
相交于点 ,已知点
,已知点 的轨迹为
的轨迹为 ,过点
,过点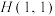 的直线
的直线 与曲线
与曲线 交于
交于 两点,试说明:是否存在直线
两点,试说明:是否存在直线 ,使得点
,使得点 为线段
为线段 的中点,若存在,求出直线
的中点,若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
您最近一年使用:0次
解题方法
10 . 已知函数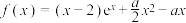 .
.
(1)当 时,求函数
时,求函数 的最小值;
的最小值;
(2)讨论函数 的单调性.
的单调性.
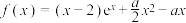 .
.(1)当
 时,求函数
时,求函数 的最小值;
的最小值;(2)讨论函数
 的单调性.
的单调性.
您最近一年使用:0次



