1 . 已知抛物线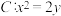 ,动圆
,动圆

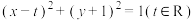 ,
, 为抛物线
为抛物线 上一动点,过点
上一动点,过点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.
(1)若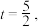 求
求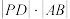 的最小值;
的最小值;
(2)若过圆心 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为 .
.
(Ⅰ)求证:直线 过定点;
过定点;
(Ⅱ)若线段 的中点为
的中点为 ,连
,连 交抛物线
交抛物线 于点
于点 ,记
,记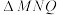 的面积为
的面积为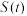 ,求
,求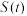 的表达式及其最小值.
的表达式及其最小值.
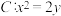 ,动圆
,动圆

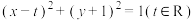 ,
, 为抛物线
为抛物线 上一动点,过点
上一动点,过点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.(1)若
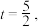 求
求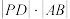 的最小值;
的最小值;(2)若过圆心
 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为 .
.(Ⅰ)求证:直线
 过定点;
过定点;(Ⅱ)若线段
 的中点为
的中点为 ,连
,连 交抛物线
交抛物线 于点
于点 ,记
,记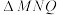 的面积为
的面积为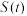 ,求
,求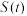 的表达式及其最小值.
的表达式及其最小值.
您最近一年使用:0次
名校
解题方法
2 . 如图,在正四面体 中,已知
中,已知 ,
, 为棱
为棱 的中点. 现将等腰直角三角形
的中点. 现将等腰直角三角形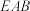 绕其斜边
绕其斜边 旋转一周(假设
旋转一周(假设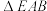 可以穿过正四面体内部),则在旋转过程中,下列结论正确的是( )
可以穿过正四面体内部),则在旋转过程中,下列结论正确的是( )
 中,已知
中,已知 ,
, 为棱
为棱 的中点. 现将等腰直角三角形
的中点. 现将等腰直角三角形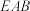 绕其斜边
绕其斜边 旋转一周(假设
旋转一周(假设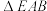 可以穿过正四面体内部),则在旋转过程中,下列结论正确的是( )
可以穿过正四面体内部),则在旋转过程中,下列结论正确的是( )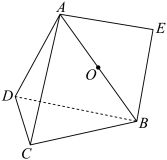
A.三角形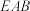 绕斜边 绕斜边 旋转一周形成的旋转体体积为 旋转一周形成的旋转体体积为 |
B.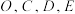 四点共面 四点共面 |
C.点 到 到 的最近距离为 的最近距离为 |
D.异面直线 与 与 所成角的范围为 所成角的范围为 |
您最近一年使用:0次
名校
3 . 设 为正整数,集合
为正整数,集合 对于
对于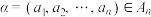 ,设集合
,设集合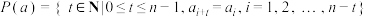 .
.
(1)若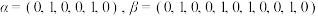 ,写出集合
,写出集合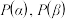 ;
;
(2)若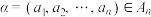 ,且
,且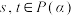 满足
满足 令
令  ,求证:
,求证: 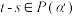 ;
;
(3)若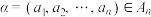 ,且
,且 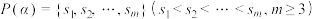 ,求证:
,求证: 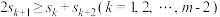 .
.
 为正整数,集合
为正整数,集合 对于
对于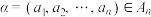 ,设集合
,设集合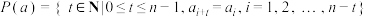 .
.(1)若
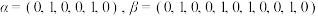 ,写出集合
,写出集合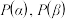 ;
;(2)若
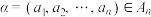 ,且
,且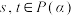 满足
满足 令
令  ,求证:
,求证: 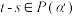 ;
;(3)若
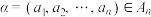 ,且
,且 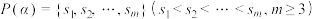 ,求证:
,求证: 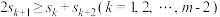 .
.
您最近一年使用:0次
2024-05-09更新
|
1160次组卷
|
4卷引用:安徽省黄山市屯溪第一中学2024-2025学年高一上学期10月数学试卷
安徽省黄山市屯溪第一中学2024-2025学年高一上学期10月数学试卷北京市朝阳区2024届高三下学期质量检测二数学试题(已下线)专题1 以集合为主体的新定义压轴大题【讲】北京市北京师范大学第二附属中学2025届高三上学期期中考试数学试题
名校
解题方法
4 . 黄山是中国著名的旅游胜地,有许多值得打卡的旅游景点,其中包括黄山风景区,齐云山,宏村,徽州古城等. 甲,乙,丙
甲,乙,丙 人准备前往黄山风景区,齐云山,宏村,徽州古城这
人准备前往黄山风景区,齐云山,宏村,徽州古城这 个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩.若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )
个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩.若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )
 甲,乙,丙
甲,乙,丙 人准备前往黄山风景区,齐云山,宏村,徽州古城这
人准备前往黄山风景区,齐云山,宏村,徽州古城这 个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩.若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )
个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩.若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )A. 种 种 | B.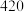 种 种 | C. 种 种 | D. 种 种 |
您最近一年使用:0次
2024-04-13更新
|
1011次组卷
|
3卷引用:安徽省黄山市2024届高中毕业班第二次质量检测数学试题
名校
解题方法
5 . 如图所示.已知椭圆方程为 ,F1、F2为左右焦点,下列命题正确的是( )
,F1、F2为左右焦点,下列命题正确的是( )
 ,F1、F2为左右焦点,下列命题正确的是( )
,F1、F2为左右焦点,下列命题正确的是( )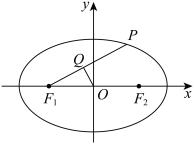
A.P为椭圆上一点,线段PF1中点为Q,则 为定值 为定值 |
B.直线 与椭圆交于R ,S两点,A是椭圆上异与R ,S的点,且 与椭圆交于R ,S两点,A是椭圆上异与R ,S的点,且 、 、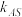 均存在,则 均存在,则 |
C.若椭圆上存在一点M使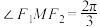 ,则椭圆离心率的取值范围是 ,则椭圆离心率的取值范围是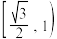 |
D.四边形 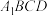 为椭圆内接矩形,则其面积最大值为2ab 为椭圆内接矩形,则其面积最大值为2ab |
您最近一年使用:0次
2023-12-02更新
|
458次组卷
|
4卷引用:安徽省黄山市八校联盟2023-2024学年高二上学期期中考试数学试题
名校
6 . 已知 为圆锥
为圆锥 底面圆
底面圆 的直径,
的直径, ,
,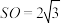 ,点
,点 为圆
为圆 上异于
上异于 的一点,
的一点, 为线段
为线段 上的动点(异于端点),则( )
上的动点(异于端点),则( )
 为圆锥
为圆锥 底面圆
底面圆 的直径,
的直径, ,
,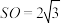 ,点
,点 为圆
为圆 上异于
上异于 的一点,
的一点, 为线段
为线段 上的动点(异于端点),则( )
上的动点(异于端点),则( )A.直线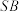 与平面 与平面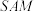 所成角的最大值为 所成角的最大值为 |
B.圆锥 内切球的体积为 内切球的体积为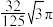 |
C.棱长为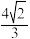 的正四面体可以放在圆锥 的正四面体可以放在圆锥 内 内 |
D.当 为 为 的中点时,满足 的中点时,满足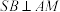 的点 的点 有2个 有2个 |
您最近一年使用:0次
2023-12-02更新
|
753次组卷
|
4卷引用:安徽省黄山市八校联盟2023-2024学年高二上学期期中考试数学试题
7 . 某高中学校在5月20日召开高三毕业典礼,为给高三学生创造轻松的氛围,典礼上有一个“开盲盒”游戏环节,主持人拿出10个盲盒,每个盲盒中装有一个学校标志建筑物的模型,其中有3个“校园”模型,4个“图书馆”模型,2个“名人馆”模型,1个“科技馆”模型.
(1)一次取出2个盲盒,求2个盲盒为同一种模型的概率;
(2)依次不放回地从中取出2个盲盒,求第2次取到的是“图书馆”模型的概率;
(3)甲同学是个“科技狂热粉”,特别想取到“科技馆”模型,主持人为了满足甲同学的愿望,设计如下游戏规则:在一个不透明的袋子中装有大小完全相同的10个小球,其中9个白球,1个红球,有放回的每次摸球一个,摸到红球就可以取走“科技馆”模型,游戏结束.现在让甲同学参与游戏,规定甲同学可以按游戏规则最多摸球10次,若第10次还是摸到白球,主持人直接赠予甲同学“科技馆”模型.设他经过第X次(X=1,2,…,10)摸球并获得“科技馆”模型,求X的分布列.
(1)一次取出2个盲盒,求2个盲盒为同一种模型的概率;
(2)依次不放回地从中取出2个盲盒,求第2次取到的是“图书馆”模型的概率;
(3)甲同学是个“科技狂热粉”,特别想取到“科技馆”模型,主持人为了满足甲同学的愿望,设计如下游戏规则:在一个不透明的袋子中装有大小完全相同的10个小球,其中9个白球,1个红球,有放回的每次摸球一个,摸到红球就可以取走“科技馆”模型,游戏结束.现在让甲同学参与游戏,规定甲同学可以按游戏规则最多摸球10次,若第10次还是摸到白球,主持人直接赠予甲同学“科技馆”模型.设他经过第X次(X=1,2,…,10)摸球并获得“科技馆”模型,求X的分布列.
您最近一年使用:0次
8 . 如图,在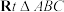 中,
中, ,
,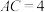 cm,
cm, cm,D是BC边上一点,
cm,D是BC边上一点,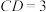 cm,点P为边AC上一动点(点P与A、C不重合),过点P作
cm,点P为边AC上一动点(点P与A、C不重合),过点P作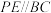 ,交AD于点E.点P以1cm/s的速度从A到C匀速运动.
,交AD于点E.点P以1cm/s的速度从A到C匀速运动. 的取值范围;
的取值范围;
(2)当t为何值时,以PE为半径的⊙E与以DB为半径的⊙D外切?并求此时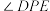 的正切值.
的正切值.
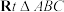 中,
中, ,
,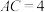 cm,
cm, cm,D是BC边上一点,
cm,D是BC边上一点,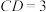 cm,点P为边AC上一动点(点P与A、C不重合),过点P作
cm,点P为边AC上一动点(点P与A、C不重合),过点P作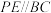 ,交AD于点E.点P以1cm/s的速度从A到C匀速运动.
,交AD于点E.点P以1cm/s的速度从A到C匀速运动.
 的取值范围;
的取值范围;(2)当t为何值时,以PE为半径的⊙E与以DB为半径的⊙D外切?并求此时
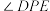 的正切值.
的正切值.
您最近一年使用:0次
2023-06-13更新
|
149次组卷
|
3卷引用:安徽省黄山市屯溪第一中学2022-2023学年高一上学期入学实验班选拔考试模拟试卷(一)
名校
9 . 现有一种不断分裂的细胞 ,每个时间周期
,每个时间周期 内分裂一次,一个
内分裂一次,一个 细胞每次分裂能生成一个或两个新的
细胞每次分裂能生成一个或两个新的 细胞,每次分裂后原
细胞,每次分裂后原 细胞消失,设每次分裂成一个新
细胞消失,设每次分裂成一个新 细胞的概率为
细胞的概率为 ,分裂成两个新
,分裂成两个新 细胞的概率为
细胞的概率为 ;新细胞在下一个周期
;新细胞在下一个周期 内可以继续分裂,每个细胞间相互独立.设有一个初始的
内可以继续分裂,每个细胞间相互独立.设有一个初始的 细胞,在第一个周期
细胞,在第一个周期 中开始分裂,其中
中开始分裂,其中 .
.
(1)设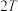 结束后,
结束后, 细胞的数量为
细胞的数量为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)设 结束后,
结束后, 细胞数量为
细胞数量为 的概率为
的概率为 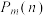 .
.
(i)求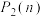 ;
;
(ii)证明: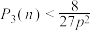 .
.
 ,每个时间周期
,每个时间周期 内分裂一次,一个
内分裂一次,一个 细胞每次分裂能生成一个或两个新的
细胞每次分裂能生成一个或两个新的 细胞,每次分裂后原
细胞,每次分裂后原 细胞消失,设每次分裂成一个新
细胞消失,设每次分裂成一个新 细胞的概率为
细胞的概率为 ,分裂成两个新
,分裂成两个新 细胞的概率为
细胞的概率为 ;新细胞在下一个周期
;新细胞在下一个周期 内可以继续分裂,每个细胞间相互独立.设有一个初始的
内可以继续分裂,每个细胞间相互独立.设有一个初始的 细胞,在第一个周期
细胞,在第一个周期 中开始分裂,其中
中开始分裂,其中 .
.(1)设
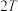 结束后,
结束后, 细胞的数量为
细胞的数量为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)设
 结束后,
结束后, 细胞数量为
细胞数量为 的概率为
的概率为 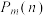 .
.(i)求
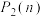 ;
;(ii)证明:
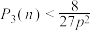 .
.
您最近一年使用:0次
2023-06-03更新
|
2603次组卷
|
6卷引用:安徽省黄山市屯溪第一中学2024届高三第二次模拟考试数学试题(实验班用)
安徽省黄山市屯溪第一中学2024届高三第二次模拟考试数学试题(实验班用)山东省泰安肥城市2023届高考适应性训练数学试题(一)(已下线)模块三 专题7 随机变量及其分布列--拔高能力练(人教A版)(已下线)模块三 专题5 概率--大题分类练--拔高能力练(北师大2019版 高二)湖南省长沙市长郡中学2024届高三上学期月考数学试题(五)安徽省2024届新高考数学预测模拟卷(六)
10 . 点 是直线
是直线 上的一个动点,
上的一个动点, ,
, 是圆
是圆 上的两点.则( )
上的两点.则( )
 是直线
是直线 上的一个动点,
上的一个动点, ,
, 是圆
是圆 上的两点.则( )
上的两点.则( )A.存在 , , , , ,使得 ,使得 |
B.若 , , 均与圆 均与圆 相切,则弦长 相切,则弦长 的最小值为 的最小值为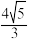 |
C.若 , , 均与圆 均与圆 相切,则直线 相切,则直线 经过一个定点 经过一个定点 |
D.若存在 , , ,使得 ,使得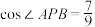 ,则 ,则 点的横坐标的取值范围是 点的横坐标的取值范围是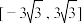 |
您最近一年使用:0次
2023-05-24更新
|
1596次组卷
|
7卷引用:安徽省黄山市屯溪第一中学2024届高三第二次模拟考试数学试题(实验班用)



