名校
1 . 在概率统计中,常常用频率估计概率.已知袋中有若干个红球和白球,有放回地随机摸球 次,红球出现
次,红球出现 次.假设每次摸出红球的概率为
次.假设每次摸出红球的概率为 ,根据频率估计概率的思想,则每次摸出红球的概率
,根据频率估计概率的思想,则每次摸出红球的概率 的估计值为
的估计值为 .
.
(1)若袋中这两种颜色球的个数之比为 ,不知道哪种颜色的球多.有放回地随机摸取3个球,设摸出的球为红球的次数为
,不知道哪种颜色的球多.有放回地随机摸取3个球,设摸出的球为红球的次数为 ,则
,则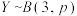 .
.
(注: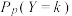 表示当每次摸出红球的概率为
表示当每次摸出红球的概率为 时,摸出红球次数为
时,摸出红球次数为 的概率)
的概率)
(ⅰ)完成下表,并写出计算过程;
(ⅱ)在统计理论中,把使得 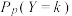 的
的取值达到最大时的  ,作为
,作为 的估计值,记为
的估计值,记为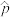 ,请写出
,请写出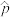 的值.
的值.
(2)把(1)中“使得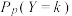 的取值达到最大时的
的取值达到最大时的 作为
作为 的估计值
的估计值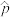 ”的思想称为最大似然原理.基于最大似然原理的最大似然参数估计方法称为最大似然估计.具体步骤:先对参数
”的思想称为最大似然原理.基于最大似然原理的最大似然参数估计方法称为最大似然估计.具体步骤:先对参数 构建对数似然函数
构建对数似然函数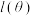 ,再对其关于参数
,再对其关于参数 求导,得到似然方程
求导,得到似然方程 ,最后求解参数
,最后求解参数 的估计值.已知
的估计值.已知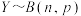 的参数
的参数 的对数似然函数为
的对数似然函数为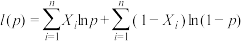 ,其中
,其中 .求参数
.求参数 的估计值,并且说明频率估计概率的合理性.
的估计值,并且说明频率估计概率的合理性.
 次,红球出现
次,红球出现 次.假设每次摸出红球的概率为
次.假设每次摸出红球的概率为 ,根据频率估计概率的思想,则每次摸出红球的概率
,根据频率估计概率的思想,则每次摸出红球的概率 的估计值为
的估计值为 .
.(1)若袋中这两种颜色球的个数之比为
 ,不知道哪种颜色的球多.有放回地随机摸取3个球,设摸出的球为红球的次数为
,不知道哪种颜色的球多.有放回地随机摸取3个球,设摸出的球为红球的次数为 ,则
,则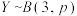 .
.(注:
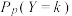 表示当每次摸出红球的概率为
表示当每次摸出红球的概率为 时,摸出红球次数为
时,摸出红球次数为 的概率)
的概率)(ⅰ)完成下表,并写出计算过程;
| 0 | 1 | 2 | 3 |
|
|
| ||
|
|
|
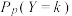 的
的 ,作为
,作为 的估计值,记为
的估计值,记为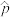 ,请写出
,请写出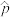 的值.
的值.(2)把(1)中“使得
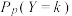 的取值达到最大时的
的取值达到最大时的 作为
作为 的估计值
的估计值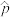 ”的思想称为最大似然原理.基于最大似然原理的最大似然参数估计方法称为最大似然估计.具体步骤:先对参数
”的思想称为最大似然原理.基于最大似然原理的最大似然参数估计方法称为最大似然估计.具体步骤:先对参数 构建对数似然函数
构建对数似然函数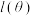 ,再对其关于参数
,再对其关于参数 求导,得到似然方程
求导,得到似然方程 ,最后求解参数
,最后求解参数 的估计值.已知
的估计值.已知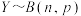 的参数
的参数 的对数似然函数为
的对数似然函数为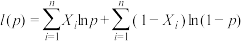 ,其中
,其中 .求参数
.求参数 的估计值,并且说明频率估计概率的合理性.
的估计值,并且说明频率估计概率的合理性.
您最近一年使用:0次
7日内更新
|
202次组卷
|
7卷引用:吉林省长春市实验中学2024届高三下学期对位演练考试数学试卷(一)
吉林省长春市实验中学2024届高三下学期对位演练考试数学试卷(一)浙江省杭州市2024届高三下学期4月教学质量检测数学试题(已下线)压轴题08计数原理、二项式定理、概率统计压轴题6题型汇总重庆市七校联盟2024届高三下学期三诊考试数学试题山东省青岛第一中学2023-2024学年高二下学期第一次模块考试数学试题贵州省贵阳市第一中学等校2024届高三下学期三模数学试题(已下线)专题02 高二下期末真题精选(压轴题 )-高二期末考点大串讲(人教A版2019)
名校
解题方法
2 . 已知全集 ,
,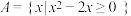 ,
,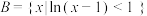 ,则
,则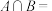 ( )
( )
 ,
,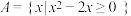 ,
,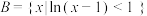 ,则
,则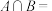 ( )
( )A.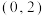 | B. | C. | D. |
您最近一年使用:0次
3 . 已知函数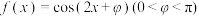 的图象关于点
的图象关于点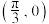 成中心对称,则( )
成中心对称,则( )
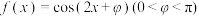 的图象关于点
的图象关于点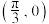 成中心对称,则( )
成中心对称,则( )A. 在区间 在区间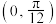 上单调递减 上单调递减 |
B. 在区间 在区间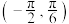 上有两个极值点 上有两个极值点 |
C.直线 是曲线 是曲线 的对称轴 的对称轴 |
D.直线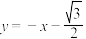 是曲线 是曲线 的切线 的切线 |
您最近一年使用:0次
2024-06-10更新
|
275次组卷
|
2卷引用:吉林省长春市实验中学2023-2024学年高三下学期对位演练考试数学试卷(七)
名校
解题方法
4 . 十七世纪法国数学家费马提出了一个著名的几何问题:“已知一个三角形.求作一点.使其与这个三角形的三个顶点的距离之和最小”.它的答案是:当三角形的三个角均小于 时,则该点与三角形的三个顶点的连线两两成角
时,则该点与三角形的三个顶点的连线两两成角 ;当三角形有一内角大于或等于
;当三角形有一内角大于或等于 时,所求点为三角形最大内角的顶点,在费马问题中,所求点称为费马点.已知在
时,所求点为三角形最大内角的顶点,在费马问题中,所求点称为费马点.已知在 中,
中, ,
,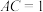 ,
, ,CM是
,CM是 的角平分线,交AB于M,P为
的角平分线,交AB于M,P为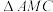 的费马点,则下列说法正确的是( )
的费马点,则下列说法正确的是( )
 时,则该点与三角形的三个顶点的连线两两成角
时,则该点与三角形的三个顶点的连线两两成角 ;当三角形有一内角大于或等于
;当三角形有一内角大于或等于 时,所求点为三角形最大内角的顶点,在费马问题中,所求点称为费马点.已知在
时,所求点为三角形最大内角的顶点,在费马问题中,所求点称为费马点.已知在 中,
中, ,
,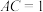 ,
, ,CM是
,CM是 的角平分线,交AB于M,P为
的角平分线,交AB于M,P为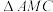 的费马点,则下列说法正确的是( )
的费马点,则下列说法正确的是( )A.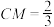 | B.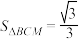 |
C.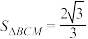 | D.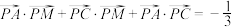 |
您最近一年使用:0次
名校
解题方法
5 . 如图,在 中,
中,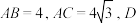 是线段
是线段 上一点(不包括端点),连接
上一点(不包括端点),连接 .
.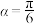 ,求线段
,求线段 的长;
的长;
(2)若 ,求
,求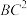 ;
;
(3)设 ,试求
,试求 的取值范围.
的取值范围.
 中,
中,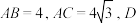 是线段
是线段 上一点(不包括端点),连接
上一点(不包括端点),连接 .
.
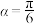 ,求线段
,求线段 的长;
的长;(2)若
 ,求
,求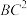 ;
;(3)设
 ,试求
,试求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
6 . 已知 中,内角
中,内角 所对的边分别为
所对的边分别为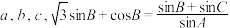 .
.
(1)求角 的值;
的值;
(2)若点 满足
满足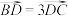 ,且
,且 ,求
,求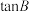 的值.
的值.
 中,内角
中,内角 所对的边分别为
所对的边分别为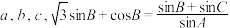 .
.(1)求角
 的值;
的值;(2)若点
 满足
满足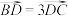 ,且
,且 ,求
,求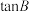 的值.
的值.
您最近一年使用:0次
2024-01-11更新
|
1326次组卷
|
2卷引用:吉林省长春市朝阳区吉大附中实验学校2024届高三下学期开学考试数学试题
名校
7 . (1)计算: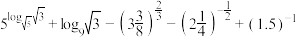 ;
;
(2)已知全集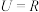 ,集合
,集合 ,
,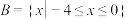 ,求
,求 .
.
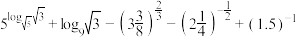 ;
;(2)已知全集
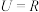 ,集合
,集合 ,
,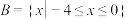 ,求
,求 .
.
您最近一年使用:0次
名校
解题方法
8 . 已知函数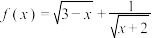 的定义域为集合
的定义域为集合 ,集合
,集合 .
.
(1)当 时,求
时,求 ;
;
(2)若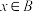 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围.
的取值范围.
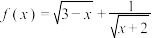 的定义域为集合
的定义域为集合 ,集合
,集合 .
.(1)当
 时,求
时,求 ;
;(2)若
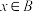 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-10-28更新
|
420次组卷
|
2卷引用:吉林省长春市东北师范大学附属中学2023-2024学年高一上学期10月期中数学试题
9 . 已知函数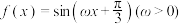 在
在 上有且仅有3个零点,则下列说法不正确的是( )
上有且仅有3个零点,则下列说法不正确的是( )
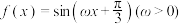 在
在 上有且仅有3个零点,则下列说法不正确的是( )
上有且仅有3个零点,则下列说法不正确的是( )A. 在区间 在区间 上至多有3个极值点 上至多有3个极值点 |
B. 的取值范围是 的取值范围是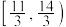 |
C. 在区间 在区间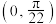 上单调递增 上单调递增 |
D. 的最小正周期可能为 的最小正周期可能为 |
您最近一年使用:0次
名校
解题方法
10 . 已知向量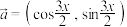 ,
,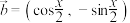 ,
, .
.
(1)求证: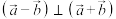 ;
;
(2)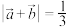 ,求
,求 的值.
的值.
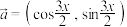 ,
,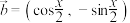 ,
, .
.(1)求证:
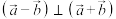 ;
;(2)
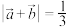 ,求
,求 的值.
的值.
您最近一年使用:0次








