解题方法
1 . 函数 、
、 的定义域均为
的定义域均为 ,若对任意两个不同的实数
,若对任意两个不同的实数 ,
, ,均有
,均有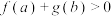 或
或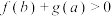 成立,则称
成立,则称 与
与 为相关函数对.
为相关函数对.
(1)判断函数 与
与 是否为相关函数对,并说明理由;
是否为相关函数对,并说明理由;
(2)已知 与
与 为相关函数对,求实数
为相关函数对,求实数 的取值范围;
的取值范围;
(3)已知函数 与
与 为相关函数对,且存在正实数
为相关函数对,且存在正实数 ,对任意实数
,对任意实数 ,均有
,均有 .求证:存在实数
.求证:存在实数 ,使得对任意
,使得对任意 ,均有
,均有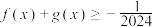 .
.
 、
、 的定义域均为
的定义域均为 ,若对任意两个不同的实数
,若对任意两个不同的实数 ,
, ,均有
,均有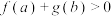 或
或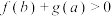 成立,则称
成立,则称 与
与 为相关函数对.
为相关函数对.(1)判断函数
 与
与 是否为相关函数对,并说明理由;
是否为相关函数对,并说明理由;(2)已知
 与
与 为相关函数对,求实数
为相关函数对,求实数 的取值范围;
的取值范围;(3)已知函数
 与
与 为相关函数对,且存在正实数
为相关函数对,且存在正实数 ,对任意实数
,对任意实数 ,均有
,均有 .求证:存在实数
.求证:存在实数 ,使得对任意
,使得对任意 ,均有
,均有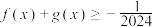 .
.
您最近一年使用:0次
7日内更新
|
416次组卷
|
3卷引用:上海市杨浦区2024届高三下学期二模质量调研数学试卷
2 . 已知定义域为 的函数
的函数 ,其图象是连续的曲线,且存在定义域也为
,其图象是连续的曲线,且存在定义域也为 的导函数
的导函数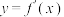 .
.
(1)求函数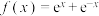 在点
在点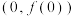 的切线方程;
的切线方程;
(2)已知 ,当
,当 与
与 满足什么条件时,存在非零实数
满足什么条件时,存在非零实数 ,对任意的实数
,对任意的实数 使得
使得 恒成立?
恒成立?
(3)若函数 是奇函数,且满足
是奇函数,且满足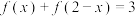 .试判断
.试判断 对任意的实数
对任意的实数 是否恒成立,请说明理由.
是否恒成立,请说明理由.
 的函数
的函数 ,其图象是连续的曲线,且存在定义域也为
,其图象是连续的曲线,且存在定义域也为 的导函数
的导函数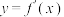 .
.(1)求函数
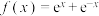 在点
在点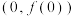 的切线方程;
的切线方程;(2)已知
 ,当
,当 与
与 满足什么条件时,存在非零实数
满足什么条件时,存在非零实数 ,对任意的实数
,对任意的实数 使得
使得 恒成立?
恒成立?(3)若函数
 是奇函数,且满足
是奇函数,且满足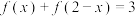 .试判断
.试判断 对任意的实数
对任意的实数 是否恒成立,请说明理由.
是否恒成立,请说明理由.
您最近一年使用:0次
3 . 函数 的表达式为
的表达式为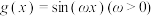 .
.
(1)若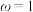 ,直线
,直线 与曲线
与曲线 相切于点
相切于点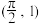 ,求直线
,求直线 的方程;
的方程;
(2)函数 的最小正周期是
的最小正周期是 ,令
,令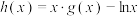 ,将函数
,将函数 的零点由小到大依次记为
的零点由小到大依次记为
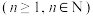 ,证明:数列
,证明:数列 是严格减数列;
是严格减数列;
(3)已知定义在 上的奇函数
上的奇函数 满足
满足 ,对任意
,对任意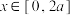 ,当
,当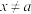 时,都有
时,都有 且
且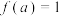 .记
.记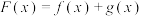 ,
,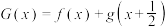 .当
.当 时,是否存在
时,是否存在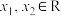 ,使得
,使得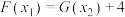 成立?若存在,求出符合题意的
成立?若存在,求出符合题意的 ;若不存在,请说明理由.
;若不存在,请说明理由.
 的表达式为
的表达式为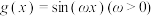 .
.(1)若
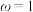 ,直线
,直线 与曲线
与曲线 相切于点
相切于点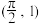 ,求直线
,求直线 的方程;
的方程;(2)函数
 的最小正周期是
的最小正周期是 ,令
,令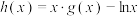 ,将函数
,将函数 的零点由小到大依次记为
的零点由小到大依次记为
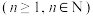 ,证明:数列
,证明:数列 是严格减数列;
是严格减数列;(3)已知定义在
 上的奇函数
上的奇函数 满足
满足 ,对任意
,对任意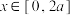 ,当
,当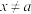 时,都有
时,都有 且
且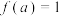 .记
.记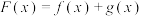 ,
,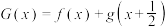 .当
.当 时,是否存在
时,是否存在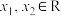 ,使得
,使得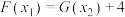 成立?若存在,求出符合题意的
成立?若存在,求出符合题意的 ;若不存在,请说明理由.
;若不存在,请说明理由.
您最近一年使用:0次
解题方法
4 . 已知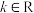 ,记
,记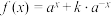 (
( 且
且 ).
).
(1)当 (
( 是自然对数的底)时,试讨论函数
是自然对数的底)时,试讨论函数 的单调性和最值;
的单调性和最值;
(2)试讨论函数 的奇偶性;
的奇偶性;
(3)拓展与探究:
① 当 在什么范围取值时,函数
在什么范围取值时,函数 的图象在
的图象在 轴上存在对称中心?请说明理由;
轴上存在对称中心?请说明理由;
②请提出函数 的一个新性质,并用数学符号语言表达出来.(不必证明)
的一个新性质,并用数学符号语言表达出来.(不必证明)
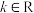 ,记
,记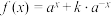 (
( 且
且 ).
).(1)当
 (
( 是自然对数的底)时,试讨论函数
是自然对数的底)时,试讨论函数 的单调性和最值;
的单调性和最值;(2)试讨论函数
 的奇偶性;
的奇偶性;(3)拓展与探究:
① 当
 在什么范围取值时,函数
在什么范围取值时,函数 的图象在
的图象在 轴上存在对称中心?请说明理由;
轴上存在对称中心?请说明理由;②请提出函数
 的一个新性质,并用数学符号语言表达出来.(不必证明)
的一个新性质,并用数学符号语言表达出来.(不必证明)
您最近一年使用:0次
5 . 已知函数 与
与 有相同的定义域
有相同的定义域 .若存在常数
.若存在常数 (
( ),使得对于任意的
),使得对于任意的 ,都存在
,都存在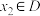 ,满足
,满足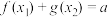 ,则称函数
,则称函数 是函数
是函数 关于
关于 的“
的“ 函数”.
函数”.
(1)若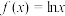 ,
,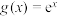 ,试判断函数
,试判断函数 是否是
是否是 关于
关于 的“
的“ 函数”,并说明理由;
函数”,并说明理由;
(2)若函数 与
与 均存在最大值与最小值,且函数
均存在最大值与最小值,且函数 是
是 关于
关于 的“
的“ 函数”,
函数”, 又是
又是 关于
关于 的“
的“ 函数”,证明:
函数”,证明: ;
;
(3)已知 ,
,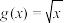 ,其定义域均为
,其定义域均为 .给定正实数
.给定正实数 ,若存在唯一的
,若存在唯一的 ,使得
,使得 是
是 关于
关于 的“
的“ 函数”,求
函数”,求 的所有可能值.
的所有可能值.
 与
与 有相同的定义域
有相同的定义域 .若存在常数
.若存在常数 (
( ),使得对于任意的
),使得对于任意的 ,都存在
,都存在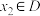 ,满足
,满足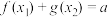 ,则称函数
,则称函数 是函数
是函数 关于
关于 的“
的“ 函数”.
函数”.(1)若
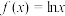 ,
,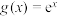 ,试判断函数
,试判断函数 是否是
是否是 关于
关于 的“
的“ 函数”,并说明理由;
函数”,并说明理由;(2)若函数
 与
与 均存在最大值与最小值,且函数
均存在最大值与最小值,且函数 是
是 关于
关于 的“
的“ 函数”,
函数”, 又是
又是 关于
关于 的“
的“ 函数”,证明:
函数”,证明: ;
;(3)已知
 ,
,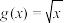 ,其定义域均为
,其定义域均为 .给定正实数
.给定正实数 ,若存在唯一的
,若存在唯一的 ,使得
,使得 是
是 关于
关于 的“
的“ 函数”,求
函数”,求 的所有可能值.
的所有可能值.
您最近一年使用:0次
6 . 对于函数 和
和 ,及区间
,及区间 ,若存在实数
,若存在实数 ,使得
,使得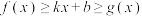 对任意
对任意 恒成立,则称
恒成立,则称 在区间
在区间 上“优于”
上“优于” .有以下两个结论:
.有以下两个结论:
①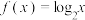 在区间
在区间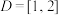 上优于
上优于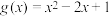 ;
;
②当 时,
时, 在区间
在区间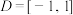 上优于
上优于 .
.
那么( )
 和
和 ,及区间
,及区间 ,若存在实数
,若存在实数 ,使得
,使得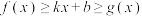 对任意
对任意 恒成立,则称
恒成立,则称 在区间
在区间 上“优于”
上“优于” .有以下两个结论:
.有以下两个结论:①
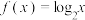 在区间
在区间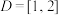 上优于
上优于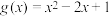 ;
;②当
 时,
时, 在区间
在区间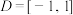 上优于
上优于 .
.那么( )
| A.①、②均正确 | B.①正确,②错误 |
| C.①错误,②正确 | D.①、②均错误 |
您最近一年使用:0次
名校
解题方法
7 . 设函数 的定义域为
的定义域为 ,给定区间
,给定区间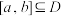 ,若存在
,若存在 ,使得
,使得 ,则称函数
,则称函数 为区间
为区间 上的“均值函数”,
上的“均值函数”, 为函数
为函数 的“均值点”.
的“均值点”.
(1)试判断函数 是否为区间
是否为区间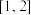 上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;
上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;
(2)已知函数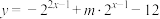 是区间
是区间 上的“均值函数”,求实数
上的“均值函数”,求实数 的取值范围;
的取值范围;
(3)若函数 (常数
(常数 )是区间
)是区间 上的“均值函数”,且
上的“均值函数”,且 为其“均值点”.将区间
为其“均值点”.将区间 任意划分成
任意划分成 (
(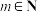 )份,设分点的横坐标从小到大依次为
)份,设分点的横坐标从小到大依次为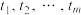 ,记
,记 ,
,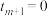 ,
, .再将区间
.再将区间 等分成
等分成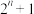 (
( )份,设等分点的横坐标从小到大依次为
)份,设等分点的横坐标从小到大依次为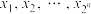 ,记
,记 .求使得
.求使得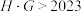 的最小整数
的最小整数 的值.
的值.
 的定义域为
的定义域为 ,给定区间
,给定区间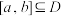 ,若存在
,若存在 ,使得
,使得 ,则称函数
,则称函数 为区间
为区间 上的“均值函数”,
上的“均值函数”, 为函数
为函数 的“均值点”.
的“均值点”.(1)试判断函数
 是否为区间
是否为区间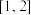 上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;
上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;(2)已知函数
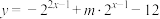 是区间
是区间 上的“均值函数”,求实数
上的“均值函数”,求实数 的取值范围;
的取值范围;(3)若函数
 (常数
(常数 )是区间
)是区间 上的“均值函数”,且
上的“均值函数”,且 为其“均值点”.将区间
为其“均值点”.将区间 任意划分成
任意划分成 (
(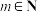 )份,设分点的横坐标从小到大依次为
)份,设分点的横坐标从小到大依次为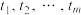 ,记
,记 ,
,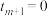 ,
, .再将区间
.再将区间 等分成
等分成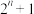 (
( )份,设等分点的横坐标从小到大依次为
)份,设等分点的横坐标从小到大依次为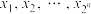 ,记
,记 .求使得
.求使得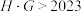 的最小整数
的最小整数 的值.
的值.
您最近一年使用:0次
2023-12-14更新
|
422次组卷
|
4卷引用:上海市金山区2024届高三上学期质量监控数学试题
上海市金山区2024届高三上学期质量监控数学试题(已下线)专题09 导数(三大类型题)15区新题速递(已下线)专题03 函数(三大类型题)15区新题速递广东省广州市第二中学2023-2024学年高二下学期期中考试数学试题
解题方法
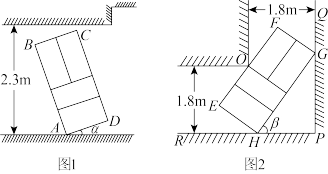
8 . 网络购物行业日益发达,各销售平台通常会配备送货上门服务.小金正在配送客户购买的电冰箱,并获得了客户所在小区门户以及建筑转角处的平面设计示意图. 不能超过
不能超过 ,且底面至少有两个顶点与地面接触.外包装看作长方体,如图1所示,记长方体的纵截面为矩形
,且底面至少有两个顶点与地面接触.外包装看作长方体,如图1所示,记长方体的纵截面为矩形 ,
,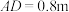 ,
, ,而客户家门高度为
,而客户家门高度为 米,其他过道高度足够.若以倾斜角
米,其他过道高度足够.若以倾斜角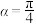 的方式进客户家门,小金能否将冰箱运送入客户家中?计算并说明理由.
的方式进客户家门,小金能否将冰箱运送入客户家中?计算并说明理由.
(2)由于客户选择以旧换新服务,小金需要将客户长方体形状的旧冰箱进行回收.为了省力,小金选择将冰箱水平推运(冰箱背面水平放置于带滚轮的平板车上,平板车长宽均小于冰箱背面).推运过程中遇到一处直角过道,如图2所示,过道宽为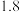 米.记此冰箱水平截面为矩形
米.记此冰箱水平截面为矩形 ,
, .设
.设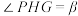 ,当冰箱被卡住时(即点
,当冰箱被卡住时(即点 、
、 分别在射线
分别在射线 、
、 上,点
上,点 在线段
在线段 上),尝试用
上),尝试用 表示冰箱高度
表示冰箱高度 的长,并求出
的长,并求出 的最小值,最后请帮助小金得出结论:按此种方式推运的旧冰箱,其高度的最大值是多少?(结果精确到
的最小值,最后请帮助小金得出结论:按此种方式推运的旧冰箱,其高度的最大值是多少?(结果精确到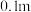 )
)
 不能超过
不能超过 ,且底面至少有两个顶点与地面接触.外包装看作长方体,如图1所示,记长方体的纵截面为矩形
,且底面至少有两个顶点与地面接触.外包装看作长方体,如图1所示,记长方体的纵截面为矩形 ,
,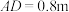 ,
, ,而客户家门高度为
,而客户家门高度为 米,其他过道高度足够.若以倾斜角
米,其他过道高度足够.若以倾斜角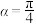 的方式进客户家门,小金能否将冰箱运送入客户家中?计算并说明理由.
的方式进客户家门,小金能否将冰箱运送入客户家中?计算并说明理由.(2)由于客户选择以旧换新服务,小金需要将客户长方体形状的旧冰箱进行回收.为了省力,小金选择将冰箱水平推运(冰箱背面水平放置于带滚轮的平板车上,平板车长宽均小于冰箱背面).推运过程中遇到一处直角过道,如图2所示,过道宽为
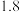 米.记此冰箱水平截面为矩形
米.记此冰箱水平截面为矩形 ,
, .设
.设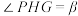 ,当冰箱被卡住时(即点
,当冰箱被卡住时(即点 、
、 分别在射线
分别在射线 、
、 上,点
上,点 在线段
在线段 上),尝试用
上),尝试用 表示冰箱高度
表示冰箱高度 的长,并求出
的长,并求出 的最小值,最后请帮助小金得出结论:按此种方式推运的旧冰箱,其高度的最大值是多少?(结果精确到
的最小值,最后请帮助小金得出结论:按此种方式推运的旧冰箱,其高度的最大值是多少?(结果精确到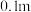 )
)
您最近一年使用:0次
解题方法
9 . 若函数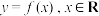 的导函数
的导函数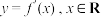 是以
是以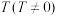 为周期的函数,则称函数
为周期的函数,则称函数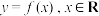 具有“
具有“ 性质”.
性质”.
(1)试判断函数
 和
和 是否具有“
是否具有“ 性质”,并说明理由;
性质”,并说明理由;(2)已知函数
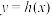 ,其中
,其中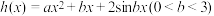 具有“
具有“ 性质”,求函数
性质”,求函数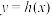 在
在 上的极小值点;
上的极小值点;(3)若函数
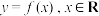 具有“
具有“ 性质”,且存在实数
性质”,且存在实数 使得对任意
使得对任意 都有
都有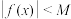 成立,求证:
成立,求证: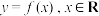 为周期函数.
为周期函数.(可用结论:若函数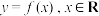 的导函数满足
的导函数满足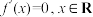 ,则
,则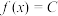 (常数).)
(常数).)
您最近一年使用:0次
解题方法
10 . 函数 满足:对于任意
满足:对于任意 都有
都有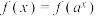 ,(常数
,(常数 ,
, ).给出以下两个命题:①无论
).给出以下两个命题:①无论 取何值,函数
取何值,函数 不是
不是 上的严格增函数;②当
上的严格增函数;②当 时,存在无穷多个开区间
时,存在无穷多个开区间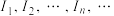 ,使得
,使得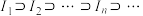 ,且集合
,且集合 对任意正整数
对任意正整数 都成立,则( )
都成立,则( )
| A.①②都正确 | B.①正确②不正确 | C.①不正确②正确 | D.①②都不正确 |
您最近一年使用:0次



