名校
解题方法
1 . 悬链线的原理运用于悬索桥、架空电缆、双曲拱桥、拱坝等工程.通过适当建立坐标系,悬链线可为双曲余弦函数 的图象,类比三角函数的三种性质:①平方关系:①
的图象,类比三角函数的三种性质:①平方关系:①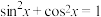 ,②和角公式:
,②和角公式: ,③导数:
,③导数: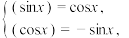 定义双曲正弦函数
定义双曲正弦函数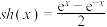 .
.
(1)直接写出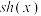 ,
,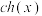 具有的类似①、②、③的三种性质(不需要证明);
具有的类似①、②、③的三种性质(不需要证明);
(2)若当 时,
时, 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)求 的最小值.
的最小值.
 的图象,类比三角函数的三种性质:①平方关系:①
的图象,类比三角函数的三种性质:①平方关系:①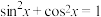 ,②和角公式:
,②和角公式: ,③导数:
,③导数: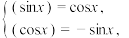 定义双曲正弦函数
定义双曲正弦函数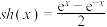 .
.(1)直接写出
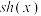 ,
,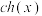 具有的类似①、②、③的三种性质(不需要证明);
具有的类似①、②、③的三种性质(不需要证明);(2)若当
 时,
时, 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(3)求
 的最小值.
的最小值.
您最近一年使用:0次
2024-01-27更新
|
2254次组卷
|
8卷引用:压轴题函数与导数新定义题(九省联考第19题模式)练
(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编(已下线)专题2 函数与导数新定义压轴大题(过关集训)云南省昆明市第一中学2024届高三上学期第六次考前基础强化数学试题2024届高三新改革适应性模拟测试数学试卷一(九省联考题型)浙江省湖州市第一中学2024届高三下学期新高考数学模拟试题江苏省常州高级中学2023-2024学年高二下学期第一次调研考试数学试题2024届山西省平遥县第二中学校高三冲刺调研押题卷数学(二)
名校
2 . 定义:若函数 图象上恰好存在相异的两点
图象上恰好存在相异的两点 满足曲线
满足曲线 在
在 和
和 处的切线重合,则称
处的切线重合,则称 为曲线
为曲线 的“双重切点”,直线
的“双重切点”,直线 为曲线
为曲线 的“双重切线”.
的“双重切线”.
(1)直线 是否为曲线
是否为曲线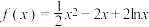 的“双重切线”,请说明理由;
的“双重切线”,请说明理由;
(2)已知函数 求曲线
求曲线 的“双重切线”的方程;
的“双重切线”的方程;
(3)已知函数 ,直线
,直线 为曲线
为曲线 的“双重切线”,记直线
的“双重切线”,记直线 的斜率所有可能的取值为
的斜率所有可能的取值为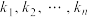 ,若
,若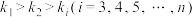 ,证明:
,证明: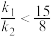 .
.
 图象上恰好存在相异的两点
图象上恰好存在相异的两点 满足曲线
满足曲线 在
在 和
和 处的切线重合,则称
处的切线重合,则称 为曲线
为曲线 的“双重切点”,直线
的“双重切点”,直线 为曲线
为曲线 的“双重切线”.
的“双重切线”.(1)直线
 是否为曲线
是否为曲线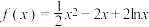 的“双重切线”,请说明理由;
的“双重切线”,请说明理由;(2)已知函数
 求曲线
求曲线 的“双重切线”的方程;
的“双重切线”的方程;(3)已知函数
 ,直线
,直线 为曲线
为曲线 的“双重切线”,记直线
的“双重切线”,记直线 的斜率所有可能的取值为
的斜率所有可能的取值为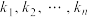 ,若
,若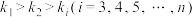 ,证明:
,证明: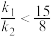 .
.
您最近一年使用:0次
2024-04-17更新
|
1838次组卷
|
9卷引用:专题16 对数平均不等式及其应用【练】
(已下线)专题16 对数平均不等式及其应用【练】(已下线)拔高点突破05 函数与导数背景下的新定义压轴解答题(九大题型)(已下线)周测6 导数与导数的几何意义(提升卷)(已下线)周测6 导数与导数的几何意义 【北京专版】广西2024届高三4月模拟考试数学试卷河北省邢台市2024届高三下学期教学质量检测(一)数学试题(已下线)模块五 专题5 全真拔高模拟5(苏教版高二期中研习)辽宁省辽阳市2023-2024学年高三下学期二模数学试卷陕西省西安市铁一中学2025届高三上学期第三次月考数学试题
名校
解题方法
3 . 已知定义在 的函数
的函数 满足:①对
满足:①对 恒有
恒有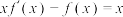 ;②对任意的正数
;②对任意的正数 ,
, 恒有
恒有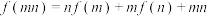 .则下列结论中正确的有( )
.则下列结论中正确的有( )
 的函数
的函数 满足:①对
满足:①对 恒有
恒有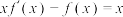 ;②对任意的正数
;②对任意的正数 ,
, 恒有
恒有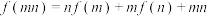 .则下列结论中正确的有( )
.则下列结论中正确的有( )A.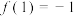 |
B.过点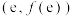 的切线方程 的切线方程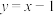 |
C.对 ,不等式 ,不等式 恒成立 恒成立 |
D.若 为函数 为函数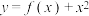 的极值点,则 的极值点,则 |
您最近一年使用:0次
2023-12-08更新
|
1702次组卷
|
7卷引用:第五章 一元函数的导数及其应用(压轴题专练,精选34题)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第二册)
(已下线)第五章 一元函数的导数及其应用(压轴题专练,精选34题)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第二册)湖北省黄冈市部分普通高中2024届高三上学期阶段性教学质量监测数学试题广东省广州市广东实验中学2024届高三上学期大湾区数学冲刺卷(三)江西省抚州市临川第一中学2024届高三“九省联考”考后适应性测试数学试题(一)湖南省长沙市明德中学2023-2024学年高二下学期开学考试数学试卷2024届高三新高考改革数学适应性练习(九省联考题型)广西桂林市国龙外国语学校2024届高三5月适应性考试数学试卷
名校
4 . 根据多元微分求条件极值理论,要求二元函数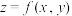 在约束条件
在约束条件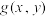 的可能极值点,首先构造出一个拉格朗日辅助函数
的可能极值点,首先构造出一个拉格朗日辅助函数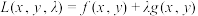 ,其中
,其中 为拉格朗日系数.分别对
为拉格朗日系数.分别对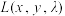 中的
中的 部分求导,并使之为0,得到三个方程组,如下:
部分求导,并使之为0,得到三个方程组,如下:
 ,解此方程组,得出解
,解此方程组,得出解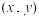 ,就是二元函数
,就是二元函数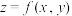 在约束条件
在约束条件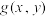 的可能极值点.
的可能极值点. 的值代入到
的值代入到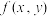 中即为极值.
中即为极值.
补充说明:【例】求函数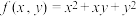 关于变量
关于变量 的导数.即:将变量
的导数.即:将变量 当做常数,即:
当做常数,即: ,下标加上
,下标加上 ,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的
,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的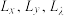 表示分别对
表示分别对 进行求导.
进行求导.
(1)求函数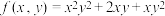 关于变量
关于变量 的导数并求当
的导数并求当 处的导数值.
处的导数值.
(2)利用拉格朗日乘数法求:设实数 满足
满足 ,求
,求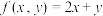 的最大值.
的最大值.
(3)①若 为实数,且
为实数,且 ,证明:
,证明: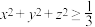 .
.
②设 ,求
,求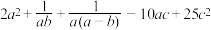 的最小值.
的最小值.
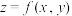 在约束条件
在约束条件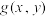 的可能极值点,首先构造出一个拉格朗日辅助函数
的可能极值点,首先构造出一个拉格朗日辅助函数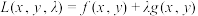 ,其中
,其中 为拉格朗日系数.分别对
为拉格朗日系数.分别对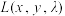 中的
中的 部分求导,并使之为0,得到三个方程组,如下:
部分求导,并使之为0,得到三个方程组,如下: ,解此方程组,得出解
,解此方程组,得出解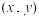 ,就是二元函数
,就是二元函数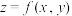 在约束条件
在约束条件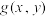 的可能极值点.
的可能极值点. 的值代入到
的值代入到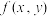 中即为极值.
中即为极值.补充说明:【例】求函数
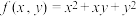 关于变量
关于变量 的导数.即:将变量
的导数.即:将变量 当做常数,即:
当做常数,即: ,下标加上
,下标加上 ,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的
,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的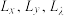 表示分别对
表示分别对 进行求导.
进行求导.(1)求函数
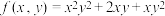 关于变量
关于变量 的导数并求当
的导数并求当 处的导数值.
处的导数值.(2)利用拉格朗日乘数法求:设实数
 满足
满足 ,求
,求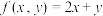 的最大值.
的最大值.(3)①若
 为实数,且
为实数,且 ,证明:
,证明: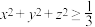 .
.②设
 ,求
,求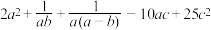 的最小值.
的最小值.
您最近一年使用:0次
名校
5 . 已知 是方程
是方程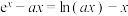 的两个实根,且
的两个实根,且 .
.
(1)求实数 的取值范围;
的取值范围;
(2)已知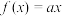 ,
,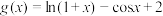 ,若存在正实数
,若存在正实数 ,使得
,使得 成立,证明:
成立,证明: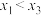 .
.
 是方程
是方程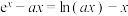 的两个实根,且
的两个实根,且 .
.(1)求实数
 的取值范围;
的取值范围;(2)已知
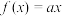 ,
,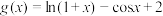 ,若存在正实数
,若存在正实数 ,使得
,使得 成立,证明:
成立,证明: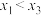 .
.
您最近一年使用:0次
2023-05-26更新
|
1515次组卷
|
6卷引用:第九章 导数与三角函数的联袂 专题三 含三角函数的恒成立问题 微点3 三角函数的恒成立问题(三)
(已下线)第九章 导数与三角函数的联袂 专题三 含三角函数的恒成立问题 微点3 三角函数的恒成立问题(三)(已下线)专题19 导数综合-2浙江省杭州第二中学等四校2023届高三下学期5月高考模拟数学试题 湖南省长沙市第一中学2022-2023学年高二下学期第三次阶段性测试数学试题重庆市万州第二高级中学2024届高三上学期8月月考数学试题2023届浙江省四校联盟高三下学期数学模拟试卷
名校
6 . 已知函数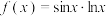 ,则( )
,则( )
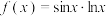 ,则( )
,则( )A.曲线 在 在 处的切线斜率为 处的切线斜率为 |
B.方程 有无数个实数根 有无数个实数根 |
C.曲线 上任意一点与坐标原点连线的斜率均小于 上任意一点与坐标原点连线的斜率均小于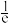 |
D. 在 在 上单调递减 上单调递减 |
您最近一年使用:0次
2024-05-17更新
|
1241次组卷
|
4卷引用:3.4 导数的综合运用
(已下线)3.4 导数的综合运用山东省济南市2024届高三下学期高考针对性训练(5月模拟)数学试题2024届江苏省前黄高级中学高三下学期攀登行动(三)数学试题(已下线)湖北省十堰市郧阳区2024届高三下学期5月月考数学试题
名校
解题方法
7 . 丹麦数学家琴生是19世纪对数学分析做出卓越贡献的巨人,特别是在函数的凸凹性与不等式方向留下了很多宝贵的成果.设函数 在
在 上的导函数为
上的导函数为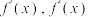 在
在 上的导函数记为
上的导函数记为 ,若在
,若在 上
上 恒成立,则称函数
恒成立,则称函数 在
在 上为“凸函数”,已知
上为“凸函数”,已知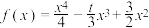 在
在 上为“凸函数”,则实数
上为“凸函数”,则实数 的取值范围是( )
的取值范围是( )
 在
在 上的导函数为
上的导函数为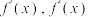 在
在 上的导函数记为
上的导函数记为 ,若在
,若在 上
上 恒成立,则称函数
恒成立,则称函数 在
在 上为“凸函数”,已知
上为“凸函数”,已知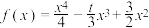 在
在 上为“凸函数”,则实数
上为“凸函数”,则实数 的取值范围是( )
的取值范围是( )A. | B.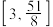 | C.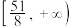 | D.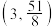 |
您最近一年使用:0次
2023-11-01更新
|
1161次组卷
|
16卷引用:第十章 导数与数学文化 微点2 导数与数学文化(二)
(已下线)第十章 导数与数学文化 微点2 导数与数学文化(二)(已下线)第5.3.2讲 利用导数求解函数的综合问题(第3课时)-2023-2024学年高二数学同步精讲精练宝典(人教A版2019选修第二、三册)(已下线)专题4 导数在不等式中的应用(A)江苏省镇江市句容高级中学2023-2024学年高二上学期10月强基班学情调查数学试题(已下线)专题04 函数的极值与最大(小)值 (十二大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)第10讲 第五章 一元函数的导数及其应用 章节验收测评卷(综合卷)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第二册)江苏省苏州青云实验中学2023-2024学年高二下学期3月月考数学试题(已下线)模块四 专题1 高考新题型专练(新定义专练)(人教A)(高二)宁夏银川市贺兰县第一中学2023-2024学年高二下学期第一阶段考试数学试卷(已下线)模块一 专题4 《导数在不等式中的应用》A基础卷(苏教版)(已下线)模块三 专题3 高考新题型专练 专题2 新定义专练(苏教版)(已下线)模块一 专题4 导数在不等式中的应用A基础卷(高二人教B版)(已下线)模块三 专题2 新定义专练【高二下人教B版】广东省佛山市高明区第一中学2023-2024学年高二下学期第一次大考数学试题四川省遂宁中学校2023-2024学年高二下学期第一次月考(3月)数学试题天津市实验中学滨海学校2023-2024学年高二下学期第一次质量调查数学试题
名校
解题方法
8 . 定义函数 的曲率函数
的曲率函数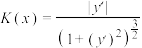 (
(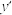 是
是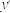 的导函数),函数
的导函数),函数 在
在 处的曲率半径为该点处曲率
处的曲率半径为该点处曲率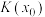 的倒数,曲率半径是函数图象在该点处曲率圆的半径,则下列说法正确的是( )
的倒数,曲率半径是函数图象在该点处曲率圆的半径,则下列说法正确的是( )
 的曲率函数
的曲率函数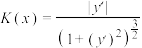 (
(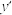 是
是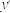 的导函数),函数
的导函数),函数 在
在 处的曲率半径为该点处曲率
处的曲率半径为该点处曲率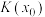 的倒数,曲率半径是函数图象在该点处曲率圆的半径,则下列说法正确的是( )
的倒数,曲率半径是函数图象在该点处曲率圆的半径,则下列说法正确的是( )| A.若曲线在各点处的曲率均不为0,则曲率越大,曲率圆越小 |
B.函数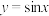 在 在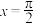 处的曲率半径为1 处的曲率半径为1 |
C.若圆 为函数 为函数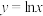 的一个曲率圆,则圆 的一个曲率圆,则圆 半径的最小值为2 半径的最小值为2 |
D.若曲线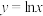 在 在 处的弯曲程度相同,则 处的弯曲程度相同,则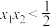 |
您最近一年使用:0次
2024-03-29更新
|
1035次组卷
|
7卷引用:压轴题03不等式压轴题13题型汇总-2
9 . 记函数 的导函数为
的导函数为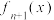 ,已知
,已知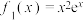 ,若数列
,若数列 ,
, 满足
满足 ,则( )
,则( )
 的导函数为
的导函数为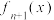 ,已知
,已知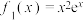 ,若数列
,若数列 ,
, 满足
满足 ,则( )
,则( )A. 为等差数列 为等差数列 | B. 为等比数列 为等比数列 |
C. | D.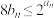 |
您最近一年使用:0次
2024-04-13更新
|
988次组卷
|
6卷引用:第16题 抽象函数与数列结合(一题多变)
(已下线)第16题 抽象函数与数列结合(一题多变)(已下线)压轴题05数列压轴题15题型汇总-32024年普通高等学校招生圆梦杯统一模拟考试(四)数学试题及答案安徽省六安第一中学2024届高三下学期质量检测(三 )数学试卷安徽省六安第一中学2024届高三下学期三模数学试题山西省运城市康杰中学2023-2024学年高三第十九次大型考试数学仿真训练试题
解题方法
10 . 贝塞尔曲线(Beziercurve)是应用于二维图形应用程序的数学曲线,一般的矢量图形软件通过它来精确画出曲线.三次函数 的图象是可由
的图象是可由 ,
, ,
, ,
, 四点确定的贝塞尔曲线,其中
四点确定的贝塞尔曲线,其中 ,
, 在
在 的图象上,
的图象上, 在点
在点 ,
, 处的切线分别过点
处的切线分别过点 ,
, .若
.若 ,
,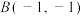 ,
,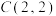 ,
,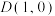 ,则
,则 ( )
( )
 的图象是可由
的图象是可由 ,
, ,
, ,
, 四点确定的贝塞尔曲线,其中
四点确定的贝塞尔曲线,其中 ,
, 在
在 的图象上,
的图象上, 在点
在点 ,
, 处的切线分别过点
处的切线分别过点 ,
, .若
.若 ,
,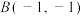 ,
,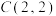 ,
,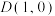 ,则
,则 ( )
( )A.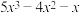 | B. |
C. | D. |
您最近一年使用:0次
2024-05-17更新
|
961次组卷
|
7卷引用:5.2导数的基本运算
(已下线)5.2导数的基本运算(已下线)拔高点突破01 函数的综合应用(九大题型)-2(已下线)重难点突破03 三次函数的图象和性质 (八大题型)-1(已下线)第五章 概率统计创新问题 专题七 概率统计中的新定义问题 微点5 概率统计中的新定义问题综合训练【培优版】江苏省决胜新高考2024届高三下学期4月大联考数学试题江苏省常州市金坛第四中学2024届高三考前适应性考试(三模)数学试题江苏省如东县、宿迁一中、沭阳如东中学2023-2024学年高三下学期期中学情检测数学试题



