名校
解题方法
1 . 如图,在正方体 中,
中, 分别为
分别为 的中点,则直线
的中点,则直线 和
和 夹角的余弦值为( )
夹角的余弦值为( )
 中,
中, 分别为
分别为 的中点,则直线
的中点,则直线 和
和 夹角的余弦值为( )
夹角的余弦值为( )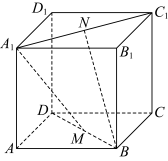
A.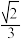 | B. | C. | D. |
您最近一年使用:0次
昨日更新
|
1557次组卷
|
11卷引用:安徽省亳州市第二完全中学2024-2025学年高二上学期第一次月考数学试卷
安徽省亳州市第二完全中学2024-2025学年高二上学期第一次月考数学试卷河南省实验中学2024-2025学年高二上学期第一次月考数学试卷河北省承德双滦圣泉高级中学2024-2025学年高二上学期9月月考数学试卷海南省华中师范大学琼中附属中学2024-2025学年高二上学期第一次月考(10月)数学试题四川省南充高级中学2024-2025学年高三上学期10月检测数学试题四川省南充高级中学2024-2025学年高二上学期10月月考数学试题贵州省铜仁市松桃苗族自治县第三高级中学2024-2025学年高二上学期10月月考数学试题四川省南充市嘉陵第一中学2024-2025学年高二上学期第一次月考数学试题四川省眉山育英实验学校2024-2025学年高二上学期10月月考数学试卷贵州省贵阳市乌当区某校2024-2025学年高二上学期10月月考数学试题湖北省十堰市六校教学合作体2024-2025学年高二上学期10月月考数学试题
名校
2 . 如图,在棱长为1的正方体 中,
中,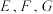 分别是
分别是 ,
,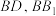 的中点.
的中点. ;
;
(2)求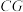 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中,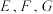 分别是
分别是 ,
, 的中点.
的中点.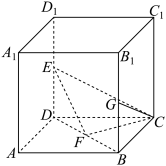
 ;
;(2)求
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
昨日更新
|
539次组卷
|
2卷引用:安徽省合肥市第七中学2025届高三上学期第四次统一作业数学试题
名校
3 . 如图,四棱锥 中,侧面
中,侧面 为等边三角形,O为线段
为等边三角形,O为线段 的中点且
的中点且 底面
底面 ,
,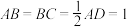 ,
,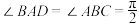 ,E是
,E是 的中点.
的中点.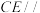 平面
平面 ;
;
(2)点M为棱 的中点,求平面
的中点,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 中,侧面
中,侧面 为等边三角形,O为线段
为等边三角形,O为线段 的中点且
的中点且 底面
底面 ,
,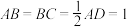 ,
,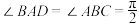 ,E是
,E是 的中点.
的中点.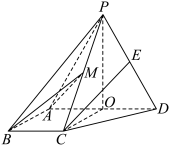
 平面
平面 ;
;(2)点M为棱
 的中点,求平面
的中点,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
名校
解题方法
4 . 已知异面直线 所成的角为
所成的角为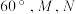 在直线
在直线 上,
上, 在直线
在直线 上,
上, ,
, ,
,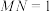 ,
,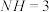 ,
, ,则
,则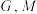 间的距离为
间的距离为_________ .
 所成的角为
所成的角为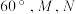 在直线
在直线 上,
上, 在直线
在直线 上,
上,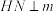 ,
, ,
,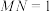 ,
,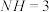 ,
, ,则
,则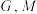 间的距离为
间的距离为
您最近一年使用:0次
名校
解题方法
5 . 如图,在四棱锥 中,
中,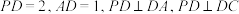 ,底面
,底面 为正方形,
为正方形, 分别为
分别为 的中点.
的中点. ∥平面
∥平面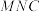 ;
;
(2)求直线 与平面
与平面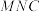 所成角的正弦值;
所成角的正弦值;
(3)求点 到平面
到平面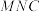 的距离.
的距离.
 中,
中,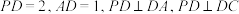 ,底面
,底面 为正方形,
为正方形, 分别为
分别为 的中点.
的中点.
 ∥平面
∥平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)求点
 到平面
到平面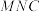 的距离.
的距离.
您最近一年使用:0次
2024-08-31更新
|
4189次组卷
|
9卷引用:安徽省阜阳市红旗中学2024-2025学年高二上学期第一次月考(10月)数学试题
安徽省阜阳市红旗中学2024-2025学年高二上学期第一次月考(10月)数学试题湖南省张家界市慈利县第一中学2024-2025学年高二下学期第一次月考数学试卷内蒙古自治区巴彦淖尔市第一中学2025届高三上学期第三次学业诊断(10月)数学试卷四川省绵竹中学2024-2025学年高二上学期10月月考数学试题四川省南充市嘉陵第一中学2024-2025学年高二上学期第一次月考数学试题天津市第四十三中学2024-2025学年高二上学期阶段性质量检测数学试题北京市北京大学附属中学行知学院2022-2023学年高二上学期期中考试数学试卷山东省北镇中学2024-2025学年高二上学期第一次(开学)考试数学试题(已下线)模块一 基础第1套 模拟卷(高二期中备考模拟)
名校
解题方法
6 . 如图,在棱长为2的正方体 中,点P是正方体的上底面
中,点P是正方体的上底面 内(不含边界)的动点,点Q是棱
内(不含边界)的动点,点Q是棱 的中点,则以下命题正确的是( )
的中点,则以下命题正确的是( )
 中,点P是正方体的上底面
中,点P是正方体的上底面 内(不含边界)的动点,点Q是棱
内(不含边界)的动点,点Q是棱 的中点,则以下命题正确的是( )
的中点,则以下命题正确的是( )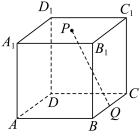
A.三棱锥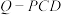 的体积是定值 的体积是定值 |
B.存在点P,使得 与 与 所成的角为 所成的角为 |
C.直线 与平面 与平面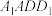 所成角的正弦值的取值范围为 所成角的正弦值的取值范围为 |
D.若 ,则P的轨迹的长度为 ,则P的轨迹的长度为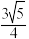 |
您最近一年使用:0次
2024-08-08更新
|
1787次组卷
|
16卷引用:安徽省蚌埠市五河第一中学2024-2025学年高二上学期学科培优数学试题
安徽省蚌埠市五河第一中学2024-2025学年高二上学期学科培优数学试题河北省保定市曲阳县第一高级中学2024-2025学年高二上学期9月月考数学试题山东省济宁市育才中学2024-2025学年高二上学期10月月考数学试题福建省厦门市松柏中学2024-2025学年高二上学期月考1数学试卷陕西省西安市西光中学2024-2025学年高二上学期10月月考数学试题福建省南安市侨光中学2024-2025学年高二上学期第1次阶段考试(10月)数学试题广东省普宁华侨中学2024-2025学年高二上学期第一次月考数学试卷内蒙古赤峰市赤峰二中2024-2025学年高二上学期第一次月考数学试题青海省西宁市海湖中学2024-2025学年高二上学期第一阶段测试数学试题湖南省部分学校A佳联考2023-2024学年高三5月模拟考试数学试题福建省部分学校2025届新高三暑期成果联合质量检测数学试卷(已下线)第七章 立体几何与空间向量(测试)(已下线)拔高点突破02 立体几何中的动态、轨迹问题(六大题型)山西省运城市盐湖区第五高级中学2025届高三上学期开学考试数学试卷山东省东营市利津县高级中学2025届高三上学期开学收心考试数学试题湖南省邵阳市邵阳县第二高级中学2024-2025学年高二上学期入学考试数学试题
名校
解题方法
7 . 图①是直角梯形 ,四边形
,四边形 是边长为2的菱形,并且
是边长为2的菱形,并且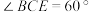 ,以
,以 为折痕将
为折痕将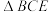 折起,使点
折起,使点 到达
到达 的位置,且
的位置,且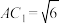 .
.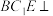 平面
平面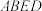 ;
;
(2)在棱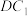 上是否存在点
上是否存在点 ,使得点
,使得点 到平面
到平面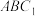 的距离为
的距离为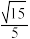 ?若存在,求出直线
?若存在,求出直线 与平面
与平面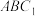 所成角的正弦值:若不存在,请说明理由.
所成角的正弦值:若不存在,请说明理由.
 ,四边形
,四边形 是边长为2的菱形,并且
是边长为2的菱形,并且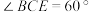 ,以
,以 为折痕将
为折痕将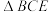 折起,使点
折起,使点 到达
到达 的位置,且
的位置,且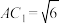 .
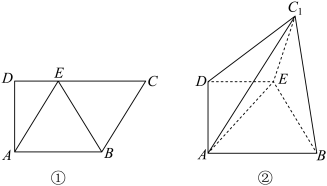
.
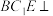 平面
平面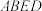 ;
;(2)在棱
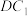 上是否存在点
上是否存在点 ,使得点
,使得点 到平面
到平面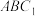 的距离为
的距离为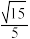 ?若存在,求出直线
?若存在,求出直线 与平面
与平面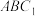 所成角的正弦值:若不存在,请说明理由.
所成角的正弦值:若不存在,请说明理由.
您最近一年使用:0次
2024-07-02更新
|
628次组卷
|
5卷引用:安徽省安庆市太湖中学2023-2024学年高二上学期第一次段考数学试题
名校
8 . 如图,在几何体 中,底面
中,底面 为边长为2的正方形,
为边长为2的正方形, 平面
平面 .
.
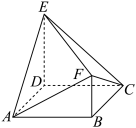
(1)证明: 平面
平面  ;
;
(2)求二面角 的大小.
的大小.
 中,底面
中,底面 为边长为2的正方形,
为边长为2的正方形, 平面
平面 .
.
(1)证明:
 平面
平面  ;
;(2)求二面角
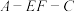 的大小.
的大小.
您最近一年使用:0次
名校
解题方法
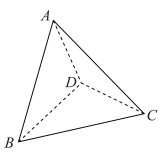
9 . 在荾形 中,
中, ,
, ,将菱形
,将菱形 沿着
沿着 翻折,得到三棱锥
翻折,得到三棱锥 如图所示,此时
如图所示,此时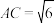 .
.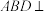 平面
平面 ;
;
(2)若点 是
是 的中点,求直线
的中点,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, ,
, ,将菱形
,将菱形 沿着
沿着 翻折,得到三棱锥
翻折,得到三棱锥 如图所示,此时
如图所示,此时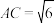 .
.
 平面
平面 ;
;(2)若点
 是
是 的中点,求直线
的中点,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-12-31更新
|
463次组卷
|
5卷引用:安徽省滁州市明光市第三中学2023-2024学年高二上学期11月月考数学
名校
解题方法
10 . 如图,四棱锥 中,底面
中,底面 是矩形,
是矩形, ,
, ,
, ,
, ,
, 是等腰三角形,点
是等腰三角形,点 是棱
是棱 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值是( )
所成角的余弦值是( )
 中,底面
中,底面 是矩形,
是矩形, ,
, ,
, ,
, ,
, 是等腰三角形,点
是等腰三角形,点 是棱
是棱 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值是( )
所成角的余弦值是( )
A. | B. | C.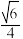 | D. |
您最近一年使用:0次
2023-12-25更新
|
1671次组卷
|
24卷引用:安徽省宿州市泗县第一中学2020-2021学年高二上学期第二次月考数学(理)试题
安徽省宿州市泗县第一中学2020-2021学年高二上学期第二次月考数学(理)试题吉林省延边第二中学2020-2021学年高二上学期第二次考试月考数学(理)试题黑龙江省大庆中学2020-2021学年高三10月月考数学(文)试题江苏省苏南八校2023-2024学年高二创新班上学期12月联考数学试题江苏省苏南八校2023-2024学年高二上学期12月联考数学试卷2020高考命题专家预测密卷理科数学(一)试题2020高考命题专家预测密卷文科数学(一)试题(已下线)第36讲 空间向量的应用-2021年新高考数学一轮专题复习(新高考专版)(已下线)1.4.2 空间向量的应用(二)(精讲)-2020-2021学年一隅三反系列之高二数学新教材选择性必修第一册(人教版A版)(已下线)考点18 空间中的角度和距离问题-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)吉林省长春市十一高中2022-2023学年高三下学期期初考试数学试题人教A版(2019) 选修第一册 数学奇书 第一章 空间向量与立体几何 1.4.2 用空间向量研究距离、夹角问题 第2课时 用空间向量研究夹角问题人教A版(2019) 选修第一册 第一章 阶段测评(一)空间向量与立体几何新疆维吾尔自治区乌鲁木齐市第一中学2023届高三第三次诊断性测试数学(理)试题广东省江门市新会第一中学2023-2024学年高二上学期期中考试数学试题广东省江门市某校2023-2024学年高二上学期期中考试数学试题北京市西城区2023-2024学年高二上学期期末模拟练习数学试题(已下线)专题13 空间向量的应用10种常见考法归类(1)福建省莆田五中、莆田八中、莆田十中、莆田侨中2023-2024学年高二上学期期末联考数学试卷(已下线)高二数学开学摸底考02(江苏专用)-2023-2024学年高中下学期开学摸底考试卷(已下线)6.3 空间向量的应用 (3)(已下线)专题7.3 空间角与空间中的距离问题【九大题型】(已下线)1.4.2用空间向量研究距离、夹角问题——课后作业(基础版)河北省邯郸市三龙育华中学2023-2024学年高一下学期期末考试数学卷



