名校
1 . 已知函数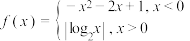 ,若方程
,若方程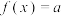 有四个不同的解
有四个不同的解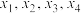 ,且
,且 ,
,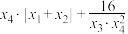 的取值范围是
的取值范围是______ ..
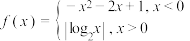 ,若方程
,若方程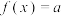 有四个不同的解
有四个不同的解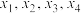 ,且
,且 ,
,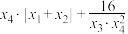 的取值范围是
的取值范围是
您最近一年使用:0次
2024-09-20更新
|
623次组卷
|
3卷引用:安徽省六校2025届高三上学期第一次阶段联合教学质量测评数学试卷
名校
解题方法
2 . 已知 ,
, 是双曲线
是双曲线 的左、右焦点,
的左、右焦点,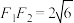 ,点
,点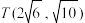 在
在 上.
上.
(1)求 的方程
的方程
(2)设直线 过点
过点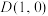 ,且与
,且与 交于
交于 ,
, 两点.
两点.
①若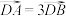 ,求
,求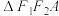 的面积;
的面积;
②以线段 为直径的圆交
为直径的圆交 轴于
轴于 ,
, 两点,若
两点,若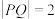 ,求直线
,求直线 的方程.
的方程.
 ,
, 是双曲线
是双曲线 的左、右焦点,
的左、右焦点,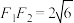 ,点
,点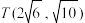 在
在 上.
上.(1)求
 的方程
的方程(2)设直线
 过点
过点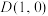 ,且与
,且与 交于
交于 ,
, 两点.
两点.①若
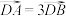 ,求
,求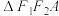 的面积;
的面积;②以线段
 为直径的圆交
为直径的圆交 轴于
轴于 ,
, 两点,若
两点,若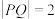 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2024-09-20更新
|
450次组卷
|
2卷引用:安徽省阜阳市第三中学2024-2025学年高二上学期第一次调研考试数学试题(A卷)
名校
解题方法
3 . 已知函数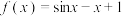 ,若关于x的不等式
,若关于x的不等式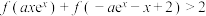 的解集中有且仅有2个正整数,则实数a的取值范围为
的解集中有且仅有2个正整数,则实数a的取值范围为________ .
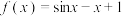 ,若关于x的不等式
,若关于x的不等式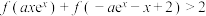 的解集中有且仅有2个正整数,则实数a的取值范围为
的解集中有且仅有2个正整数,则实数a的取值范围为
您最近一年使用:0次
2024-09-18更新
|
842次组卷
|
8卷引用:安徽省芜湖市第二中学2023-2024学年高三上学期第三次测试数学试题
名校
4 . 设 ,
, ,且
,且 ,则下列关系式可能成立的是( )
,则下列关系式可能成立的是( )
 ,
, ,且
,且 ,则下列关系式可能成立的是( )
,则下列关系式可能成立的是( )A. | B.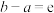 | C.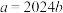 | D. |
您最近一年使用:0次
2024-09-13更新
|
446次组卷
|
5卷引用:安徽省合肥市第七中学2025届高三上学期第四次统一作业数学试题
名校
5 . 设 ,若
,若 时,均有
时,均有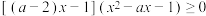 成立,则实数
成立,则实数 的取值
的取值集合 为_____
 ,若
,若 时,均有
时,均有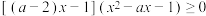 成立,则实数
成立,则实数 的取值
的取值
您最近一年使用:0次
2024-09-09更新
|
1219次组卷
|
9卷引用:安徽省合肥市合肥一六八中学2024-2025学年高一上学期第一次月考数学试题
安徽省合肥市合肥一六八中学2024-2025学年高一上学期第一次月考数学试题上海市华东师范大学第三附属中学2025届高三上学期第一次阶段测试数学试题江西省赣州市瑞金第一中学2024-2025学年高一上学期第一次月考数学试题四川省成都市锦江区嘉祥外国语高级中学2024-2025学年高一上学期10月阶段性学业反馈数学试题广东省广州市铁一中学2024-2025学年高一上学期10月月考数学试题广东省广州市华南师范大学附属中学2024-2025学年高一上学期10月数学教学检测(一)广东省惠州市泰雅实验高中2024-2025学年高一上学期第一次月考数学试题河南省郑州市第四高级中学2024-2025学年高一上学期9月月考数学试卷.上海市延安中学2024-2025学年高一上学期新生综合素质检测数学试卷
名校
6 . 定义在 上的函数
上的函数 和
和 的最小周期分别是
的最小周期分别是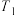 和
和 ,已知
,已知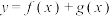 的最小正周期为1,则下列选项中可能成立的是( )
的最小正周期为1,则下列选项中可能成立的是( )
 上的函数
上的函数 和
和 的最小周期分别是
的最小周期分别是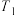 和
和 ,已知
,已知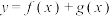 的最小正周期为1,则下列选项中可能成立的是( )
的最小正周期为1,则下列选项中可能成立的是( )A. | B. |
C.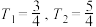 | D. |
您最近一年使用:0次
2024-09-08更新
|
253次组卷
|
2卷引用:安徽省合肥市第七中学2025届高三上学期第四次统一作业数学试题
24-25高三上·安徽·阶段练习
名校
解题方法
7 . 已知 的定义域为
的定义域为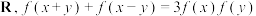 ,且
,且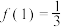 ,则
,则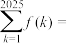 ( )
( )
 的定义域为
的定义域为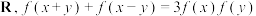 ,且
,且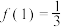 ,则
,则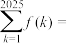 ( )
( )A. | B. | C. | D. |
您最近一年使用:0次
2024-09-06更新
|
2226次组卷
|
8卷引用:安徽省县中联盟2024-2025学年高三上学期9月联考数学试题
(已下线)安徽省县中联盟2024-2025学年高三上学期9月联考数学试题 湖南省长沙市六校2025届高三九月大联考数学试卷湖北省部分州市2025届高三上学期9月月考联合测评数学试题广西柳州高级中学2024-2025学年高三上学期9月自主综合考试数学试题福建省厦门集美中学2025届高三上学期十月月考数学试卷(已下线)2.3函数的奇偶性和周期性【同步课时】北京专版湖南省长沙市六校2025届高三九月大联考数学试卷陕西省西安市高新第一中学2024-2025学年高三上学期第二次模拟考试数学试题
名校
解题方法
8 . 激光的单光子通讯过程可用如下棋型求述:发送方将信息加密后选择某种特定偏振状态的单光子进行发送,在信息传输过程中,若存在窃听者,由于密码本的缺失,窃听者不一定能正确解密并获取准确信息.某次实验中,假设原始信息的单光子的偏振状态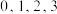 等可能地出现,原始信息的单光子的偏振状态与窃听者的解密信息的单光子的偏振状态有如下对应关系.
等可能地出现,原始信息的单光子的偏振状态与窃听者的解密信息的单光子的偏振状态有如下对应关系.
已知原始信息的任意一种单光子的偏振状态,对应的窃听者解密信息的单光子的偏振状态等可能地出现.
(1)若发送者发送的原始信息的单光子的偏振状态为1,求窃听者解密信息的单光子的偏振状态与原始信息的单光子的偏振状态相同的概率;
(2)若发送者连续三次发送的原始信息的单光子的偏振状态均为1,设窃听者解密信息的单光子的偏振状态为1的个数为X,求X的分布列和数学期望 ;
;
(3)已知发送者连续三次发送值息,窃听者解密信息的单光子的偏振状态均为1.设原始信息的单光子只有一种偏振状态的可能性为a,有两种偏振状态的可能性为b,有三种偏振状态的可能性为c,试比较 的大小关系.
的大小关系.
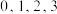 等可能地出现,原始信息的单光子的偏振状态与窃听者的解密信息的单光子的偏振状态有如下对应关系.
等可能地出现,原始信息的单光子的偏振状态与窃听者的解密信息的单光子的偏振状态有如下对应关系.| 原始信息的单光子的偏振状态 | 0 | 1 | 2 | 3 |
| 解密信息的单光子的偏振状态 |
|
|
|
|
(1)若发送者发送的原始信息的单光子的偏振状态为1,求窃听者解密信息的单光子的偏振状态与原始信息的单光子的偏振状态相同的概率;
(2)若发送者连续三次发送的原始信息的单光子的偏振状态均为1,设窃听者解密信息的单光子的偏振状态为1的个数为X,求X的分布列和数学期望
 ;
;(3)已知发送者连续三次发送值息,窃听者解密信息的单光子的偏振状态均为1.设原始信息的单光子只有一种偏振状态的可能性为a,有两种偏振状态的可能性为b,有三种偏振状态的可能性为c,试比较
 的大小关系.
的大小关系.
您最近一年使用:0次
名校
解题方法
9 . 设函数 的定义域为
的定义域为 ,满足
,满足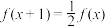 ,且当
,且当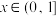 时,
时,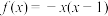 .若对任意
.若对任意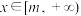 ,都有
,都有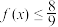 ,则
,则 的取值范围是
的取值范围是___________ .
 的定义域为
的定义域为 ,满足
,满足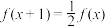 ,且当
,且当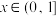 时,
时,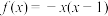 .若对任意
.若对任意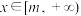 ,都有
,都有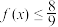 ,则
,则 的取值范围是
的取值范围是
您最近一年使用:0次
2024-08-26更新
|
942次组卷
|
4卷引用:安徽省黄山市屯溪第一中学2024-2025学年高一上学期10月数学试卷
名校
解题方法
10 . 函数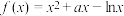 .
.
(1)若函数 在区间
在区间 上单调递增,求a的取值范围;
上单调递增,求a的取值范围;
(2)当 时,讨论函数
时,讨论函数 在区间
在区间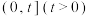 上的单调性.
上的单调性.
(3)当 时,证明:当
时,证明:当 时,
时,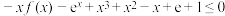 .
.
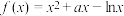 .
.(1)若函数
 在区间
在区间 上单调递增,求a的取值范围;
上单调递增,求a的取值范围;(2)当
 时,讨论函数
时,讨论函数 在区间
在区间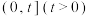 上的单调性.
上的单调性.(3)当
 时,证明:当
时,证明:当 时,
时,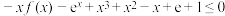 .
.
您最近一年使用:0次