1 . 已知 为等差数列
为等差数列 的前n项和,
的前n项和,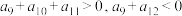 ,则下列选项正确的是( )
,则下列选项正确的是( )
 为等差数列
为等差数列 的前n项和,
的前n项和,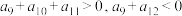 ,则下列选项正确的是( )
,则下列选项正确的是( )A.数列 是单调递增数列 是单调递增数列 | B.当 时, 时, 最大 最大 |
C.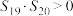 | D.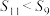 |
您最近一年使用:0次
2 . 已知数列 的前n项和为
的前n项和为 ,
,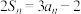 ,其中
,其中 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前n项和
的前n项和 ,若对任意
,若对任意 且
且 ,
,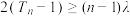 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的前n项和为
的前n项和为 ,
,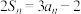 ,其中
,其中 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
 ,数列
,数列 的前n项和
的前n项和 ,若对任意
,若对任意 且
且 ,
,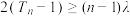 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-02-05更新
|
844次组卷
|
4卷引用:山西省运城市2023-2024学年高二上学期期末调研测试数学试题
解题方法
3 . 已知正项数列 满足
满足 ,数列
,数列 的前
的前 项和为
项和为 ,且
,且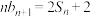 ,
,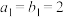 .
.
(1)求 ,
, 的通项公式;
的通项公式;
(2)证明: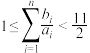 .
.
 满足
满足 ,数列
,数列 的前
的前 项和为
项和为 ,且
,且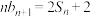 ,
,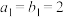 .
.(1)求
 ,
, 的通项公式;
的通项公式;(2)证明:
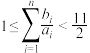 .
.
您最近一年使用:0次
解题方法
4 . 已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求 的通项公式;
的通项公式;
(2)设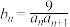 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,且
,且 .
.(1)求
 的通项公式;
的通项公式;(2)设
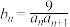 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
2024-01-28更新
|
702次组卷
|
3卷引用:山西省忻州市2023-2024学年高二上学期1月期末考试数学试题
名校
5 . 若数列 满足
满足 ,
, ,则
,则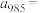 ( )
( )
 满足
满足 ,
, ,则
,则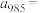 ( )
( )A. | B.11 | C.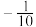 | D.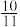 |
您最近一年使用:0次
2024-01-28更新
|
1530次组卷
|
8卷引用:山西省忻州市2023-2024学年高二上学期1月期末考试数学试题
6 . 已知数列的前4项分别为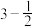 ,
, ,
,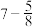 ,
,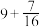 ,则该数列的一个通项公式可以为
,则该数列的一个通项公式可以为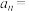 ( )
( )
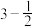 ,
, ,
,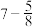 ,
,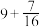 ,则该数列的一个通项公式可以为
,则该数列的一个通项公式可以为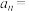 ( )
( )A. |
B.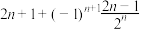 |
C.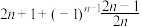 |
D.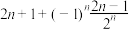 |
您最近一年使用:0次
2024-01-28更新
|
241次组卷
|
3卷引用:山西省忻州市2023-2024学年高二上学期1月期末考试数学试题
名校
解题方法
7 . 已知在等差数列 中,
中,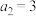 ,
, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足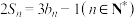 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设
 ,求数列
,求数列 的前
的前 项和
项和 .
.
 中,
中,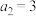 ,
, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足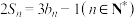 .
.(1)求数列
 和
和 的通项公式;
的通项公式;(2)设

 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
2024-01-26更新
|
1741次组卷
|
4卷引用:山西省太原市2024届高三上学期期末学业诊断数学试题
山西省太原市2024届高三上学期期末学业诊断数学试题浙江省嘉兴市第一中学2024届高三第一次模拟测试数学试题(已下线)第一章 数列(单元综合检测卷) -2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)4.3.2 等比数列的前n项和公式——随堂检测
名校
8 . 在数列 ,
, ,
, ,
, ,
, …中,根据前5项的规律写出的第12个数为( )
…中,根据前5项的规律写出的第12个数为( )
 ,
, ,
, ,
, ,
, …中,根据前5项的规律写出的第12个数为( )
…中,根据前5项的规律写出的第12个数为( )A. | B.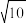 | C. | D. |
您最近一年使用:0次
2024-01-25更新
|
494次组卷
|
5卷引用:山西省长治市2023-2024学年高二上学期1月期末数学试题
山西省长治市2023-2024学年高二上学期1月期末数学试题(已下线)1.1 数列的概念4种常见考法归类-【帮课堂】2023-2024学年高二数学同步学与练(北师大版2019选择性必修第二册)江西省宜春市第三中学2023-2024学年高二下学期第一次月考数学试卷(B卷)江西省上饶市蓝天教育集团2023-2024学年高二下学期期中考试数学试题广东省肇庆市龙涛外国语学校高中部2024届高三第三次高考模拟测试数学试卷
解题方法
9 . 两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画出点或用小石子表示数,按照点或小石子能排列的形状对数进行分类,如下图中实心点的个数依次为5,9,14,20,…,这样的一组数被称为梯形数,记此数列为 ,则( )
,则( )

 ,则( )
,则( )
A.存在 ,使得 ,使得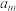 , ,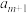 , ,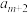 为等差数列 为等差数列 |
B. |
C.存在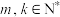 且 且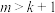 ,使得 ,使得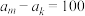 |
D.数列 的前n项和小于 的前n项和小于 |
您最近一年使用:0次
2024-01-25更新
|
407次组卷
|
4卷引用:山西省吕梁市孝义市部分学校2024届高三上学期12月月考数学试题
山西省吕梁市孝义市部分学校2024届高三上学期12月月考数学试题山西省晋中市灵石县第一中学校2024届高三上学期12月月考数学试题(已下线)期末精确押题之多选题(40题)-2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019)(已下线)考点16 几类特殊的数列模型 2024届高考数学考点总动员【练】
名校
解题方法
10 . 南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差会成等差数列.在杨辉之后,对这类高阶等差数列的研究一般称为“垛积术”",现有高阶等差数列,其前5项分别为1,4,10,20,35,则该数列的第6项为______ .
您最近一年使用:0次
2024-01-24更新
|
232次组卷
|
2卷引用:山西省运城市康杰中学2023-2024学年高二下学期开学考试数学试题



