名校
解题方法
1 . 已知数列 满足
满足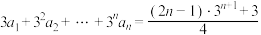 .
.
(1)求 的通项公式;
的通项公式;
(2)设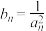 ,记
,记 的前
的前 项和为
项和为 ,求证:
,求证: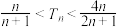 .
.
 满足
满足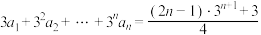 .
.(1)求
 的通项公式;
的通项公式;(2)设
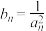 ,记
,记 的前
的前 项和为
项和为 ,求证:
,求证: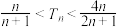 .
.
您最近一年使用:0次
2023-11-24更新
|
1521次组卷
|
7卷引用:山西省朔州市怀仁市第一中学校2023-2024学年高三上学期期中考试数学试题
解题方法
2 . 已知各项均不为0的数列 满足
满足 ,且
,且 ,则
,则
______________ .
 满足
满足 ,且
,且 ,则
,则
您最近一年使用:0次
2023-11-21更新
|
2035次组卷
|
9卷引用:山西省部分学校2024届高三上学期12月联考数学试题
山西省部分学校2024届高三上学期12月联考数学试题全国卷2024届高三一轮复习联考(三)理科数学试卷全国卷2024届高三一轮复习联考(三)文科数学试卷新疆伊犁州霍尔果斯市苏港中学2024届高三上学期第四次月考数学试题(已下线)模块三 专题1 小题入门夯实练(4) 期末终极研习室(高二人教A版)(已下线)模块二 专题8 复杂的数列递推式的探究 期末终极研习室(高二人教A版)(已下线)考点1 等差数列的定义与判断 2024届高考数学考点总动员【练】(已下线)专题04 数列的概念与等差数列(1)(已下线)专题5-2数列递推及通项应用-1
名校
解题方法
3 . 对于一个给定的数列 ,令
,令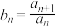 ,则数列
,则数列 称为数列
称为数列 的一阶商数列,再令
的一阶商数列,再令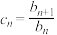 ,则数列
,则数列 是数列
是数列 的二阶商数列.已知数列
的二阶商数列.已知数列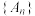 为
为 ,
, ,
, ,
,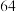 ,
, ,
, ,且它的二阶商数列是常数列,则
,且它的二阶商数列是常数列,则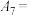 ( )
( )
 ,令
,令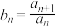 ,则数列
,则数列 称为数列
称为数列 的一阶商数列,再令
的一阶商数列,再令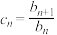 ,则数列
,则数列 是数列
是数列 的二阶商数列.已知数列
的二阶商数列.已知数列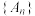 为
为 ,
, ,
, ,
,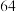 ,
, ,
, ,且它的二阶商数列是常数列,则
,且它的二阶商数列是常数列,则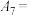 ( )
( )A.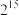 | B.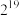 | C. | D.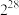 |
您最近一年使用:0次
2023-11-21更新
|
1099次组卷
|
7卷引用:山西省部分学校2024届高三上学期12月联考数学试题
4 . 已知数列 满足
满足 ,
,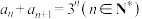 ,则下列结论正确的是( )
,则下列结论正确的是( )
 满足
满足 ,
,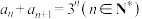 ,则下列结论正确的是( )
,则下列结论正确的是( )A. | B.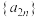 为等比数列 为等比数列 |
C.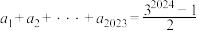 | D. |
您最近一年使用:0次
名校
解题方法
5 . 已知数列 中,
中, ,
,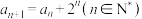 ,则下列结论正确的是( )
,则下列结论正确的是( )
 中,
中, ,
,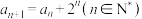 ,则下列结论正确的是( )
,则下列结论正确的是( )A. | B. 是递增数列 是递增数列 | C.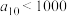 | D.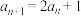 |
您最近一年使用:0次
2023-11-15更新
|
1352次组卷
|
6卷引用:山西省太原市2024届高三上学期期中数学试题
山西省太原市2024届高三上学期期中数学试题广东省揭阳市惠来同仁北实高级中学2024届高三上学期期中学业诊断数学试题福建省德化一中、永安一中、漳平一中三校协作2024届高三上学期12月联考数学试题江苏省泰州市兴化市2024届高三上学期期末适应性考试数学试题(已下线)重难点5-1 数列通项公式的求法(8题型+满分技巧+限时检测)(已下线)模块四 数列(测试)
名校
6 . 意大利著名数学家斐波拉契在研究兔子繁殖问题时,发现有这样一列数: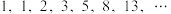 ,其中从第三项起,每一个数都等于它前面两个数的和,人们把这样的一列数组成的数列
,其中从第三项起,每一个数都等于它前面两个数的和,人们把这样的一列数组成的数列 称为“斐波拉契数列”.那么
称为“斐波拉契数列”.那么 是斐波拉契数列中的第
是斐波拉契数列中的第_____________ 项.
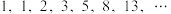 ,其中从第三项起,每一个数都等于它前面两个数的和,人们把这样的一列数组成的数列
,其中从第三项起,每一个数都等于它前面两个数的和,人们把这样的一列数组成的数列 称为“斐波拉契数列”.那么
称为“斐波拉契数列”.那么 是斐波拉契数列中的第
是斐波拉契数列中的第
您最近一年使用:0次
2023-11-13更新
|
851次组卷
|
5卷引用:山西省太原市山西大学附中2024届高三上学期12月月考(总第七次)数学试题
解题方法
7 . 定义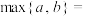
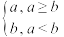 ,若数列
,若数列 的前
的前 项和为
项和为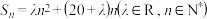 ,数列
,数列 满足
满足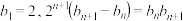
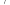 令
令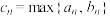 ,且
,且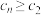 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是_______ .
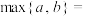
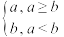 ,若数列
,若数列 的前
的前 项和为
项和为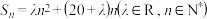 ,数列
,数列 满足
满足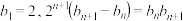
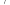 令
令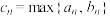 ,且
,且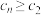 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
名校
8 . 若数列 满足
满足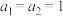 ,
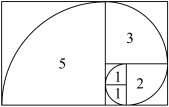
, ,则称该数列为斐波那契数列.如图所示的“黄金螺旋线”是根据斐波那契数列画出来的曲线.图中的长方形由以斐波那契数为边长的正方形拼接而成,在每个正方形中作圆心角为
,则称该数列为斐波那契数列.如图所示的“黄金螺旋线”是根据斐波那契数列画出来的曲线.图中的长方形由以斐波那契数为边长的正方形拼接而成,在每个正方形中作圆心角为 的扇形,连接起来的曲线就是“黄金螺旋线”.记以
的扇形,连接起来的曲线就是“黄金螺旋线”.记以 为边长的正方形中的扇形面积为
为边长的正方形中的扇形面积为 ,数列
,数列 的前
的前 项和为
项和为 .下列结论正确的是( )
.下列结论正确的是( )
A. | B.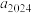 是奇数 是奇数 |
C.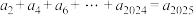 | D.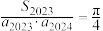 |
您最近一年使用:0次
2023-11-10更新
|
776次组卷
|
6卷引用:山西省吕梁市2024届高三上学期阶段性测试数学试题
山西省吕梁市2024届高三上学期阶段性测试数学试题宁夏回族自治区2023-2024学年高二上学期期末测试数学训练卷(三)(范围:选择性必修第二册 4.1-5.2.2)安徽省芜湖市芜湖一中2023-2024学年高二上学期12月教学质量诊断测试数学试题(已下线)考点16 几类特殊的数列模型 2024届高考数学考点总动员【练】(已下线)第4.1.2讲 数列的递推公式与前n项和-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第二、三册)黑龙江省齐齐哈尔市第八中学校2023-2024学年高二下学期3月月考数学试题
解题方法
9 . 已知等差数列 满足
满足 ,数列
,数列 的前n项和为
的前n项和为 ,且
,且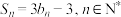 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 满足
满足 ,记
,记 的前n项和为
的前n项和为 ,若
,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 满足
满足 ,数列
,数列 的前n项和为
的前n项和为 ,且
,且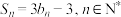 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
 满足
满足 ,记
,记 的前n项和为
的前n项和为 ,若
,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
10 . 已知数列 的前
的前 项和为
项和为 ,且满足
,且满足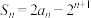 ,则下列结论正确的是( )
,则下列结论正确的是( )
 的前
的前 项和为
项和为 ,且满足
,且满足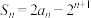 ,则下列结论正确的是( )
,则下列结论正确的是( )A. | B. |
C. | D.数列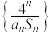 的前100项的和为 的前100项的和为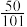 |
您最近一年使用:0次
2023-10-07更新
|
1466次组卷
|
10卷引用:山西省2024届高三上学期10月月考数学试题



