1 . 在平面直角坐标系内, ,
, ,若
,若 的面积不超过3,则满足条件的整点M个数为
的面积不超过3,则满足条件的整点M个数为________ .
 ,
, ,若
,若 的面积不超过3,则满足条件的整点M个数为
的面积不超过3,则满足条件的整点M个数为
您最近一年使用:0次
名校
解题方法
2 . 考虑这样的等腰三角形:它的三个顶点都在椭圆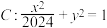 上,且其中至少有两个顶点为椭圆
上,且其中至少有两个顶点为椭圆 的顶点.这样的等腰三角形有
的顶点.这样的等腰三角形有__________ 个.
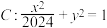 上,且其中至少有两个顶点为椭圆
上,且其中至少有两个顶点为椭圆 的顶点.这样的等腰三角形有
的顶点.这样的等腰三角形有
您最近一年使用:0次
2024高三·全国·专题练习
3 . 已知椭圆 :
: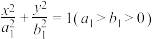 与椭圆
与椭圆 :
: 的离心率相等,
的离心率相等, 的焦点恰好为
的焦点恰好为 的顶点,圆
的顶点,圆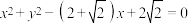 分别经过
分别经过 ,
, 的一个顶点.
的一个顶点.
(1)求 ,
, 的标准方程.
的标准方程.
(2)过 上任意一点A作
上任意一点A作 的切线与
的切线与 交于点M,N,点B是
交于点M,N,点B是 上与M,N不重合的一点,且
上与M,N不重合的一点,且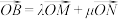 (点O为坐标原点),判断点
(点O为坐标原点),判断点 是否在定圆上.若是,求出该圆的方程;若不是,请说明理由.
是否在定圆上.若是,求出该圆的方程;若不是,请说明理由.
 :
: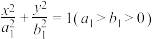 与椭圆
与椭圆 :
: 的离心率相等,
的离心率相等, 的焦点恰好为
的焦点恰好为 的顶点,圆
的顶点,圆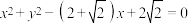 分别经过
分别经过 ,
, 的一个顶点.
的一个顶点.(1)求
 ,
, 的标准方程.
的标准方程.(2)过
 上任意一点A作
上任意一点A作 的切线与
的切线与 交于点M,N,点B是
交于点M,N,点B是 上与M,N不重合的一点,且
上与M,N不重合的一点,且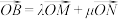 (点O为坐标原点),判断点
(点O为坐标原点),判断点 是否在定圆上.若是,求出该圆的方程;若不是,请说明理由.
是否在定圆上.若是,求出该圆的方程;若不是,请说明理由.
您最近一年使用:0次
名校
解题方法
4 . 已知圆D: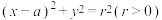 与x轴相交于A、B两点,且圆C:
与x轴相交于A、B两点,且圆C: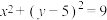 ,点
,点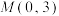 .若圆C与圆D相外切,则
.若圆C与圆D相外切,则 的最大值为( )
的最大值为( )
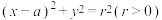 与x轴相交于A、B两点,且圆C:
与x轴相交于A、B两点,且圆C: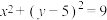 ,点
,点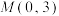 .若圆C与圆D相外切,则
.若圆C与圆D相外切,则 的最大值为( )
的最大值为( )A.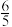 | B.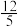 | C.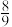 | D.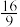 |
您最近一年使用:0次
2024·全国·模拟预测
解题方法
5 . 已知过抛物线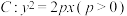 的焦点
的焦点 的直线
的直线 垂直于
垂直于 轴,且与抛物线
轴,且与抛物线 交于
交于 ,
, 两点,点
两点,点 在
在 轴上,且
轴上,且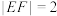 .若
.若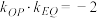 (
( 为坐标原点),则
为坐标原点),则 的准线方程为( )
的准线方程为( )
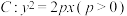 的焦点
的焦点 的直线
的直线 垂直于
垂直于 轴,且与抛物线
轴,且与抛物线 交于
交于 ,
, 两点,点
两点,点 在
在 轴上,且
轴上,且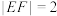 .若
.若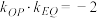 (
( 为坐标原点),则
为坐标原点),则 的准线方程为( )
的准线方程为( )A. | B. | C. | D. |
您最近一年使用:0次
2024·全国·模拟预测
解题方法
6 . 已知圆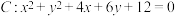 ,直线
,直线 过点
过点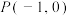 ,则“直线
,则“直线 的方程为
的方程为 ”是“直线
”是“直线 与圆
与圆 相切”的( )
相切”的( )
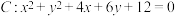 ,直线
,直线 过点
过点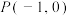 ,则“直线
,则“直线 的方程为
的方程为 ”是“直线
”是“直线 与圆
与圆 相切”的( )
相切”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
7 . 现有一“v”型的挡板如图所示,一椭圆形物件的短轴顶点被固定在A点.物件可绕A点在平面内旋转.AP间距离可调节且与两侧挡板的角度固定为60°.已知椭圆长轴长为4,短轴长为2.
(2)为了使椭圆物件能自由绕A点自由转动,AP间距离最短为多少.求出最短距离并证明其可行性.

(2)为了使椭圆物件能自由绕A点自由转动,AP间距离最短为多少.求出最短距离并证明其可行性.
您最近一年使用:0次
名校
解题方法
8 . 已知 分别为双曲线
分别为双曲线 的左、右焦点,过
的左、右焦点,过 的直线交
的直线交 于
于 ,
, (点
(点 在点
在点 的上方)两点,且
的上方)两点,且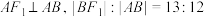 ,则
,则 的离心率可能为( )
的离心率可能为( )
 分别为双曲线
分别为双曲线 的左、右焦点,过
的左、右焦点,过 的直线交
的直线交 于
于 ,
, (点
(点 在点
在点 的上方)两点,且
的上方)两点,且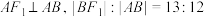 ,则
,则 的离心率可能为( )
的离心率可能为( )A.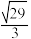 | B.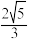 | C.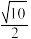 | D.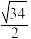 |
您最近一年使用:0次
9 . 在平面直角坐标系中,定义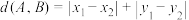 为点
为点 到点
到点 的“折线距离”.点O是坐标原点,点P在圆
的“折线距离”.点O是坐标原点,点P在圆 上,点Q在直线
上,点Q在直线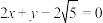 上.在这个定义下,给出下列结论:
上.在这个定义下,给出下列结论:
①若点P的横坐标为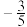 ,则
,则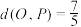 ; ②
; ②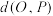 的最大值是
的最大值是
③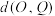 的最小值是2; ④
的最小值是2; ④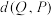 的最小值是
的最小值是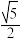
其中,所有正确结论的序号是___________ .
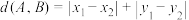 为点
为点 到点
到点 的“折线距离”.点O是坐标原点,点P在圆
的“折线距离”.点O是坐标原点,点P在圆 上,点Q在直线
上,点Q在直线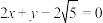 上.在这个定义下,给出下列结论:
上.在这个定义下,给出下列结论:①若点P的横坐标为
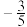 ,则
,则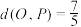 ; ②
; ②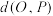 的最大值是
的最大值是
③
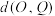 的最小值是2; ④
的最小值是2; ④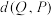 的最小值是
的最小值是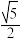
其中,所有正确结论的序号是
您最近一年使用:0次
解题方法
10 . 已知曲线C: ,则( )
,则( )
 ,则( )
,则( )| A.曲线C在第一象限为椭圆的一部分 | B.曲线C在第二象限为双曲线的一部分 |
C.直线 与曲线C有两个交点 与曲线C有两个交点 | D.直线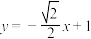 与曲线C有三个交点 与曲线C有三个交点 |
您最近一年使用:0次



