1 . 已知函数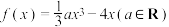 .
.
(1)若 ,求函数
,求函数 的驻点;
的驻点;
(2)讨论函数 的单调性;
的单调性;
(3)若 ,任意
,任意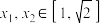 且
且 ,都有
,都有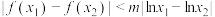 成立,求实数
成立,求实数 的取值范围.
的取值范围.
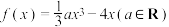 .
.(1)若
 ,求函数
,求函数 的驻点;
的驻点;(2)讨论函数
 的单调性;
的单调性;(3)若
 ,任意
,任意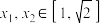 且
且 ,都有
,都有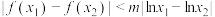 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
2 . 对于函数 ,把
,把 称为函数
称为函数 的一阶导,令
的一阶导,令 ,则将
,则将 称为函数
称为函数 的二阶导,以此类推
的二阶导,以此类推 得到n阶导.为了方便书写,我们将n阶导用
得到n阶导.为了方便书写,我们将n阶导用 表示.
表示.
(1)已知函数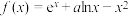 ,写出其二阶导函数并讨论其二阶导函数单调性.
,写出其二阶导函数并讨论其二阶导函数单调性.
(2)现定义一个新的数列:在 取
取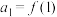 作为数列的首项,并将
作为数列的首项,并将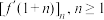 作为数列的第
作为数列的第 项.我们称该数列为
项.我们称该数列为 的“n阶导数列”
的“n阶导数列”
①若函数 (
( ),数列
),数列 是
是 的“n阶导数列”,取Tn为
的“n阶导数列”,取Tn为 的前n项积,求数列
的前n项积,求数列 的通项公式.
的通项公式.
②在我们高中阶段学过的初等函数中,是否有函数使得该函数的“n阶导数列”为严格减数列且为无穷数列,请写出它并证明此结论.(写出一个即可)
 ,把
,把 称为函数
称为函数 的一阶导,令
的一阶导,令 ,则将
,则将 称为函数
称为函数 的二阶导,以此类推
的二阶导,以此类推 得到n阶导.为了方便书写,我们将n阶导用
得到n阶导.为了方便书写,我们将n阶导用 表示.
表示.(1)已知函数
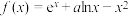 ,写出其二阶导函数并讨论其二阶导函数单调性.
,写出其二阶导函数并讨论其二阶导函数单调性.(2)现定义一个新的数列:在
 取
取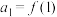 作为数列的首项,并将
作为数列的首项,并将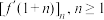 作为数列的第
作为数列的第 项.我们称该数列为
项.我们称该数列为 的“n阶导数列”
的“n阶导数列”①若函数
 (
( ),数列
),数列 是
是 的“n阶导数列”,取Tn为
的“n阶导数列”,取Tn为 的前n项积,求数列
的前n项积,求数列 的通项公式.
的通项公式.②在我们高中阶段学过的初等函数中,是否有函数使得该函数的“n阶导数列”为严格减数列且为无穷数列,请写出它并证明此结论.(写出一个即可)
您最近一年使用:0次
2023-12-16更新
|
816次组卷
|
7卷引用:上海市嘉定区2024届高三上学期质量调研数学试题
上海市嘉定区2024届高三上学期质量调研数学试题上海市普陀区长征中学2024届高三上学期10月月考数学试题广东番禺中学2023-2024学年高三第六次段考数学试题(已下线)信息必刷卷05(上海专用)(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)广东省广州市番禺中学2024届高三第六次段考数学试题
3 . 已知定义域为 的函数
的函数 .当
.当 时,若
时,若 是严格增函数,则称
是严格增函数,则称 是一个“
是一个“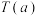 函数”.
函数”.
(1)判断函数 是否为
是否为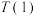 函数;
函数;
(2)是否存在实数 ,使得函数
,使得函数 是
是 函数?若存在,求实数
函数?若存在,求实数 的取值范围;否则,证明你的结论;
的取值范围;否则,证明你的结论;
(3)已知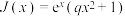 ,其中
,其中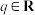 ,证明:若
,证明:若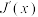 是
是 上的严格增函数,则对任意
上的严格增函数,则对任意 ,
, 都是
都是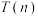 函数.
函数.
 的函数
的函数 .当
.当 时,若
时,若 是严格增函数,则称
是严格增函数,则称 是一个“
是一个“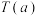 函数”.
函数”.(1)判断函数
 是否为
是否为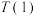 函数;
函数;(2)是否存在实数
 ,使得函数
,使得函数 是
是 函数?若存在,求实数
函数?若存在,求实数 的取值范围;否则,证明你的结论;
的取值范围;否则,证明你的结论;(3)已知
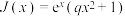 ,其中
,其中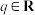 ,证明:若
,证明:若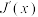 是
是 上的严格增函数,则对任意
上的严格增函数,则对任意 ,
, 都是
都是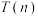 函数.
函数.
您最近一年使用:0次
解题方法
4 . 设 .
.
(1)求证:直线 与曲线
与曲线 相切;
相切;
(2)设点P在曲线 上,点Q在直线
上,点Q在直线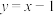 上,求
上,求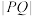 的最小值;
的最小值;
(3)若正实数a,b满足:对于任意 ,都有
,都有 ,求
,求 的最大值.
的最大值.
 .
.(1)求证:直线
 与曲线
与曲线 相切;
相切;(2)设点P在曲线
 上,点Q在直线
上,点Q在直线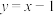 上,求
上,求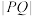 的最小值;
的最小值;(3)若正实数a,b满足:对于任意
 ,都有
,都有 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
5 . (1)设 ,
, ,求证:
,求证: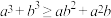 ;
;
(2)已知 ,
,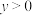 ,且
,且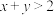 .证明:
.证明: 或
或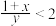 .
.
 ,
, ,求证:
,求证: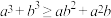 ;
;(2)已知
 ,
,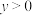 ,且
,且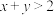 .证明:
.证明: 或
或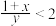 .
.
您最近一年使用:0次
6 . 设函数 的表达式为
的表达式为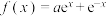 .
.
(1)求证:“ ”是“函数
”是“函数 为偶函数”的充要条件;
为偶函数”的充要条件;
(2)若 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
 的表达式为
的表达式为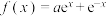 .
.(1)求证:“
 ”是“函数
”是“函数 为偶函数”的充要条件;
为偶函数”的充要条件;(2)若
 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
7 . 设函数 的定义域为
的定义域为 ,给定区间
,给定区间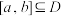 ,若存在
,若存在 ,使得
,使得 ,则称函数
,则称函数 为区间
为区间 上的“均值函数”,
上的“均值函数”, 为函数
为函数 的“均值点”.
的“均值点”.
(1)试判断函数 是否为区间
是否为区间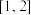 上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;
上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;
(2)已知函数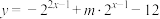 是区间
是区间 上的“均值函数”,求实数
上的“均值函数”,求实数 的取值范围;
的取值范围;
(3)若函数 (常数
(常数 )是区间
)是区间 上的“均值函数”,且
上的“均值函数”,且 为其“均值点”.将区间
为其“均值点”.将区间 任意划分成
任意划分成 (
(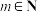 )份,设分点的横坐标从小到大依次为
)份,设分点的横坐标从小到大依次为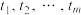 ,记
,记 ,
,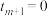 ,
, .再将区间
.再将区间 等分成
等分成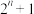 (
( )份,设等分点的横坐标从小到大依次为
)份,设等分点的横坐标从小到大依次为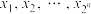 ,记
,记 .求使得
.求使得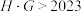 的最小整数
的最小整数 的值.
的值.
 的定义域为
的定义域为 ,给定区间
,给定区间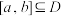 ,若存在
,若存在 ,使得
,使得 ,则称函数
,则称函数 为区间
为区间 上的“均值函数”,
上的“均值函数”, 为函数
为函数 的“均值点”.
的“均值点”.(1)试判断函数
 是否为区间
是否为区间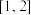 上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;
上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;(2)已知函数
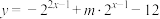 是区间
是区间 上的“均值函数”,求实数
上的“均值函数”,求实数 的取值范围;
的取值范围;(3)若函数
 (常数
(常数 )是区间
)是区间 上的“均值函数”,且
上的“均值函数”,且 为其“均值点”.将区间
为其“均值点”.将区间 任意划分成
任意划分成 (
(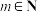 )份,设分点的横坐标从小到大依次为
)份,设分点的横坐标从小到大依次为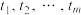 ,记
,记 ,
,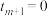 ,
, .再将区间
.再将区间 等分成
等分成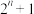 (
( )份,设等分点的横坐标从小到大依次为
)份,设等分点的横坐标从小到大依次为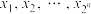 ,记
,记 .求使得
.求使得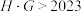 的最小整数
的最小整数 的值.
的值.
您最近一年使用:0次
2023-12-14更新
|
483次组卷
|
4卷引用:上海市金山区2024届高三上学期质量监控数学试题
上海市金山区2024届高三上学期质量监控数学试题(已下线)专题09 导数(三大类型题)15区新题速递(已下线)专题03 函数(三大类型题)15区新题速递广东省广州市第二中学2023-2024学年高二下学期期中考试数学试题
解题方法
8 . 若函数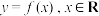 的导函数
的导函数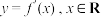 是以
是以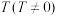 为周期的函数,则称函数
为周期的函数,则称函数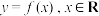 具有“
具有“ 性质”.
性质”.
(1)试判断函数
 和
和 是否具有“
是否具有“ 性质”,并说明理由;
性质”,并说明理由;(2)已知函数
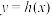 ,其中
,其中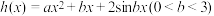 具有“
具有“ 性质”,求函数
性质”,求函数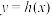 在
在 上的极小值点;
上的极小值点;(3)若函数
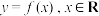 具有“
具有“ 性质”,且存在实数
性质”,且存在实数 使得对任意
使得对任意 都有
都有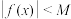 成立,求证:
成立,求证: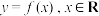 为周期函数.
为周期函数.(可用结论:若函数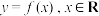 的导函数满足
的导函数满足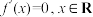 ,则
,则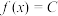 (常数).)
(常数).)
您最近一年使用:0次
9 . 已知函数 ,
,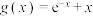 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(1)求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(2)设函数 ,
,
①若 ,求函数
,求函数 的单调区间,并写出函数
的单调区间,并写出函数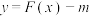 有三个零点时实数
有三个零点时实数 的取值范围;
的取值范围;
②当 时,
时,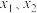 分别为函数
分别为函数 的极大值点和极小值点,且不等式
的极大值点和极小值点,且不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 ,
,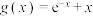 ,其中
,其中 为自然对数的底数.
为自然对数的底数.(1)求函数
 的图象在点
的图象在点 处的切线方程;
处的切线方程;(2)设函数
 ,
,①若
 ,求函数
,求函数 的单调区间,并写出函数
的单调区间,并写出函数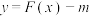 有三个零点时实数
有三个零点时实数 的取值范围;
的取值范围;②当
 时,
时,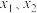 分别为函数
分别为函数 的极大值点和极小值点,且不等式
的极大值点和极小值点,且不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
10 . 已知有穷等差数列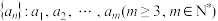 的公差d大于零.
的公差d大于零.
(1)证明: 不是等比数列;
不是等比数列;
(2)是否存在指数函数  满足:
满足: 在
在 处的切线的交
处的切线的交 轴于
轴于 ,
, 在
在 处的切线的交
处的切线的交 轴于
轴于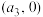 ,…,
,…, 在
在 处的切线的交
处的切线的交 轴于
轴于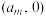 ?若存在,请写出函数
?若存在,请写出函数 的表达式,并说明理由;若不存在,也请说明理由;
的表达式,并说明理由;若不存在,也请说明理由;
(3)若数列 中所有项按照某种顺序排列后可以构成等比数列
中所有项按照某种顺序排列后可以构成等比数列 ,求出所有可能的m的取值.
,求出所有可能的m的取值.
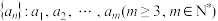 的公差d大于零.
的公差d大于零.(1)证明:
 不是等比数列;
不是等比数列;(2)是否存在
 满足:
满足: 在
在 处的切线的交
处的切线的交 轴于
轴于 ,
, 在
在 处的切线的交
处的切线的交 轴于
轴于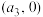 ,…,
,…, 在
在 处的切线的交
处的切线的交 轴于
轴于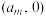 ?若存在,请写出函数
?若存在,请写出函数 的表达式,并说明理由;若不存在,也请说明理由;
的表达式,并说明理由;若不存在,也请说明理由;(3)若数列
 中所有项按照某种顺序排列后可以构成等比数列
中所有项按照某种顺序排列后可以构成等比数列 ,求出所有可能的m的取值.
,求出所有可能的m的取值.
您最近一年使用:0次
2023-12-13更新
|
664次组卷
|
5卷引用:上海市青浦区2024届高三上学期期终学业质量调研数学试题
上海市青浦区2024届高三上学期期终学业质量调研数学试题(已下线)专题05 数列(四大类型题)15区新题速递(已下线)专题09 导数(三大类型题)15区新题速递(已下线)数学(上海卷01)2024届高三新高考改革数学适应性练习(6)(九省联考题型)



