1 . 已知①设函数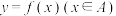 的值域是
的值域是 ,对于
,对于 中的每个
中的每个 ,若函数
,若函数 在每一处
在每一处 都等于它对应的
都等于它对应的 ,这样的函数
,这样的函数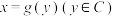 叫做函数
叫做函数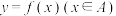 的反函数,记作
的反函数,记作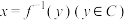 ,我们习惯记自变量为
,我们习惯记自变量为 ,因此
,因此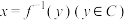 可改成
可改成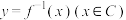 即为原函数的反函数.易知
即为原函数的反函数.易知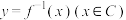 与
与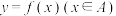 互为反函数,且
互为反函数,且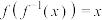 .如
.如 的反函数是
的反函数是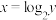 可改写成
可改写成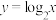 即为
即为 的反函数,
的反函数,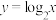 与
与 互为反函数.②
互为反函数.② 是定义在
是定义在 且取值于
且取值于 的一个函数,定义
的一个函数,定义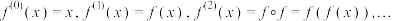
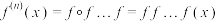 ,则称
,则称 是函数
是函数 在
在 上的
上的 次迭代.例如
次迭代.例如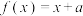 ,则
,则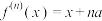 .对于一些相对复杂的函数,为求出其
.对于一些相对复杂的函数,为求出其 次迭代函数,我们引入如下一种关系:对于给定的函数
次迭代函数,我们引入如下一种关系:对于给定的函数 和
和 ,若函数
,若函数 的反函数
的反函数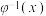 存在,且有
存在,且有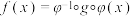 ,称
,称 与
与 关于
关于 相似,记作
相似,记作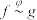 ,其中
,其中 称为桥函数,桥函数满足以下性质:
称为桥函数,桥函数满足以下性质:
(i)若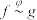 ,则
,则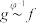
(ii)若 为
为 的一个不动点,即
的一个不动点,即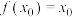 ,则
,则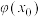 为
为 的一个不动点.
的一个不动点.
(1)若函数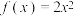 ,求
,求 (写出结果即可)
(写出结果即可)
(2)证明:若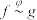 ,则
,则 .
.
(3)若函数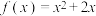 ,求
,求 (桥函数可选取
(桥函数可选取 ),若
),若 ,试选取恰当桥函数,计算
,试选取恰当桥函数,计算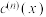 .
.
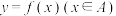 的值域是
的值域是 ,对于
,对于 中的每个
中的每个 ,若函数
,若函数 在每一处
在每一处 都等于它对应的
都等于它对应的 ,这样的函数
,这样的函数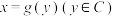 叫做函数
叫做函数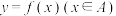 的反函数,记作
的反函数,记作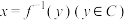 ,我们习惯记自变量为
,我们习惯记自变量为 ,因此
,因此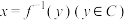 可改成
可改成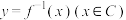 即为原函数的反函数.易知
即为原函数的反函数.易知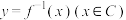 与
与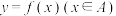 互为反函数,且
互为反函数,且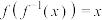 .如
.如 的反函数是
的反函数是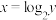 可改写成
可改写成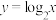 即为
即为 的反函数,
的反函数,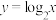 与
与 互为反函数.②
互为反函数.② 是定义在
是定义在 且取值于
且取值于 的一个函数,定义
的一个函数,定义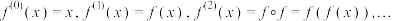
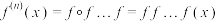 ,则称
,则称 是函数
是函数 在
在 上的
上的 次迭代.例如
次迭代.例如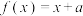 ,则
,则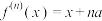 .对于一些相对复杂的函数,为求出其
.对于一些相对复杂的函数,为求出其 次迭代函数,我们引入如下一种关系:对于给定的函数
次迭代函数,我们引入如下一种关系:对于给定的函数 和
和 ,若函数
,若函数 的反函数
的反函数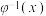 存在,且有
存在,且有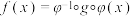 ,称
,称 与
与 关于
关于 相似,记作
相似,记作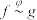 ,其中
,其中 称为桥函数,桥函数满足以下性质:
称为桥函数,桥函数满足以下性质:(i)若
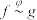 ,则
,则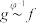
(ii)若
 为
为 的一个不动点,即
的一个不动点,即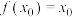 ,则
,则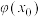 为
为 的一个不动点.
的一个不动点.(1)若函数
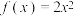 ,求
,求 (写出结果即可)
(写出结果即可)(2)证明:若
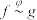 ,则
,则 .
.(3)若函数
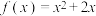 ,求
,求 (桥函数可选取
(桥函数可选取 ),若
),若 ,试选取恰当桥函数,计算
,试选取恰当桥函数,计算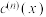 .
.
您最近一年使用:0次
名校
2 . 下列说法错误的个数为( )
①已知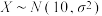 ,若
,若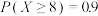 ,则
,则
②已知 ,则
,则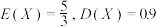
③投掷一枚均匀的硬币5次,已知正面向上不少于3次,则出现5次正面向上的概率为
①已知
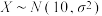 ,若
,若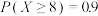 ,则
,则
②已知
 ,则
,则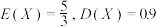
③投掷一枚均匀的硬币5次,已知正面向上不少于3次,则出现5次正面向上的概率为

| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
3 . 当 且
且 时,
时,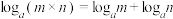 对一切
对一切 ,
, 恒成立.学生小刚在研究对数运算时,发现有这么一个等式
恒成立.学生小刚在研究对数运算时,发现有这么一个等式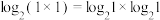 ,带着好奇,他进一步对
,带着好奇,他进一步对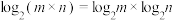 进行深入研究.
进行深入研究.
(1)若正数 ,
, 满足
满足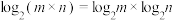 ,当
,当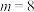 时,求
时,求 的值;
的值;
(2)除整数对 ,请再举出一个整数对
,请再举出一个整数对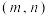 满足
满足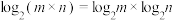 ;
;
(3)证明:当 时,只有一对正整数对
时,只有一对正整数对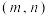 使得等式
使得等式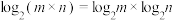 成立.
成立.
 且
且 时,
时,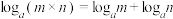 对一切
对一切 ,
, 恒成立.学生小刚在研究对数运算时,发现有这么一个等式
恒成立.学生小刚在研究对数运算时,发现有这么一个等式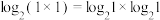 ,带着好奇,他进一步对
,带着好奇,他进一步对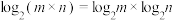 进行深入研究.
进行深入研究.(1)若正数
 ,
, 满足
满足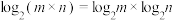 ,当
,当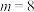 时,求
时,求 的值;
的值;(2)除整数对
 ,请再举出一个整数对
,请再举出一个整数对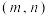 满足
满足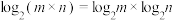 ;
;(3)证明:当
 时,只有一对正整数对
时,只有一对正整数对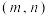 使得等式
使得等式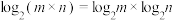 成立.
成立.
您最近一年使用:0次
2024-06-08更新
|
195次组卷
|
2卷引用:浙江省培优联盟2023-2024学年高一下学期5月联考数学试题
名校
解题方法
4 . 对于 ,定义
,定义 ,
,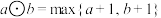 ,其中
,其中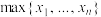 为
为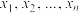 中最大的数,例如:
中最大的数,例如: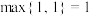 ,
,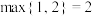 ,
, . 给定正整数
. 给定正整数 ,根据以上内容,对于
,根据以上内容,对于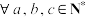 ,请回答下列问题:
,请回答下列问题:
(1)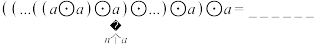 (用
(用 和
和 表示);
表示);
(2)满足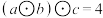 的有序数对
的有序数对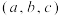 有多少个?
有多少个?
(3)满足 的有序数对
的有序数对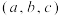 有多少个?
有多少个?
(4)满足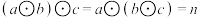 的有序数对
的有序数对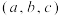 有多少个?
有多少个?
 ,定义
,定义 ,
,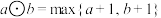 ,其中
,其中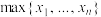 为
为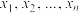 中最大的数,例如:
中最大的数,例如: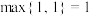 ,
,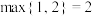 ,
, . 给定正整数
. 给定正整数 ,根据以上内容,对于
,根据以上内容,对于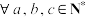 ,请回答下列问题:
,请回答下列问题:(1)
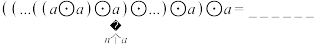 (用
(用 和
和 表示);
表示);(2)满足
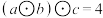 的有序数对
的有序数对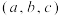 有多少个?
有多少个?(3)满足
 的有序数对
的有序数对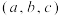 有多少个?
有多少个?(4)满足
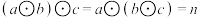 的有序数对
的有序数对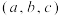 有多少个?
有多少个?
您最近一年使用:0次
名校
5 . 水平相当的甲、乙、丙三人进行乒乓球擂台赛,每轮比赛都采用3局2胜制(即先贏2局者胜),首轮由甲乙两人开始,丙轮空;第二轮由首轮的胜者与丙之间进行,首轮的负者轮空,依照这样的规则无限地继续下去.
(1)求甲在第三轮获胜的条件下,第二轮也获胜的概率;
(2)求第 轮比赛甲轮空的概率;
轮比赛甲轮空的概率;
(3)按照以上规则,求前六轮比赛中甲获胜局数的期望.
(1)求甲在第三轮获胜的条件下,第二轮也获胜的概率;
(2)求第
 轮比赛甲轮空的概率;
轮比赛甲轮空的概率;(3)按照以上规则,求前六轮比赛中甲获胜局数的期望.
您最近一年使用:0次
名校
解题方法
6 . 有一款闯关游戏,其规则如下:一颗棋子位于数轴原点 处,若掷出的骰子大于或者等于3,则棋子向右移动一个单位(从0移动到1),若掷出的骰子小于或者等于2,则棋子向右移动两个单位(从0移动到2),若棋子移动到99处,则“闯关失败”,若棋子移动到100处,则“闯关成功”,无论“闯关失败”或者“闯关成功”都将停止游戏,记棋子在坐标
处,若掷出的骰子大于或者等于3,则棋子向右移动一个单位(从0移动到1),若掷出的骰子小于或者等于2,则棋子向右移动两个单位(从0移动到2),若棋子移动到99处,则“闯关失败”,若棋子移动到100处,则“闯关成功”,无论“闯关失败”或者“闯关成功”都将停止游戏,记棋子在坐标 处的概率为
处的概率为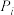 .
.
(1)求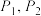 ;
;
(2)求证: 为等比数列(其中
为等比数列(其中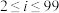 ),并求出
),并求出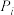 ;
;
(3)若有5人同时参加此游戏,记随机变量 为“闯关成功”的人数,求
为“闯关成功”的人数,求 (结果保留两位有效数字).
(结果保留两位有效数字).
 处,若掷出的骰子大于或者等于3,则棋子向右移动一个单位(从0移动到1),若掷出的骰子小于或者等于2,则棋子向右移动两个单位(从0移动到2),若棋子移动到99处,则“闯关失败”,若棋子移动到100处,则“闯关成功”,无论“闯关失败”或者“闯关成功”都将停止游戏,记棋子在坐标
处,若掷出的骰子大于或者等于3,则棋子向右移动一个单位(从0移动到1),若掷出的骰子小于或者等于2,则棋子向右移动两个单位(从0移动到2),若棋子移动到99处,则“闯关失败”,若棋子移动到100处,则“闯关成功”,无论“闯关失败”或者“闯关成功”都将停止游戏,记棋子在坐标 处的概率为
处的概率为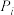 .
.(1)求
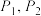 ;
;(2)求证:
 为等比数列(其中
为等比数列(其中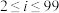 ),并求出
),并求出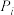 ;
;(3)若有5人同时参加此游戏,记随机变量
 为“闯关成功”的人数,求
为“闯关成功”的人数,求 (结果保留两位有效数字).
(结果保留两位有效数字).
您最近一年使用:0次
名校
7 . 为贯彻落实《健康中国行动(2023-2030年)》、《关于全面加强和改进新时代学校体育工作的意见》等文件精神,某高中学校学生发展中心随机抽查了100名学生,其中男生与女生人数之比为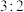 ,并对他们进行了“是否喜欢体育运动”的问卷调查,得到如下统计结果:
,并对他们进行了“是否喜欢体育运动”的问卷调查,得到如下统计结果:
(1)请根据要求完成 列联表,并根据独立性检验,判断是否有
列联表,并根据独立性检验,判断是否有 的把握认为“是否喜欢体育运动”与性别有关;
的把握认为“是否喜欢体育运动”与性别有关;
(2)为了了解学生不喜欢体育运动的原因,从上述不喜欢体育运动的同学中随机选3位同学进行咨询,所选的3人中已知至少有两位是男生的条件下,求另外一位是女生的概率.
参考公式: .
.
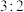 ,并对他们进行了“是否喜欢体育运动”的问卷调查,得到如下统计结果:
,并对他们进行了“是否喜欢体育运动”的问卷调查,得到如下统计结果:| 性别 | 体育运动 | 合计 | |
| 喜欢 | 不喜欢 | ||
| 男生 | 50 | ||
| 女生 | 15 | ||
| 合计 | |||
 列联表,并根据独立性检验,判断是否有
列联表,并根据独立性检验,判断是否有 的把握认为“是否喜欢体育运动”与性别有关;
的把握认为“是否喜欢体育运动”与性别有关;(2)为了了解学生不喜欢体育运动的原因,从上述不喜欢体育运动的同学中随机选3位同学进行咨询,所选的3人中已知至少有两位是男生的条件下,求另外一位是女生的概率.
参考公式:
 .
. | 0.10 | 0.05 | 0.01 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
8 . 某班上有5名同学相约周末去公园拍照,这5名同学站成一排,其中甲、乙两名同学要求站在一起,丙同学不站在两端,不同的安排方法数有( )
| A.24 | B.12 | C.48 | D.36 |
您最近一年使用:0次
名校
9 . 对两个变量 和
和 进行回归分析,则下列说法正确的是( )
进行回归分析,则下列说法正确的是( )
 和
和 进行回归分析,则下列说法正确的是( )
进行回归分析,则下列说法正确的是( )A.在比较两个回归模型的拟合程度时,决定系数 越大,拟合效果越好 越大,拟合效果越好 |
B.若变量 和 和 具有线性相关关系,则回归直线方程 具有线性相关关系,则回归直线方程 至少经过样本点的其中一个点 至少经过样本点的其中一个点 |
C.建立两个回归模型,模型1的线性相关系数 ,模型2的线性相关系数 ,模型2的线性相关系数 ,则模型1的线性相关性更强 ,则模型1的线性相关性更强 |
| D.残差图中的点均匀地分布在一条水平的带状区域内,该带状区域宽度越窄,模型的拟合效果越好 |
您最近一年使用:0次
名校
解题方法
10 . 已知函数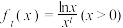 ,其中
,其中 ,则下列选项正确的是( )
,则下列选项正确的是( )
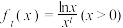 ,其中
,其中 ,则下列选项正确的是( )
,则下列选项正确的是( )A.若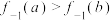 ,则 ,则 |
B. |
C.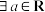 ,使 ,使 有两解,则 有两解,则 |
D.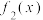 有最大值 有最大值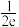 |
您最近一年使用:0次



