1 . 我国元代数学家朱世杰在他的《四元玉鉴》一书中对高阶等差数列求和有精深的研究,即“垛积术”.对于数列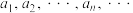 ,①,从第二项起,每一项与它前面相邻一项的差构成数列
,①,从第二项起,每一项与它前面相邻一项的差构成数列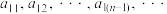 ,②,称该数列②为数列①的一阶差分数列,其中
,②,称该数列②为数列①的一阶差分数列,其中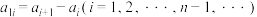 ;对于数列②,从第二项起,每一项与它前面相邻一项的差构成数列
;对于数列②,从第二项起,每一项与它前面相邻一项的差构成数列 ,③,称该数列③为数列①的二阶差分数列,其中
,③,称该数列③为数列①的二阶差分数列,其中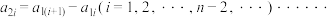 按照上述办法,第
按照上述办法,第 次得到数列
次得到数列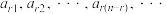 ,④,则称数列④为数列①的
,④,则称数列④为数列①的 阶差分数列,其中
阶差分数列,其中 ,若数列
,若数列 的
的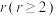 阶差分数列是非零常数列,则称数列
阶差分数列是非零常数列,则称数列 为
为 阶等差数列(或高阶等差数列).
阶等差数列(或高阶等差数列).
(1)若高阶等差数列 为
为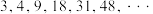 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若 阶等差数列
阶等差数列 的通项公式
的通项公式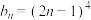 .
.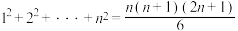 .
.
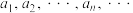 ,①,从第二项起,每一项与它前面相邻一项的差构成数列
,①,从第二项起,每一项与它前面相邻一项的差构成数列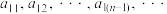 ,②,称该数列②为数列①的一阶差分数列,其中
,②,称该数列②为数列①的一阶差分数列,其中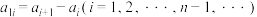 ;对于数列②,从第二项起,每一项与它前面相邻一项的差构成数列
;对于数列②,从第二项起,每一项与它前面相邻一项的差构成数列 ,③,称该数列③为数列①的二阶差分数列,其中
,③,称该数列③为数列①的二阶差分数列,其中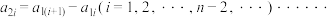 按照上述办法,第
按照上述办法,第 次得到数列
次得到数列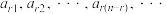 ,④,则称数列④为数列①的
,④,则称数列④为数列①的 阶差分数列,其中
阶差分数列,其中 ,若数列
,若数列 的
的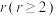 阶差分数列是非零常数列,则称数列
阶差分数列是非零常数列,则称数列 为
为 阶等差数列(或高阶等差数列).
阶等差数列(或高阶等差数列).(1)若高阶等差数列
 为
为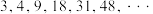 ,求数列
,求数列 的通项公式;
的通项公式;(2)若
 阶等差数列
阶等差数列 的通项公式
的通项公式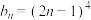 .
.(ⅰ)求 的值;
的值;
(ⅱ)求数列 的前
的前 项和
项和 .
.
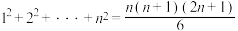 .
.
您最近一年使用:0次
2 . 随着大数据时代来临,数据传输安全问题引起了人们的高度关注,国际上常用的数据加密算法通常有AES、DES、RSA等,不同算法密钥长度也不同,其中RSA的密钥长度较长,用于传输敏感数据.在密码学领域,欧拉函数是非常重要的,其中最著名的应用就是在RSA加密算法中的应用.设p,q是两个正整数,若p,q的最大公约数是1,则称p,q互素.对于任意正整数n,欧拉函数是不超过n且与n互素的正整数的个数,记为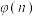 .
.
(1)试求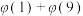 ,
, 的值;
的值;
(2)设p,q是两个不同的素数,试用p,k表示 (
(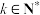 ),并探究
),并探究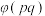 与
与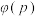 和
和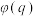 的关系;
的关系;
(3)设数列 的通项公式为
的通项公式为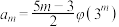 (
( ),求该数列的前m项的和
),求该数列的前m项的和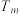 .
.
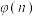 .
.(1)试求
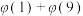 ,
, 的值;
的值;(2)设p,q是两个不同的素数,试用p,k表示
 (
(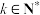 ),并探究
),并探究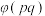 与
与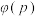 和
和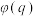 的关系;
的关系;(3)设数列
 的通项公式为
的通项公式为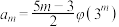 (
( ),求该数列的前m项的和
),求该数列的前m项的和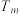 .
.
您最近一年使用:0次
3 . 在 个数码
个数码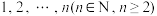 构成的一个排列
构成的一个排列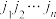 中,若一个较大的数码排在一个较小的数码的前面,则称它们构成逆序(例如
中,若一个较大的数码排在一个较小的数码的前面,则称它们构成逆序(例如 ,则
,则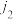 与
与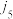 构成逆序),这个排列的所有逆序的总个数称为这个排列的逆序数,记为
构成逆序),这个排列的所有逆序的总个数称为这个排列的逆序数,记为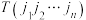 ,例如,
,例如,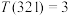 .
.
(1)计算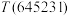 ;
;
(2)设数列 满足
满足 ,
, ,求
,求 的通项公式;
的通项公式;
(3)设排列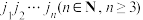 满足
满足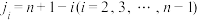 ,
, ,
, ,
,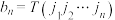 ,
,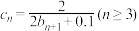 ,证明:
,证明: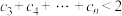 .
.
 个数码
个数码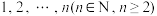 构成的一个排列
构成的一个排列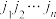 中,若一个较大的数码排在一个较小的数码的前面,则称它们构成逆序(例如
中,若一个较大的数码排在一个较小的数码的前面,则称它们构成逆序(例如 ,则
,则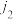 与
与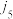 构成逆序),这个排列的所有逆序的总个数称为这个排列的逆序数,记为
构成逆序),这个排列的所有逆序的总个数称为这个排列的逆序数,记为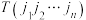 ,例如,
,例如,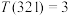 .
.(1)计算
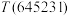 ;
;(2)设数列
 满足
满足 ,
, ,求
,求 的通项公式;
的通项公式;(3)设排列
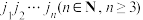 满足
满足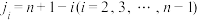 ,
, ,
, ,
,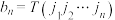 ,
,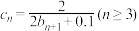 ,证明:
,证明: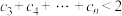 .
.
您最近一年使用:0次
名校
4 . 马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.其数学定义为:假设我们的序列状态是……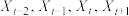 ,…,那么
,…,那么 时刻的状态的条件概率仅依赖前一状态
时刻的状态的条件概率仅依赖前一状态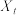 ,即
,即 .
.
现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.
假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为 ,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为
,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为 ,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:记赌徒的本金为
,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:记赌徒的本金为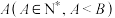 一种是赌金达到预期的B元,赌徒停止赌博;另一种是赌徒输光本金后,赌徒可以向赌场借钱,最多借A元,再次输光后赌场不再借钱给赌徒.赌博过程如图的数轴所示.
一种是赌金达到预期的B元,赌徒停止赌博;另一种是赌徒输光本金后,赌徒可以向赌场借钱,最多借A元,再次输光后赌场不再借钱给赌徒.赌博过程如图的数轴所示.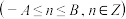 时,
时,最终欠债 A元(可以记为该赌徒手中有 
元)概率为 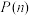 ,请回答下列问题:
,请回答下列问题:
(1)请直接写出 与
与 的数值.
的数值.
(2)证明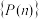 是一个等差数列,并写出公差d.
是一个等差数列,并写出公差d.
(3)当 时,分别计算
时,分别计算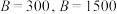 时,
时, 的数值,论述当B持续增大时,
的数值,论述当B持续增大时, 的统计含义.
的统计含义.
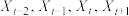 ,…,那么
,…,那么 时刻的状态的条件概率仅依赖前一状态
时刻的状态的条件概率仅依赖前一状态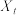 ,即
,即 .
.现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.
假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为
 ,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为
,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为 ,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:记赌徒的本金为
,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:记赌徒的本金为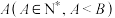 一种是赌金达到预期的B元,赌徒停止赌博;另一种是赌徒输光本金后,赌徒可以向赌场借钱,最多借A元,再次输光后赌场不再借钱给赌徒.赌博过程如图的数轴所示.
一种是赌金达到预期的B元,赌徒停止赌博;另一种是赌徒输光本金后,赌徒可以向赌场借钱,最多借A元,再次输光后赌场不再借钱给赌徒.赌博过程如图的数轴所示.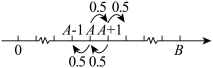
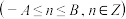 时,
时,
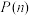 ,请回答下列问题:
,请回答下列问题:(1)请直接写出
 与
与 的数值.
的数值.(2)证明
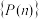 是一个等差数列,并写出公差d.
是一个等差数列,并写出公差d.(3)当
 时,分别计算
时,分别计算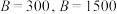 时,
时, 的数值,论述当B持续增大时,
的数值,论述当B持续增大时, 的统计含义.
的统计含义.
您最近一年使用:0次
2024-04-17更新
|
1243次组卷
|
3卷引用:江西省南昌市第十九中学2024届高三下学期第四次模拟考试数学试卷
江西省南昌市第十九中学2024届高三下学期第四次模拟考试数学试卷辽宁省实验中学2023-2024学年高二下学期3月月考数学试题(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)
名校
解题方法
5 . “费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当 的三个内角均小于
的三个内角均小于 时,使得
时,使得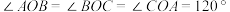 的点
的点 即为费马点;当
即为费马点;当 有一个内角大于或等于
有一个内角大于或等于 时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知
时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且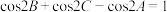
(1)求 ;
;
(2)若 ,设点
,设点 为
为 的费马点,求
的费马点,求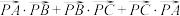 ;
;
(3)设点 为
为 的费马点,
的费马点,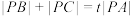 ,求实数
,求实数 的最小值.
的最小值.
 的三个内角均小于
的三个内角均小于 时,使得
时,使得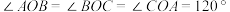 的点
的点 即为费马点;当
即为费马点;当 有一个内角大于或等于
有一个内角大于或等于 时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知
时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且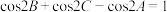
(1)求
 ;
;(2)若
 ,设点
,设点 为
为 的费马点,求
的费马点,求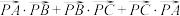 ;
;(3)设点
 为
为 的费马点,
的费马点,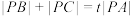 ,求实数
,求实数 的最小值.
的最小值.
您最近一年使用:0次
2024-03-03更新
|
4546次组卷
|
38卷引用:江西省南昌市第十中学2023-2024学年高一下学期第二次月考数学试题
江西省南昌市第十中学2023-2024学年高一下学期第二次月考数学试题重庆市求精中学校2023-2024学年高二下学期阶段测试数学试题2024届高三新高考改革数学适应性练习(7)(九省联考题型)(已下线)第六章 本章综合--方法提升应用【第三练】“上好三节课,做好三套题“高中数学素养晋级之路河北省沧州市泊头市第一中学2023-2024学年高一下学期3月月考数学试题云南省昆明市五华区云南师范大学附属中学2023-2024学年高一下学期3月月考数学试题湖南省长沙市明德中学2023-2024学年高一下学期3月月考数学试题山东省实验中学2023-2024学年高一下学期第一次阶段测试(3月)数学试题海南省海口市海南中学2023-2024学年高一下学期3月月考数学试题(已下线)模块五 专题四 全真能力模拟2(高一期中模拟)重庆市乌江新高考协作体2023-2024学年高一下学期第一阶段学业质量联合调研抽测(4月)数学试题河北省衡水市郑口中学2023-2024学年高一下学期质检一数学试题广东省中山市桂山中学2023-2024学年高一下学期第一次段考检测数学试题甘肃省张掖中学2023-2024学年高一下学期4月月考数学试卷四川省射洪中学校2023-2024学年高一强基班下学期第一次学月考试(4月)数学试题河南省郑州市基石中学2023-2024学年高一下学期4月月考数学试题广东省东莞市东莞中学松山湖学校2023-2024学年高一下学期第一次段考数学试题安徽省皖北名校2023-2024学年高一下学期阶段性联考数学试卷广东省深圳外国语学校2023-2024学年高一下学期4月月考数学试卷吉林省长春市十一高中2023-2024学年高一下学期4月月考数学试题湖北省武汉市第六中学2023-2024学年高一下学期4月月考数学试卷广东省江门市第一中学2023-2024学年高一下学期第一次阶段考试数学试题湖南省慈利县第一中学2023-2024学年高一下学期期中考试数学试题单元测试A卷——第六章?平面向量及其应用上海市第二中学2023-2024学年高一下学期期中考试数学试卷四川省南充市嘉陵第一中学2023-2024学年高一下学期4月期中考试数学试题山东省淄博市高青县第一中学2023-2024学年高一下学期期中考试数学试题福建省浦城第一中学2023-2024学年高一下学期4月期中考试数学试题上海市宜川中学2023-2024学年高一下学期期中考试数学试题江苏省南京市中华中学2023-2024学年高一下学期期中联考数学试题福建省厦门市湖滨中学2023-2024学年高一下学期期中考试数学试题广东省广州市白云艺术中学2023-2024学年高一下学期期中数学试题广东省广州市第六十五中学2023-2024学年高一下学期期中考试数学试卷重庆市涪陵第五中学校2023-2024学年高一下学期第一次月考数学试题山东省青岛市第五十八中学2023-2024学年高一下学期期中考试数学试题福建省莆田第八中学2023-2024学年高一下学期期中考试数学试卷辽宁省沈阳市五校协作体2023-2024学年高一下学期5月期中考试数学试题山东省聊城一中2023-2024学年下学期期中考试高一数学试题
6 . 固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程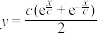 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数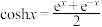 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数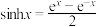 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.
(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论: _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);
(2)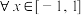 ,不等式
,不等式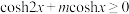 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若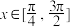 ,试比较
,试比较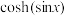 与
与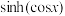 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
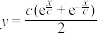 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数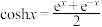 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数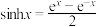 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论:
 _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);(2)
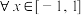 ,不等式
,不等式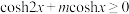 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
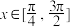 ,试比较
,试比较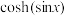 与
与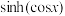 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
您最近一年使用:0次
2024-01-27更新
|
958次组卷
|
10卷引用:江西省上饶市横峰县横峰中学2023-2024学年高一下学期期中考试数学试卷
江西省上饶市横峰县横峰中学2023-2024学年高一下学期期中考试数学试卷福建省宁德市2023-2024学年高一上学期1月期末质量检测数学试题重庆市缙云教育联盟2024届高三下学期2月月度质量检测数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)讲河南省名校联盟2023-2024学年高一下学期3月测试数学试题(已下线)第八章:向量的数量积与三角恒等变换章末重点题型复习(2)-同步精品课堂(人教B版2019必修第三册)河南省信阳市信阳高级中学2023-2024学年高一下学期3月月考(一)数学试题(已下线)第8章:向量的数量积与三角恒等变换章末综合检测卷(新题型)-【帮课堂】(人教B版2019必修第三册)(已下线)专题04 三角函数恒等变形综合大题归类 -期末考点大串讲(苏教版(2019))(已下线)专题08 期末必刷解答题专题训练的7种常考题型归类-期末真题分类汇编(北师大版2019必修第二册)
名校
解题方法
7 . 国家主席习近平在2024年新年贺词中指出,“2023年,我们接续奋斗、砥砺前行,经历了风雨洗礼,看到了美丽风景,取得了沉甸甸的收获”“粮食生产“二十连丰,绿水青山成色更足,乡村振兴展现新气象”.某乡镇响应国家号召,计划修建如图所示的矩形花园,其占地面积为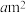 ,花园四周修建通道,花园一边长为
,花园四周修建通道,花园一边长为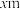 ,且
,且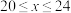 .
.
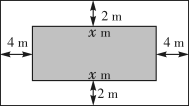
(1)设花园及周边通道的总占地面积为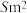 ,试求
,试求 与
与 的函数解析式;
的函数解析式;
(2)当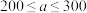 时,试求
时,试求 的最小值.
的最小值.
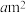 ,花园四周修建通道,花园一边长为
,花园四周修建通道,花园一边长为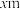 ,且
,且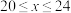 .
.
(1)设花园及周边通道的总占地面积为
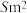 ,试求
,试求 与
与 的函数解析式;
的函数解析式;(2)当
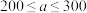 时,试求
时,试求 的最小值.
的最小值.
您最近一年使用:0次
2024-01-26更新
|
219次组卷
|
2卷引用:江西省上饶市广丰中学2023-2024学年高一上学期期末数学试题
解题方法
8 . 某班级在迎新春活动中进行抽卡活动,不透明的卡箱中共有“福”“迎”“春”卡各两张,“龙”卡三张.每个学生从卡箱中随机抽取4张卡片,其中抽到“龙”卡获得2分,抽到其他卡均获得1分,若抽中“福”“龙”“迎”“春” 张卡片,则额外获得2分.
张卡片,则额外获得2分.
(1)求学生甲抽到“福”“龙”“迎”“春”4张卡片的不同的抽法种数;
(2)求学生乙最终获得 分的不同的抽法种数.
分的不同的抽法种数.
 张卡片,则额外获得2分.
张卡片,则额外获得2分.(1)求学生甲抽到“福”“龙”“迎”“春”4张卡片的不同的抽法种数;
(2)求学生乙最终获得
 分的不同的抽法种数.
分的不同的抽法种数.
您最近一年使用:0次
2024-01-17更新
|
547次组卷
|
7卷引用:江西省上饶艺术学校2023-2024学年高二上学期期末数学试题
江西省上饶艺术学校2023-2024学年高二上学期期末数学试题上海市华东师范大学附属东昌中学2023-2024学年高二上学期期末考试数学试卷(已下线)专题16 组合7种常见考法归类-【寒假自学课】2024年高二数学寒假提升学与练(苏教版2019)上海市嘉定区第二中学2023-2024学年高二下学期3月月考数学试题(已下线)模块一专题1《排列与组合》单元检测篇A基础卷 (已下线)7.3组合 (3)(已下线)模块一 专题7《排列与组合》A基础卷(苏教版)
名校
9 . 2023年8月8日,为期12天的第31届世界大学生夏季运动会在成都圆满落幕.“天府之国”以一场青春盛宴,为来自世界113个国家和地区的6500名运动员留下了永恒的记忆.在这期间,成都大熊猫繁育研究基地成为各参赛代表团的热门参观地,大熊猫玩偶成为了颇受欢迎的纪念品.某大熊猫玩偶生产公司设计了某款新产品,为生产该产品需要引进新型设备.已知购买该新型设备需要5万元,之后每生产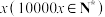 万件产品,还需另外投入原料费及其他费用
万件产品,还需另外投入原料费及其他费用 万元,且
万元,且 ,已知每件产品的售价为20元且生产的该产品可以全部卖出.
,已知每件产品的售价为20元且生产的该产品可以全部卖出.
(1)写出利润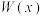 (万元)关于产量
(万元)关于产量 (万件)的函数解析式.
(万件)的函数解析式.
(2)该产品产量为多少万件时,公司所获的利润最大?其最大利润为多少万元?
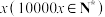 万件产品,还需另外投入原料费及其他费用
万件产品,还需另外投入原料费及其他费用 万元,且
万元,且 ,已知每件产品的售价为20元且生产的该产品可以全部卖出.
,已知每件产品的售价为20元且生产的该产品可以全部卖出.(1)写出利润
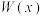 (万元)关于产量
(万元)关于产量 (万件)的函数解析式.
(万件)的函数解析式.(2)该产品产量为多少万件时,公司所获的利润最大?其最大利润为多少万元?
您最近一年使用:0次
2024-01-13更新
|
366次组卷
|
3卷引用:江西省宜春市丰城市东煌学校2024届高三上学期期末数学试题
名校
解题方法
10 . 瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上,这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中, 满足
满足 ,顶点
,顶点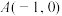 、
、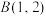 ,且其“欧拉线”与圆
,且其“欧拉线”与圆 相切.
相切.
(1)求 的“欧拉线”方程;
的“欧拉线”方程;
(2)若圆M与圆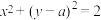 有公共点,求a的范围;
有公共点,求a的范围;
(3)若点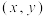 在
在 的“欧拉线”上,求
的“欧拉线”上,求 的最小值.
的最小值.
 满足
满足 ,顶点
,顶点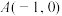 、
、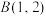 ,且其“欧拉线”与圆
,且其“欧拉线”与圆 相切.
相切.(1)求
 的“欧拉线”方程;
的“欧拉线”方程;(2)若圆M与圆
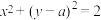 有公共点,求a的范围;
有公共点,求a的范围;(3)若点
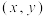 在
在 的“欧拉线”上,求
的“欧拉线”上,求 的最小值.
的最小值.
您最近一年使用:0次
2023-11-16更新
|
416次组卷
|
4卷引用:江西省2023-2024学年高二上学期期末教学检测数学试题



