名校
1 . 已知数集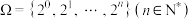 .若
.若 的两个非空子集
的两个非空子集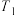 和
和 满足:
满足: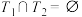 ,
,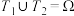 ,则称集合
,则称集合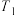 和
和 是
是 的一个“分拆”.已知
的一个“分拆”.已知 和
和 是
是 的一个分拆,
的一个分拆,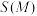 表示数集
表示数集 中所有元素的和.
中所有元素的和.
(1)若 ,
,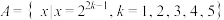 ,求
,求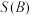 ;(用数值表示)
;(用数值表示)
(2)证明: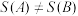 ;
;
(3)若n为给定的偶数,关于 的方程
的方程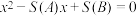 有整数根,求
有整数根,求 的最小值,并写出取到最小值时的所有的集合A.
的最小值,并写出取到最小值时的所有的集合A.
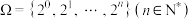 .若
.若 的两个非空子集
的两个非空子集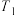 和
和 满足:
满足: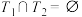 ,
,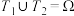 ,则称集合
,则称集合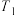 和
和 是
是 的一个“分拆”.已知
的一个“分拆”.已知 和
和 是
是 的一个分拆,
的一个分拆,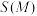 表示数集
表示数集 中所有元素的和.
中所有元素的和.(1)若
 ,
,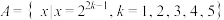 ,求
,求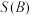 ;(用数值表示)
;(用数值表示)(2)证明:
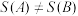 ;
;(3)若n为给定的偶数,关于
 的方程
的方程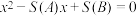 有整数根,求
有整数根,求 的最小值,并写出取到最小值时的所有的集合A.
的最小值,并写出取到最小值时的所有的集合A.
您最近一年使用:0次
名校
解题方法
2 . 小郅同学的左、右口袋中分别装有3个糖果,每次取糖他都有 的概率从右口袋中取,每次取糖过程相互独立.当他发现某个口袋中没有糖时停止取糖.
的概率从右口袋中取,每次取糖过程相互独立.当他发现某个口袋中没有糖时停止取糖.
(1)求当他右口袋为空时,左口袋中剩余2个糖的概率 ,并求出
,并求出 的值使
的值使 最大.
最大.
(2)若 ,求小郅最终发现其右口袋没有糖的概率.
,求小郅最终发现其右口袋没有糖的概率.
(3)对于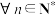 ,求证成立不等式:
,求证成立不等式: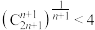 .
.
 的概率从右口袋中取,每次取糖过程相互独立.当他发现某个口袋中没有糖时停止取糖.
的概率从右口袋中取,每次取糖过程相互独立.当他发现某个口袋中没有糖时停止取糖.(1)求当他右口袋为空时,左口袋中剩余2个糖的概率
 ,并求出
,并求出 的值使
的值使 最大.
最大.(2)若
 ,求小郅最终发现其右口袋没有糖的概率.
,求小郅最终发现其右口袋没有糖的概率.(3)对于
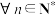 ,求证成立不等式:
,求证成立不等式: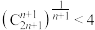 .
.
您最近一年使用:0次
2024-10-22更新
|
275次组卷
|
4卷引用:江西省新余市第四中学2024届高三下学期5月高考全真模拟(三)数学试题
江西省新余市第四中学2024届高三下学期5月高考全真模拟(三)数学试题(已下线)第06讲 事件的相互独立性、条件概率与全概率公式(七大题型)(练习)广西钦州市第四中学2025届高三上学期9月份考试数学试题(已下线)重难点突破02 概率、统计与其他知识的交汇问题(五大题型)
名校
解题方法
3 . 已知函数 的定义域和值域分别为
的定义域和值域分别为 ,若函数
,若函数 满足:(i)
满足:(i) 的定义域为
的定义域为 ;(ii)
;(ii) 的值域为
的值域为 ;(iii)
;(iii)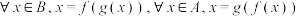 ,则称
,则称 与
与 具有
具有 关系.
关系.
(1)若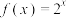 ,判断下列两个函数是否与
,判断下列两个函数是否与 具有
具有 关系,并说明理由;
关系,并说明理由;
①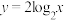 ;②
;②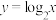 .
.
(2)若 与
与 具有
具有 关系,证明:函数
关系,证明:函数 的图象与
的图象与 的图象关于直线
的图象关于直线 对称;
对称;
(3)已知函数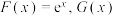 与
与 具有
具有 关系,令
关系,令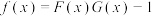 .
.
①判断函数 的单调性;
的单调性;
②证明: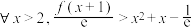 .
.
 的定义域和值域分别为
的定义域和值域分别为 ,若函数
,若函数 满足:(i)
满足:(i) 的定义域为
的定义域为 ;(ii)
;(ii) 的值域为
的值域为 ;(iii)
;(iii)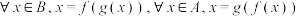 ,则称
,则称 与
与 具有
具有 关系.
关系.(1)若
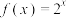 ,判断下列两个函数是否与
,判断下列两个函数是否与 具有
具有 关系,并说明理由;
关系,并说明理由;①
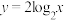 ;②
;②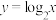 .
.(2)若
 与
与 具有
具有 关系,证明:函数
关系,证明:函数 的图象与
的图象与 的图象关于直线
的图象关于直线 对称;
对称;(3)已知函数
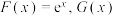 与
与 具有
具有 关系,令
关系,令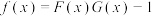 .
.①判断函数
 的单调性;
的单调性;②证明:
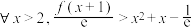 .
.
您最近一年使用:0次
名校
解题方法
4 . 如图(1),已知抛物线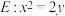 的焦点为
的焦点为 ,准线为
,准线为 ,过点
,过点 的动直线
的动直线 与
与 交于A,B两点(其中点A在第一象限),以AB为直径的圆与准线
交于A,B两点(其中点A在第一象限),以AB为直径的圆与准线 相切于点C,D为弦AB上任意一点,现将
相切于点C,D为弦AB上任意一点,现将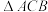 沿CD折成直二面角
沿CD折成直二面角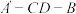 ,如图(2).
,如图(2).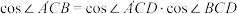 ;
;
(2)当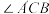 最小时,
最小时,
①求 ,
, 两点间的最小距离;
两点间的最小距离;
②当 ,
, 两点间的距离最小时,在三棱锥
两点间的距离最小时,在三棱锥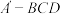 内部放一圆柱,使圆柱底面在面BCD上,求圆柱体积的最大值.
内部放一圆柱,使圆柱底面在面BCD上,求圆柱体积的最大值.
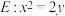 的焦点为
的焦点为 ,准线为
,准线为 ,过点
,过点 的动直线
的动直线 与
与 交于A,B两点(其中点A在第一象限),以AB为直径的圆与准线
交于A,B两点(其中点A在第一象限),以AB为直径的圆与准线 相切于点C,D为弦AB上任意一点,现将
相切于点C,D为弦AB上任意一点,现将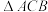 沿CD折成直二面角
沿CD折成直二面角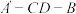 ,如图(2).
,如图(2).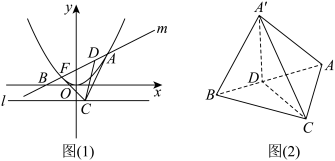
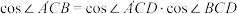 ;
;(2)当
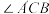 最小时,
最小时,①求
 ,
, 两点间的最小距离;
两点间的最小距离;②当
 ,
, 两点间的距离最小时,在三棱锥
两点间的距离最小时,在三棱锥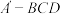 内部放一圆柱,使圆柱底面在面BCD上,求圆柱体积的最大值.
内部放一圆柱,使圆柱底面在面BCD上,求圆柱体积的最大值.
您最近一年使用:0次
5 . 在平面直角坐标系 中,等轴双曲线
中,等轴双曲线 和
和 的中心均为O,焦点分别在x轴和y轴上,焦距之比为2,
的中心均为O,焦点分别在x轴和y轴上,焦距之比为2, 的右焦点F到
的右焦点F到 的渐近线的距离为2.
的渐近线的距离为2.
(1)求 ,
, 的方程;
的方程;
(2)过F的直线交 于A,B两点,交
于A,B两点,交 于D,E两点,
于D,E两点, 与
与 的方向相同.
的方向相同.
(ⅰ)证明: ;
;
(ⅱ)求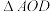 面积的最小值.
面积的最小值.
 中,等轴双曲线
中,等轴双曲线 和
和 的中心均为O,焦点分别在x轴和y轴上,焦距之比为2,
的中心均为O,焦点分别在x轴和y轴上,焦距之比为2, 的右焦点F到
的右焦点F到 的渐近线的距离为2.
的渐近线的距离为2.(1)求
 ,
, 的方程;
的方程;(2)过F的直线交
 于A,B两点,交
于A,B两点,交 于D,E两点,
于D,E两点, 与
与 的方向相同.
的方向相同.(ⅰ)证明:
 ;
;(ⅱ)求
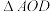 面积的最小值.
面积的最小值.
您最近一年使用:0次
名校
解题方法
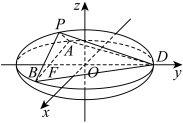
6 . 如图:在空间直角坐标系中有椭圆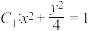 与
与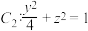 正交,
正交, 为
为 的右顶点,
的右顶点, 为
为 上一点,平面
上一点,平面 内的直线
内的直线 经过
经过 并与
并与 交于
交于 两点,在平面直角坐标系
两点,在平面直角坐标系 与
与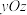 中(规定垂直于平面系观察时
中(规定垂直于平面系观察时 轴、
轴、 轴分别为对应平面系的纵轴,正方向竖直向上,横轴正方向水平向右),不与坐标轴平行的直线
轴分别为对应平面系的纵轴,正方向竖直向上,横轴正方向水平向右),不与坐标轴平行的直线 与
与 的斜率分别为
的斜率分别为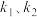 .
.
(1)若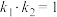 ,当三棱锥
,当三棱锥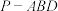 体积取最大值时,求
体积取最大值时,求 ;
;
(2)探究:是否存在定点 使平面
使平面
 平面
平面 不论
不论 取何值恒成立?若存在,求
取何值恒成立?若存在,求 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
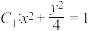 与
与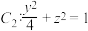 正交,
正交, 为
为 的右顶点,
的右顶点, 为
为 上一点,平面
上一点,平面 内的直线
内的直线 经过
经过 并与
并与 交于
交于 两点,在平面直角坐标系
两点,在平面直角坐标系 与
与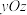 中(规定垂直于平面系观察时
中(规定垂直于平面系观察时 轴、
轴、 轴分别为对应平面系的纵轴,正方向竖直向上,横轴正方向水平向右),不与坐标轴平行的直线
轴分别为对应平面系的纵轴,正方向竖直向上,横轴正方向水平向右),不与坐标轴平行的直线 与
与 的斜率分别为
的斜率分别为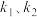 .
.
(1)若
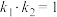 ,当三棱锥
,当三棱锥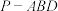 体积取最大值时,求
体积取最大值时,求 ;
;(2)探究:是否存在定点
 使平面
使平面
 平面
平面 不论
不论 取何值恒成立?若存在,求
取何值恒成立?若存在,求 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近一年使用:0次
7 . 设计一个帐篷,它下部的形状是正四棱柱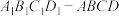 ,上部的形状是正四棱锥
,上部的形状是正四棱锥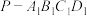 ,且该帐篷外接于球
,且该帐篷外接于球 (如图所示).
(如图所示).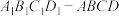 是棱长为
是棱长为 的正方体,求该帐篷的顶点
的正方体,求该帐篷的顶点 到底面
到底面 中心
中心 的距离;
的距离;
(2)若该帐篷外接球 的半径
的半径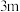 ,设
,设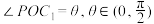 ,该帐篷的体积为
,该帐篷的体积为 ,则当
,则当 为何值时,体积
为何值时,体积 取得最大值.
取得最大值.
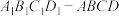 ,上部的形状是正四棱锥
,上部的形状是正四棱锥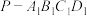 ,且该帐篷外接于球
,且该帐篷外接于球 (如图所示).
(如图所示).
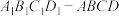 是棱长为
是棱长为 的正方体,求该帐篷的顶点
的正方体,求该帐篷的顶点 到底面
到底面 中心
中心 的距离;
的距离;(2)若该帐篷外接球
 的半径
的半径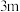 ,设
,设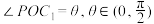 ,该帐篷的体积为
,该帐篷的体积为 ,则当
,则当 为何值时,体积
为何值时,体积 取得最大值.
取得最大值.
您最近一年使用:0次
2024-09-23更新
|
227次组卷
|
3卷引用:江苏省淮安市十校2024-2025学年高三上学期第一次联考数学试题
解题方法
8 . 开区间上的连续函数有最值吗?
您最近一年使用:0次
解题方法
9 . 记函数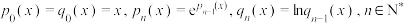 .
.
(1)证明: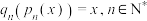 ;
;
(2)记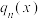 的定义域为
的定义域为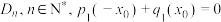 .若任意
.若任意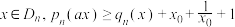 ,求
,求 的取值范围.
的取值范围.
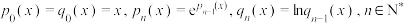 .
.(1)证明:
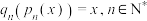 ;
;(2)记
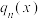 的定义域为
的定义域为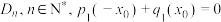 .若任意
.若任意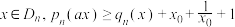 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
10 . 在平面直角坐标系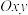 中,定义:如果曲线
中,定义:如果曲线 和
和 上分别存在点
上分别存在点 ,
, 关于
关于 轴对称,则称点
轴对称,则称点 和点
和点 为
为 和
和 的一对“关联点”.
的一对“关联点”.
(1)若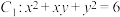 上任意一点
上任意一点 的“关联点”为点
的“关联点”为点 ,求点
,求点 所在的曲线方程和
所在的曲线方程和 的最小值;
的最小值;
(2)若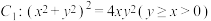 上任意一点
上任意一点 的“关联点”为点
的“关联点”为点 ,求
,求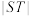 的最大值;
的最大值;
(3)若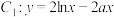 和
和 在区间
在区间 上有且仅有两对“关联点”,求实数
上有且仅有两对“关联点”,求实数 的取值范围.
的取值范围.
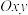 中,定义:如果曲线
中,定义:如果曲线 和
和 上分别存在点
上分别存在点 ,
, 关于
关于 轴对称,则称点
轴对称,则称点 和点
和点 为
为 和
和 的一对“关联点”.
的一对“关联点”.(1)若
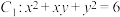 上任意一点
上任意一点 的“关联点”为点
的“关联点”为点 ,求点
,求点 所在的曲线方程和
所在的曲线方程和 的最小值;
的最小值;(2)若
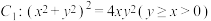 上任意一点
上任意一点 的“关联点”为点
的“关联点”为点 ,求
,求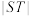 的最大值;
的最大值;(3)若
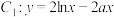 和
和 在区间
在区间 上有且仅有两对“关联点”,求实数
上有且仅有两对“关联点”,求实数 的取值范围.
的取值范围.
您最近一年使用:0次



