名校
解题方法
1 . 单位面积穗数、穗粒数、千粒重是影响小麦产量的主要因素,某小麦品种培育基地在一块试验田种植了一个小麦新品种,收获时随机选取了100个小麦穗,对每个小麦穗上的小麦粒数进行统计得到如下统计表:
其中同一组中的数据用该组区间的中点值作代表.从收获的小麦粒中随机选取5组,每组1000粒,分别称重,得到这5组的质量(单位: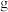 )分别为:
)分别为: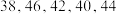 .
.
(1)根据抽测,这块试验田的小麦亩穗数为40万,试估计这块试验田的小麦亩产量(结果四舍五入到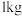 );
);
公式:亩产量 亩穗数
亩穗数 样本平均穗粒数
样本平均穗粒数 .
.
(2)已知该试验田穗粒数 近似服从正态分布
近似服从正态分布 ,其中
,其中 近似为样本平均数,
近似为样本平均数, 近似为样本方差.若小麦穗粒数不低于28粒的穗数超过总体的
近似为样本方差.若小麦穗粒数不低于28粒的穗数超过总体的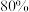 ,则称该小麦品种为优质小麦品种,试判断该试验田中的小麦品种是否为优质小麦品种.
,则称该小麦品种为优质小麦品种,试判断该试验田中的小麦品种是否为优质小麦品种.
参考数据:若 近似服从正态分布
近似服从正态分布 ,则
,则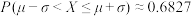 .
.
| 穗粒数 | 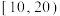 | 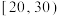 | 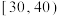 |  |  |
| 穗数 | 4 | 10 | 56 | 22 | 8 |
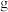 )分别为:
)分别为: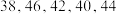 .
.(1)根据抽测,这块试验田的小麦亩穗数为40万,试估计这块试验田的小麦亩产量(结果四舍五入到
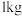 );
);公式:亩产量
 亩穗数
亩穗数 样本平均穗粒数
样本平均穗粒数 .
.(2)已知该试验田穗粒数
 近似服从正态分布
近似服从正态分布 ,其中
,其中 近似为样本平均数,
近似为样本平均数, 近似为样本方差.若小麦穗粒数不低于28粒的穗数超过总体的
近似为样本方差.若小麦穗粒数不低于28粒的穗数超过总体的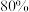 ,则称该小麦品种为优质小麦品种,试判断该试验田中的小麦品种是否为优质小麦品种.
,则称该小麦品种为优质小麦品种,试判断该试验田中的小麦品种是否为优质小麦品种.参考数据:若
 近似服从正态分布
近似服从正态分布 ,则
,则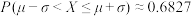 .
.
您最近一年使用:0次
名校
解题方法
2 . 某兴趣小组调查并统计了某班级学生期末统考中的数学成绩和建立个性化错题本的情况,用来研究这两者是否有关.若从该班级中随机抽取1名学生,设 “抽取的学生期末统考中的数学成绩不及格”,
“抽取的学生期末统考中的数学成绩不及格”, “抽取的学生建立了个性化错题本”,且
“抽取的学生建立了个性化错题本”,且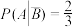 ,
,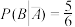 ,
, .
.
(1)求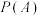 和
和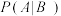 .
.
(2)若该班级共有36名学生,请完成列联表,并依据小概率值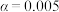 的独立性检验,分析学生期末统考中的数学成绩与建立个性化错题本是否有关,
的独立性检验,分析学生期末统考中的数学成绩与建立个性化错题本是否有关,
(3)为进一步验证(2)中的判断,该兴趣小组准备在其他班级中抽取一个容量为 的样本(假设根据新样本数据建立的列联表中,所有的数据都扩大为(2)中列联表中数据的
的样本(假设根据新样本数据建立的列联表中,所有的数据都扩大为(2)中列联表中数据的 倍,且新列联表中的数据都为整数).若要使得依据
倍,且新列联表中的数据都为整数).若要使得依据 的独立性检验可以肯定(2)中的判断,试确定
的独立性检验可以肯定(2)中的判断,试确定 的最小值
的最小值
参考公式及数据: ,
, .
.
 “抽取的学生期末统考中的数学成绩不及格”,
“抽取的学生期末统考中的数学成绩不及格”, “抽取的学生建立了个性化错题本”,且
“抽取的学生建立了个性化错题本”,且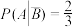 ,
,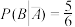 ,
, .
.(1)求
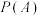 和
和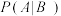 .
.(2)若该班级共有36名学生,请完成列联表,并依据小概率值
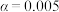 的独立性检验,分析学生期末统考中的数学成绩与建立个性化错题本是否有关,
的独立性检验,分析学生期末统考中的数学成绩与建立个性化错题本是否有关,个性化错题本 | 期末统考中的数学成绩 | 合计 | |
及格 | 不及格 | ||
建立 | |||
未建立 | |||
合计 | |||
 的样本(假设根据新样本数据建立的列联表中,所有的数据都扩大为(2)中列联表中数据的
的样本(假设根据新样本数据建立的列联表中,所有的数据都扩大为(2)中列联表中数据的 倍,且新列联表中的数据都为整数).若要使得依据
倍,且新列联表中的数据都为整数).若要使得依据 的独立性检验可以肯定(2)中的判断,试确定
的独立性检验可以肯定(2)中的判断,试确定 的最小值
的最小值参考公式及数据:
 ,
, .
.
| 0.01 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-05-08更新
|
1701次组卷
|
6卷引用:河北省保定市九校2024届高三下学期二模数学试题
名校
解题方法
3 . 有4个外包装相同的盒子,其中2个盒子分别装有1个白球,另外2个盒子分别装有1个黑球,现准备将每个盒子逐个拆开,则恰好拆开2个盒子就能确定2个白球在哪个盒子中的概率为( )
A. | B. | C. | D. |
您最近一年使用:0次
2024-05-08更新
|
2341次组卷
|
10卷引用:河北省保定市九校2024届高三下学期二模数学试题
河北省保定市九校2024届高三下学期二模数学试题山西省晋城市2024届高三第三次模拟考试数学试题(已下线)江苏省苏锡常镇四市2024届高三下学期教学情况调研考试数学试题浙江省强基联盟2024届高三下学期5月全国“优创名校”联考数学试题(已下线)第五套 艺体生新高考全真模拟 (二模重组卷)辽宁省抚顺市六校协作体2024届高三下学期5月模拟考试数学试卷山东省日照市五莲县第一中学2024届高三第三次模拟考试数学试题广西钦州市2024届高三年级第三次教学质量监测 数学山东省菏泽市鄄城县2023-2024学年高二下学期5月月考数学试题湖南省株洲市炎陵县2023-2024学年高二下学期6月期末考试数学试题
名校
4 . 甲企业生产线上生产的零件尺寸的误差 服从正态分布
服从正态分布 ,规定
,规定 的零件为优等品,
的零件为优等品, 的零件为合格品.
的零件为合格品.
(1)从该生产线上随机抽取100个零件,估计抽到合格品但非优等品的个数(精确到整数);
(2)乙企业拟向甲企业购买这批零件,先对该批零件进行质量抽检,检测的方案是:从这批零件中任取2个作检测,若这2个零件都是优等品,则通过检测;若这2个零件中恰有1个为优等品,1个为合格品但非优等品,则再从这批零件中任取1个作检测,若为优等品,则通过检测;其余情况都不通过检测.求这批零件通过检测时,检测了2个零件的概率(精确到0.01).
(附:若随机变量 ,则
,则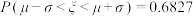 ,
,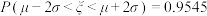 ,
,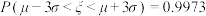 )
)
 服从正态分布
服从正态分布 ,规定
,规定 的零件为优等品,
的零件为优等品, 的零件为合格品.
的零件为合格品.(1)从该生产线上随机抽取100个零件,估计抽到合格品但非优等品的个数(精确到整数);
(2)乙企业拟向甲企业购买这批零件,先对该批零件进行质量抽检,检测的方案是:从这批零件中任取2个作检测,若这2个零件都是优等品,则通过检测;若这2个零件中恰有1个为优等品,1个为合格品但非优等品,则再从这批零件中任取1个作检测,若为优等品,则通过检测;其余情况都不通过检测.求这批零件通过检测时,检测了2个零件的概率(精确到0.01).
(附:若随机变量
 ,则
,则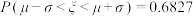 ,
,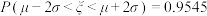 ,
,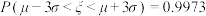 )
)
您最近一年使用:0次
2024-05-07更新
|
1386次组卷
|
5卷引用:专题2 科学研究情境
(已下线)专题2 科学研究情境河北省邢台市南宫中学2023-2024学年高三高考考前定心卷3数学试题(已下线)二项分布与超几何分布、正态分布-一轮复习考点专练(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(练习)-1福建省福州市2023-2024学年高三下学期4月末质量检测数学试卷
名校
5 . 在科技飞速发展的今天,人工智能领域迎来革命性的突破.类似于OpenAI的人工智能大模型不仅具有高度智能化、自主化和自适应的特点,它们的学习能力和信息储存能力也远远超越人类,更是拥有强大的语音识别和语言理解能力.某机构分别用 ,
, 两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中
两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中 人工智能大模型回答100个问题,有90个正确;
人工智能大模型回答100个问题,有90个正确; 人工智能大模型回答剩下的80个问题,有65个正确.
人工智能大模型回答剩下的80个问题,有65个正确.
(1)完成下列 列联表,并根据小概率值
列联表,并根据小概率值 的
的 独立性检验,能否判断人工智能大模型的选择和回答正确有关?
独立性检验,能否判断人工智能大模型的选择和回答正确有关?
(2)将频率视为概率,用 人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为
人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考公式及参考数据: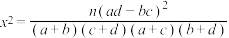 ,
, .
.
 ,
, 两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中
两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中 人工智能大模型回答100个问题,有90个正确;
人工智能大模型回答100个问题,有90个正确; 人工智能大模型回答剩下的80个问题,有65个正确.
人工智能大模型回答剩下的80个问题,有65个正确.(1)完成下列
 列联表,并根据小概率值
列联表,并根据小概率值 的
的 独立性检验,能否判断人工智能大模型的选择和回答正确有关?
独立性检验,能否判断人工智能大模型的选择和回答正确有关?| 回答正确 | 回答错误 | 合计 | |
 人工智能大模型 人工智能大模型 | |||
 人工智能大模型 人工智能大模型 | |||
| 合计 |
 人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为
人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.参考公式及参考数据:
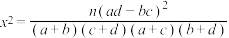 ,
, .
.
| 0.15 | 0.10 | 0.05 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2024-05-03更新
|
976次组卷
|
6卷引用:情境2 最新科技前沿
(已下线)情境2 最新科技前沿(已下线)高二期末模拟卷02(已下线)专题04 第八章 成对数据的统计分析--高二期末考点大串讲(人教A版2019)河北省邢台市南宫中学2023-2024学年高三高考考前定心卷2数学试题贵州省凯里市第一中学2024届高三模拟考试(二模)数学试题湖北省宜昌市远安县第一高级中学2023-2024学年高二下学期5月月考数学试卷
名校
解题方法
6 . 已知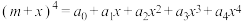 ,
,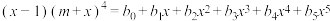 ,其中
,其中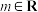 ,
,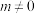 .若
.若 ,则( )
,则( )
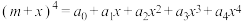 ,
,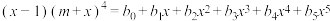 ,其中
,其中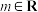 ,
,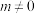 .若
.若 ,则( )
,则( )A. | B.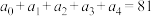 |
C.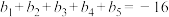 | D. |
您最近一年使用:0次
2024-04-30更新
|
965次组卷
|
4卷引用:河北省部分高中2024届高三下学期二模考试数学试题
河北省部分高中2024届高三下学期二模考试数学试题(已下线)2024年普通高等学校招生全国统一考试数学押题卷(一)河南省郑州市宇华实验学校2024届高三下学期5月月考数学试题福建省福州市福建师范大学附属中学2025届高三上学期第一次月考(10月)数学试题
名校
解题方法
7 . 已知随机变量 服从正态分布
服从正态分布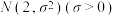 ,则“
,则“ ”是“
”是“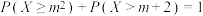 ”的( )
”的( )
 服从正态分布
服从正态分布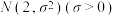 ,则“
,则“ ”是“
”是“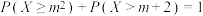 ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
2024-04-30更新
|
1723次组卷
|
6卷引用:河北省部分高中2024届高三下学期二模考试数学试题
河北省部分高中2024届高三下学期二模考试数学试题(已下线)8.5 二项分布、超几何分布与正态分布(高考真题素材之十年高考)(已下线)2024年普通高等学校招生全国统一考试数学押题卷(一)江苏省苏州实验中学2023-2024学年高二下学期5月月考数学试题浙江省嘉兴高级中学2023-2024学年高二下学期期中考试数学试卷福建省福州市福建师范大学附属中学2025届高三上学期第一次月考(10月)数学试题
8 . 现有13个数学竞赛参赛名额分给五个班,其中一班和二班每班至少3个名额,三班和四班每班至少2个名额,五班可以不分配名额,则名额分配方式共有( ).
| A.15种 | B.35种 | C.70种 | D.125种 |
您最近一年使用:0次
2024高三下·全国·专题练习
名校
解题方法
9 . “九子游戏”是一种传统的儿童游戏,它包括打弹子、滚圈子、踢毽子、顶核子、造房子、拉扯铃子、刮片子、掼结子、抽陀子九种不同的游戏项目,某小学为丰富同学们的课外活动,举办了“九子游戏”比赛,所有的比赛项目均采用 局
局 胜的单败淘汰制,即先赢下
胜的单败淘汰制,即先赢下 局比赛者获胜.造房子游戏是同学们喜爱的项目之一,经过多轮淘汰后,甲、乙二人进入造房子游戏的决赛,已知每局比赛甲获胜的概率为
局比赛者获胜.造房子游戏是同学们喜爱的项目之一,经过多轮淘汰后,甲、乙二人进入造房子游戏的决赛,已知每局比赛甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 .
.
(1)若 ,
, ,设比赛结束时比赛的局数为
,设比赛结束时比赛的局数为 ,求
,求 的分布列与数学期望;
的分布列与数学期望;
(2)设采用3局2胜制时乙获胜的概率为 ,采用5局3胜制时乙获胜的概率为
,采用5局3胜制时乙获胜的概率为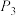 ,若
,若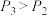 ,求
,求 的取值范围.
的取值范围.
 局
局 胜的单败淘汰制,即先赢下
胜的单败淘汰制,即先赢下 局比赛者获胜.造房子游戏是同学们喜爱的项目之一,经过多轮淘汰后,甲、乙二人进入造房子游戏的决赛,已知每局比赛甲获胜的概率为
局比赛者获胜.造房子游戏是同学们喜爱的项目之一,经过多轮淘汰后,甲、乙二人进入造房子游戏的决赛,已知每局比赛甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 .
.(1)若
 ,
, ,设比赛结束时比赛的局数为
,设比赛结束时比赛的局数为 ,求
,求 的分布列与数学期望;
的分布列与数学期望;(2)设采用3局2胜制时乙获胜的概率为
 ,采用5局3胜制时乙获胜的概率为
,采用5局3胜制时乙获胜的概率为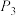 ,若
,若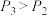 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-04-26更新
|
2124次组卷
|
6卷引用:2024年普通高等学校招生全国统一考试数学理科押题卷(四)
(已下线)2024年普通高等学校招生全国统一考试数学理科押题卷(四)河北省部分高中2024届高三下学期二模考试数学试题(已下线)情境3 落实五育并举(已下线)2024年普通高等学校招生全国统一考试数学押题卷(一)甘肃省民乐县第一中学2023-2024学年高三下学期5月第一次模拟考试数学试卷福建省福州市福建师范大学附属中学2025届高三上学期第一次月考(10月)数学试题
名校
10 . 2024年7月26日至8月11日将在法国巴黎举行夏季奥运会.为了普及奥运知识,M大学举办了一次奥运知识竞赛,竞赛分为初赛与决赛,初赛通过后才能参加决赛
(1)初赛从6道题中任选2题作答,2题均答对则进入决赛.已知这6道题中小王能答对其中4道题,记小王在初赛中答对的题目个数为 ,求
,求 的数学期望以及小王在已经答对一题的前提下,仍未进入决赛的概率;
的数学期望以及小王在已经答对一题的前提下,仍未进入决赛的概率;
(2) 大学为鼓励大学生踊跃参赛并取得佳绩,对进入决赛的参赛大学生给予一定的奖励.奖励规则如下:已进入决赛的参赛大学生允许连续抽奖3次,中奖1次奖励120元,中奖2次奖励180元,中奖3次奖励360元,若3次均未中奖,则只奖励60元.假定每次抽奖中奖的概率均为
大学为鼓励大学生踊跃参赛并取得佳绩,对进入决赛的参赛大学生给予一定的奖励.奖励规则如下:已进入决赛的参赛大学生允许连续抽奖3次,中奖1次奖励120元,中奖2次奖励180元,中奖3次奖励360元,若3次均未中奖,则只奖励60元.假定每次抽奖中奖的概率均为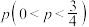 ,且每次是否中奖相互独立.
,且每次是否中奖相互独立.
(i)记一名进入决赛的大学生恰好中奖1次的概率为 ,求
,求 的极大值;
的极大值;
(ii) 大学数学系共有9名大学生进入了决赛,若这9名大学生获得的总奖金的期望值不小于1120元,试求此时
大学数学系共有9名大学生进入了决赛,若这9名大学生获得的总奖金的期望值不小于1120元,试求此时 的取值范围.
的取值范围.
(1)初赛从6道题中任选2题作答,2题均答对则进入决赛.已知这6道题中小王能答对其中4道题,记小王在初赛中答对的题目个数为
 ,求
,求 的数学期望以及小王在已经答对一题的前提下,仍未进入决赛的概率;
的数学期望以及小王在已经答对一题的前提下,仍未进入决赛的概率;(2)
 大学为鼓励大学生踊跃参赛并取得佳绩,对进入决赛的参赛大学生给予一定的奖励.奖励规则如下:已进入决赛的参赛大学生允许连续抽奖3次,中奖1次奖励120元,中奖2次奖励180元,中奖3次奖励360元,若3次均未中奖,则只奖励60元.假定每次抽奖中奖的概率均为
大学为鼓励大学生踊跃参赛并取得佳绩,对进入决赛的参赛大学生给予一定的奖励.奖励规则如下:已进入决赛的参赛大学生允许连续抽奖3次,中奖1次奖励120元,中奖2次奖励180元,中奖3次奖励360元,若3次均未中奖,则只奖励60元.假定每次抽奖中奖的概率均为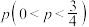 ,且每次是否中奖相互独立.
,且每次是否中奖相互独立.(i)记一名进入决赛的大学生恰好中奖1次的概率为
 ,求
,求 的极大值;
的极大值;(ii)
 大学数学系共有9名大学生进入了决赛,若这9名大学生获得的总奖金的期望值不小于1120元,试求此时
大学数学系共有9名大学生进入了决赛,若这9名大学生获得的总奖金的期望值不小于1120元,试求此时 的取值范围.
的取值范围.
您最近一年使用:0次
2024-04-24更新
|
2887次组卷
|
7卷引用:7.4 常见的几种分布列