名校
1 . 已知函数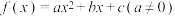 与
与 的图像都过点
的图像都过点 ,且在点
,且在点 处有公共切线.
处有公共切线.
(1)求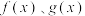 的表达式;
的表达式;
(2)过点 作曲线
作曲线 的切线,使切点
的切线,使切点 在第三象限,求点
在第三象限,求点 的坐标.
的坐标.
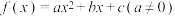 与
与 的图像都过点
的图像都过点 ,且在点
,且在点 处有公共切线.
处有公共切线.(1)求
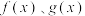 的表达式;
的表达式;(2)过点
 作曲线
作曲线 的切线,使切点
的切线,使切点 在第三象限,求点
在第三象限,求点 的坐标.
的坐标.
您最近一年使用:0次
2023-12-11更新
|
750次组卷
|
3卷引用:贵州省黔东南自治州镇远县文德民族中学校2021-2022学年高二上学期期末数学(文)试题
贵州省黔东南自治州镇远县文德民族中学校2021-2022学年高二上学期期末数学(文)试题江苏省南京市金陵中学2023-2024学年高二上学期1月期末数学试题(已下线)专题02 导数的运算(十大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)
2 . 已知曲线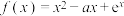 在
在 处的切线
处的切线 过点
过点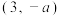 ,其中
,其中 ,则直线
,则直线 方程为( )
方程为( )
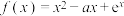 在
在 处的切线
处的切线 过点
过点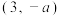 ,其中
,其中 ,则直线
,则直线 方程为( )
方程为( )A. | B.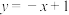 | C. | D. |
您最近一年使用:0次
名校
解题方法
3 . 已知椭圆 的右焦点为
的右焦点为 ,点
,点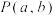 和
和 所连线段的中点在椭圆
所连线段的中点在椭圆 上,则椭圆的离心率为( )
上,则椭圆的离心率为( )
 的右焦点为
的右焦点为 ,点
,点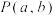 和
和 所连线段的中点在椭圆
所连线段的中点在椭圆 上,则椭圆的离心率为( )
上,则椭圆的离心率为( )A. | B.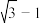 | C. | D.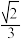 |
您最近一年使用:0次
2023-12-11更新
|
1588次组卷
|
8卷引用:贵州省黔东南自治州镇远县文德民族中学校2021-2022学年高二上学期期末数学(文)试题
贵州省黔东南自治州镇远县文德民族中学校2021-2022学年高二上学期期末数学(文)试题江西省上饶市广丰区南山中学2023-2024学年高二上学期期末模拟数学试题四川省成都市玉林中学2023-2024学年高二上学期期末模拟数学试题(一)(已下线)专题14 椭圆的离心率求算问题(期末选择题14)2023-2024学年高二数学上学期期末题型秒杀技巧及专项练习(人教A版2019)广东省广州市华南师范大学附属中学2022-2023学年高二上学期期末检测数学试题(已下线)模块一 专题4 圆锥曲线 期末终极研习室(2023-2024学年第一学期)高二人教A版陕西省渭南市高级中学2023-2024学年高二上学期12月月考数学试题(已下线)专题03 椭圆13种常见考法归类(3)
解题方法
4 . 已知函数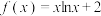 ,
,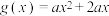 .
.
(1)当 时,求证:
时,求证: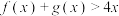 ;
;
(2)若 是函数
是函数 的导函数,且
的导函数,且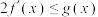 在定义域
在定义域 内恒成立,求整数a的最小值.
内恒成立,求整数a的最小值.
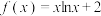 ,
,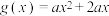 .
.(1)当
 时,求证:
时,求证: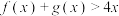 ;
;(2)若
 是函数
是函数 的导函数,且
的导函数,且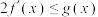 在定义域
在定义域 内恒成立,求整数a的最小值.
内恒成立,求整数a的最小值.
您最近一年使用:0次
名校
解题方法
5 . 如图,在四棱锥 中,底面ABCD是矩形,
中,底面ABCD是矩形, ,
, ,
, 底面ABCD,
底面ABCD, ,E为PB中点.
,E为PB中点.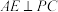 ;
;
(2)求平面EAD与平面PCD所成锐二面角的余弦值.
 中,底面ABCD是矩形,
中,底面ABCD是矩形, ,
, ,
, 底面ABCD,
底面ABCD, ,E为PB中点.
,E为PB中点.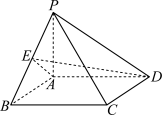
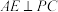 ;
;(2)求平面EAD与平面PCD所成锐二面角的余弦值.
您最近一年使用:0次
2023-12-11更新
|
1126次组卷
|
4卷引用:贵州省黔东南自治州镇远县文德民族中学校2022届高三上学期期末数学(理)试题
6 . 惠州市某工厂10名工人某天生产同一类型零件,生产的件数分别是10、12、14、14、15、15、16、17、17、17,记这组数据的平均数为 ,中位数为
,中位数为 ,众数为
,众数为 ,则( )
,则( )
 ,中位数为
,中位数为 ,众数为
,众数为 ,则( )
,则( )A.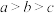 | B.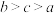 | C.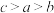 | D. |
您最近一年使用:0次
2023-12-11更新
|
1046次组卷
|
8卷引用:贵州省黔西南州兴义市顶效开发区顶兴学校2021-2022高二上学期期末考试数学(理)试题
贵州省黔西南州兴义市顶效开发区顶兴学校2021-2022高二上学期期末考试数学(理)试题(已下线)考点09 统计中各类数据 2024届高考数学考点总动员【讲】9.2.3总体集中趋势的估计练习2024年江苏省扬州市学业水平考试数学模拟试卷江苏省盐城市滨海县五汛中学2024届高三学业水平合格性调研考试(一)数学试题(已下线)9.2.3?总体集中趋势的估计——课堂例题(已下线)第05讲 9.2.3 总体集中趋势的估计-【帮课堂】(人教A版2019必修第二册)【导学案】4.1 样本的数字特征课前预习-北师大版2019必修第一册第六章统计
名校
解题方法
7 . 已知函数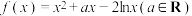
(1)当 时,求函数
时,求函数 的极值;
的极值;
(2)若函数 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
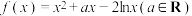
(1)当
 时,求函数
时,求函数 的极值;
的极值;(2)若函数
 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
您最近一年使用:0次
2023-12-11更新
|
4730次组卷
|
17卷引用:贵州省遵义市第二教育集团2021-2022学年高二上学期期末联考数学(文)试题
贵州省遵义市第二教育集团2021-2022学年高二上学期期末联考数学(文)试题江苏省南京市励志高级中学2023-2024学年高二上学期期末复习数学试题重庆市长寿区2024届高三上学期期末质量监测数学试题(B卷)陕西省西安市阎良区关山中学2024届高三上学期第一次质量检测数学(理)试题(已下线)专题04 函数的极值与最大(小)值 (十二大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)2024年普通高等学校招生全国统一考试数学模拟试题(一)(新高考九省联考题型)(已下线)专题10 利用导数研究函数的极值与最大(小)值 (十二大题型+过关检测专训)2024届河北省部分高中高考一模数学试题湖南省长沙市四县区2024届高三下学期3月调研考试数学试卷江苏省南通市海门中学2023-2024学年高二下学期3月学情调研数学试题广东省潮州市饶平县第二中学2023-2024学年高二下学期第一次月考数学试题(已下线)湖南省长沙市四县区2024届高三下学期3月调研考试数学试题变式题16-19江西省宜春市丰城中学2023-2024学年高二下学期4月期中考试数学试题江西省九江市武宁尚美中学2023-2024学年高二下学期5月月考数学试题云南省昆明市昆明师范专科学校附属中学2023-2024学年高二下学期5月期中学业质量监测数学试题江西省三新协作体2024届高三下学期5月联考数学模拟考试试题安徽省安庆市怀宁县第二中学2025届高三上学期第二次月考数学试卷
名校
8 . 已知函数 ,则
,则 在
在 处的切线与坐标轴围成的三角形的面积为
处的切线与坐标轴围成的三角形的面积为______ .
 ,则
,则 在
在 处的切线与坐标轴围成的三角形的面积为
处的切线与坐标轴围成的三角形的面积为
您最近一年使用:0次
2023-12-11更新
|
843次组卷
|
3卷引用:贵州省遵义市第二教育集团2021-2022学年高二上学期期末联考数学(文)试题
贵州省遵义市第二教育集团2021-2022学年高二上学期期末联考数学(文)试题福建省三明市第一中学2023-2024学年高二上学期12月月考数学试题(已下线)专题1.2 导数的运算(七个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
9 . 已知椭圆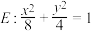
(1)椭圆 的左右顶点分别为
的左右顶点分别为 ,点
,点 为椭圆上异于
为椭圆上异于 的任意一点.证明:直线
的任意一点.证明:直线 与直线
与直线 的斜率乘积为定值;
的斜率乘积为定值;
(2)过点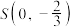 的动直线
的动直线 交椭圆
交椭圆 于
于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过这个点?若存在,求出点
为直径的圆恒过这个点?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
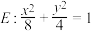
(1)椭圆
 的左右顶点分别为
的左右顶点分别为 ,点
,点 为椭圆上异于
为椭圆上异于 的任意一点.证明:直线
的任意一点.证明:直线 与直线
与直线 的斜率乘积为定值;
的斜率乘积为定值;(2)过点
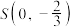 的动直线
的动直线 交椭圆
交椭圆 于
于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过这个点?若存在,求出点
为直径的圆恒过这个点?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
您最近一年使用:0次
解题方法
10 . 已知点 是抛物线
是抛物线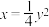 上的一个动点,则点
上的一个动点,则点 到点
到点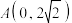 的距离与点
的距离与点 到
到 轴的距离之和的最小值为
轴的距离之和的最小值为______ .
 是抛物线
是抛物线 上的一个动点,则点
上的一个动点,则点 到点
到点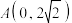 的距离与点
的距离与点 到
到 轴的距离之和的最小值为
轴的距离之和的最小值为
您最近一年使用:0次



