解题方法
1 . 已知函数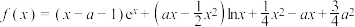 ,
, .
.
(1)讨论 的单调性;
的单调性;
(2)判断是否存在 ,使得
,使得 的最小值为
的最小值为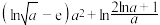 .若存在,确定符合条件的
.若存在,确定符合条件的 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
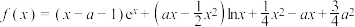 ,
, .
.(1)讨论
 的单调性;
的单调性;(2)判断是否存在
 ,使得
,使得 的最小值为
的最小值为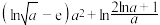 .若存在,确定符合条件的
.若存在,确定符合条件的 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
您最近一年使用:0次
2 . 一条直线与另外两条异面直线同时垂直且相交,则称该直线是两条异面直线的公垂线,并把以两垂足为端点的线段称为两异面直线的公垂线段,公垂线段的长度则被称为两异面直线之间的距离.
(1)用符号语言表述公垂线、公垂线段及两异面直线之间的距离的定义.
(2)证明:两条异面直线的公垂线有且仅有一条.
(3)在空间直角坐标系 中,直线
中,直线 过点
过点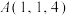 ,方向向量
,方向向量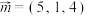 ;直线
;直线 过点
过点 ,方向向量
,方向向量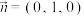 ,试问:
,试问: 与
与 是否共面?
是否共面?
Ⅰ.若共面,
(ⅰ)求 与
与 交点
交点 的坐标.
的坐标.
(ⅱ)已知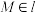 ,记
,记 与
与 所确定的平面为
所确定的平面为 ,记
,记 与
与 所确定的平面为
所确定的平面为 ,若
,若 ,试问:
,试问: 是否确定?若确定,求出
是否确定?若确定,求出 的单位方向向量;若不确定,请说明理由.
的单位方向向量;若不确定,请说明理由.
Ⅱ.若异面,
(ⅰ)请给出证明.
(ⅱ) 为
为 与
与 的公垂线,
的公垂线,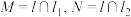 ,求
,求 与
与 之间的距离
之间的距离 .
.
(ⅲ)求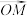 .
.
(1)用符号语言表述公垂线、公垂线段及两异面直线之间的距离的定义.
(2)证明:两条异面直线的公垂线有且仅有一条.
(3)在空间直角坐标系
 中,直线
中,直线 过点
过点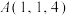 ,方向向量
,方向向量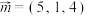 ;直线
;直线 过点
过点 ,方向向量
,方向向量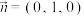 ,试问:
,试问: 与
与 是否共面?
是否共面?Ⅰ.若共面,
(ⅰ)求
 与
与 交点
交点 的坐标.
的坐标.(ⅱ)已知
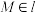 ,记
,记 与
与 所确定的平面为
所确定的平面为 ,记
,记 与
与 所确定的平面为
所确定的平面为 ,若
,若 ,试问:
,试问: 是否确定?若确定,求出
是否确定?若确定,求出 的单位方向向量;若不确定,请说明理由.
的单位方向向量;若不确定,请说明理由.Ⅱ.若异面,
(ⅰ)请给出证明.
(ⅱ)
 为
为 与
与 的公垂线,
的公垂线,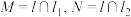 ,求
,求 与
与 之间的距离
之间的距离 .
.(ⅲ)求
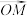 .
.
您最近一年使用:0次
名校
解题方法
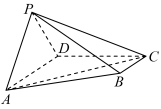
3 . 如图,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形,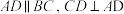 ,
,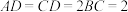 ,平面
,平面 平面
平面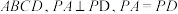 .
. ;
;
(2)求平面APB与平面 夹角的余弦值;
夹角的余弦值;
(3)在棱 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求
?若存在,求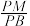 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 中,底面
中,底面 为直角梯形,
为直角梯形,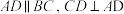 ,
,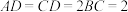 ,平面
,平面 平面
平面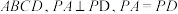 .
.
 ;
;(2)求平面APB与平面
 夹角的余弦值;
夹角的余弦值;(3)在棱
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求
?若存在,求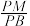 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
解题方法
4 . 如图,在四棱锥 中,底面ABCD是正方形,侧面PAD是等腰三角形,且
中,底面ABCD是正方形,侧面PAD是等腰三角形,且 ,侧面
,侧面 平面ABCD.
平面ABCD.
(2)设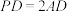 ,在线段PD上是否存在一点Q,使得
,在线段PD上是否存在一点Q,使得 ?若存在,求出
?若存在,求出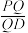 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,底面ABCD是正方形,侧面PAD是等腰三角形,且
中,底面ABCD是正方形,侧面PAD是等腰三角形,且 ,侧面
,侧面 平面ABCD.
平面ABCD.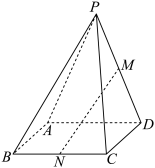
(2)设
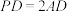 ,在线段PD上是否存在一点Q,使得
,在线段PD上是否存在一点Q,使得 ?若存在,求出
?若存在,求出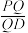 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
解题方法
5 . 已知 为等差数列,前
为等差数列,前 项和为
项和为 ,若
,若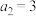 ,
, ;数列
;数列 满足:
满足: ,
, .
.
(1)求 和
和 的通项公式;
的通项公式;
(2)对任意的 ,将
,将 中落入区间
中落入区间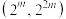 内项的个数记为
内项的个数记为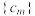 .
.
(i)求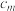 ;
;
(ii)记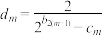 ,
,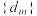 的前
的前 项和记为
项和记为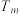 ,是否存在
,是否存在 ,
,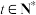 ,使得
,使得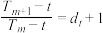 成立?若存在,求出
成立?若存在,求出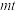 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 为等差数列,前
为等差数列,前 项和为
项和为 ,若
,若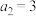 ,
, ;数列
;数列 满足:
满足: ,
, .
.(1)求
 和
和 的通项公式;
的通项公式;(2)对任意的
 ,将
,将 中落入区间
中落入区间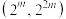 内项的个数记为
内项的个数记为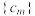 .
.(i)求
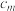 ;
;(ii)记
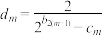 ,
,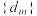 的前
的前 项和记为
项和记为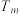 ,是否存在
,是否存在 ,
,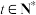 ,使得
,使得 成立?若存在,求出
成立?若存在,求出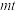 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
6 . 祖暅是我国南北朝时期杰出的数学家和天文学家祖冲之的儿子,他提出了一条原理:“幂势既同,则积不容异”,这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.利用祖暅原理可以将半球的体积转化为与其同底等高的圆柱和圆锥的体积之差.如图1是一种“四脚帐篷”的示意图,其中曲线AOC和BOD均是以 为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD,用任意平行于账篷底面ABCD的平面截帐篷,所得截面四边形均为正方形.模仿上述半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为( )
为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD,用任意平行于账篷底面ABCD的平面截帐篷,所得截面四边形均为正方形.模仿上述半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为( )
 为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD,用任意平行于账篷底面ABCD的平面截帐篷,所得截面四边形均为正方形.模仿上述半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为( )
为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD,用任意平行于账篷底面ABCD的平面截帐篷,所得截面四边形均为正方形.模仿上述半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为( )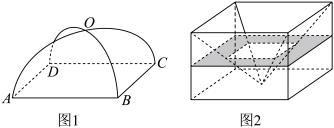
A.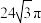 | B.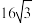 | C.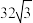 | D.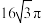 |
您最近一年使用:0次
7 . 正项数列 满足:对于
满足:对于 ,其中
,其中 为非零常数,则称数列
为非零常数,则称数列 为平方等差数列.记
为平方等差数列.记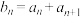 .
.
(1)判断无穷数列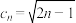 和
和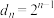 是否是平方等差数列,若是求出
是否是平方等差数列,若是求出 ,若不是,说明理由;
,若不是,说明理由;
(2)若 是平方等差数列且
是平方等差数列且 ,证明:任意的正常数
,证明:任意的正常数 ,存在正整数
,存在正整数 ,使得
,使得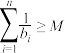 ;
;
(3)若 是平方等差数列,
是平方等差数列, ,令
,令 是不大于
是不大于 的最大整数,求
的最大整数,求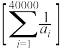 .
.
 满足:对于
满足:对于 ,其中
,其中 为非零常数,则称数列
为非零常数,则称数列 为平方等差数列.记
为平方等差数列.记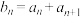 .
.(1)判断无穷数列
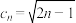 和
和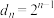 是否是平方等差数列,若是求出
是否是平方等差数列,若是求出 ,若不是,说明理由;
,若不是,说明理由;(2)若
 是平方等差数列且
是平方等差数列且 ,证明:任意的正常数
,证明:任意的正常数 ,存在正整数
,存在正整数 ,使得
,使得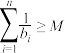 ;
;(3)若
 是平方等差数列,
是平方等差数列, ,令
,令 是不大于
是不大于 的最大整数,求
的最大整数,求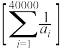 .
.
您最近一年使用:0次
名校
解题方法
8 . 某企业的设备控制系统由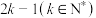 个相同的元件组成,每个元件正常工作的概率均为
个相同的元件组成,每个元件正常工作的概率均为 ,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为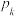 (例如:
(例如: 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).
(1)若 ,且每个元件正常工作的概率
,且每个元件正常工作的概率 .
.
①求控制系统中正常工作的元件个数X的分布列和期望;
②在设备正常运行的条件下,求所有元件都正常工作的概率.
(2)请用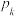 表示
表示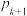 ,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
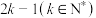 个相同的元件组成,每个元件正常工作的概率均为
个相同的元件组成,每个元件正常工作的概率均为 ,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为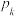 (例如:
(例如: 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).(1)若
 ,且每个元件正常工作的概率
,且每个元件正常工作的概率 .
.①求控制系统中正常工作的元件个数X的分布列和期望;
②在设备正常运行的条件下,求所有元件都正常工作的概率.
(2)请用
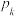 表示
表示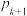 ,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
您最近一年使用:0次
9 . 设 都是不小于3的整数,当
都是不小于3的整数,当 时,
时,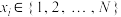 ,设集合
,设集合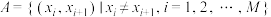 ,如果
,如果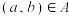 与
与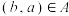 不能同时成立,则( )
不能同时成立,则( )
 都是不小于3的整数,当
都是不小于3的整数,当 时,
时,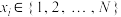 ,设集合
,设集合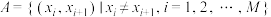 ,如果
,如果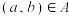 与
与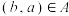 不能同时成立,则( )
不能同时成立,则( )A.若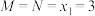 ,则 ,则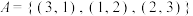 或 或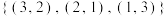 |
B.若 ,则 ,则 的可能取值为3或4或5 的可能取值为3或4或5 |
C.若 的值确定,则 的值确定,则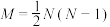 |
D.若 为奇数,则 为奇数,则 的最大值为 的最大值为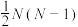 |
您最近一年使用:0次
名校
解题方法
10 . 人脸识别是基于人的脸部特征进行身份识别的一种生物识别技术.主要应用距离测试样本之间的相似度,常用测量距离的方式有3种.设 ,
, ,则欧几里得距离
,则欧几里得距离 ;曼哈顿距离
;曼哈顿距离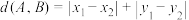 ,余弦距离
,余弦距离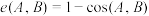 ,其中
,其中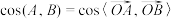 (
( 为坐标原点).
为坐标原点).
(1)若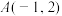 ,
,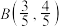 ,求
,求 ,
, 之间的曼哈顿距离
之间的曼哈顿距离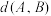 和余弦距离
和余弦距离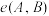 ;
;
(2)若点 ,
,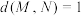 ,求
,求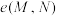 的最大值;
的最大值;
(3)已知点 ,
, 是直线
是直线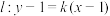 上的两动点,问是否存在直线
上的两动点,问是否存在直线 使得
使得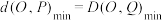 ,若存在,求出所有满足条件的直线
,若存在,求出所有满足条件的直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
 ,
, ,则欧几里得距离
,则欧几里得距离 ;曼哈顿距离
;曼哈顿距离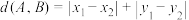 ,余弦距离
,余弦距离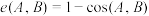 ,其中
,其中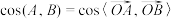 (
( 为坐标原点).
为坐标原点).(1)若
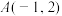 ,
,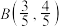 ,求
,求 ,
, 之间的曼哈顿距离
之间的曼哈顿距离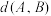 和余弦距离
和余弦距离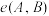 ;
;(2)若点
 ,
,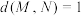 ,求
,求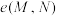 的最大值;
的最大值;(3)已知点
 ,
, 是直线
是直线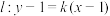 上的两动点,问是否存在直线
上的两动点,问是否存在直线 使得
使得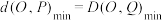 ,若存在,求出所有满足条件的直线
,若存在,求出所有满足条件的直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
您最近一年使用:0次



