解题方法
1 . 已知函数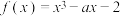 ,则( )
,则( )
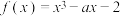 ,则( )
,则( )A.存在实数 使得 使得 |
B.当 时, 时, 有三个零点 有三个零点 |
C.点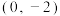 是曲线 是曲线 的对称中心 的对称中心 |
D.若曲线 有两条过点 有两条过点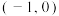 的切线,则 的切线,则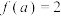 |
您最近一年使用:0次
解题方法
2 . 已知函数 .
.
(1)求曲线 在点
在点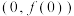 处的切线方程.
处的切线方程.
(2)若 ,且
,且 存在两个极值点
存在两个极值点 .
.
①求 的取值范围;
的取值范围;
②证明: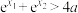 .
.
 .
.(1)求曲线
 在点
在点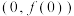 处的切线方程.
处的切线方程.(2)若
 ,且
,且 存在两个极值点
存在两个极值点 .
.①求
 的取值范围;
的取值范围;②证明:
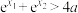 .
.
您最近一年使用:0次
3 . 已知函数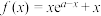 ,
, ,则( )
,则( )
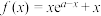 ,
, ,则( )
,则( )A. 在 在 上单调递增 上单调递增 |
B.当 时, 时, 有且只有一个极值点 有且只有一个极值点 |
C.若 有两个极值点,则 有两个极值点,则 |
D.若 有两个极值点 有两个极值点 , , ,则 ,则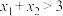 |
您最近一年使用:0次
名校
解题方法
4 . 已知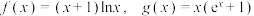 ,则下列结论正确的是( )
,则下列结论正确的是( )
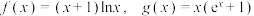 ,则下列结论正确的是( )
,则下列结论正确的是( )A.函数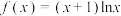 ,在 ,在 上存在唯一极值点 上存在唯一极值点 |
B.任意 ,有 ,有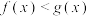 恒成立 恒成立 |
C.若对任意 ,不等式 ,不等式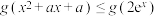 恒成立,则实数 恒成立,则实数 的最大值为2 的最大值为2 |
D.若 ,则 ,则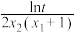 的最大值为 的最大值为 |
您最近一年使用:0次
2024高三下·全国·专题练习
解题方法
5 . 已知函数 .
.
(1)证明: ;
;
(2)若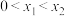 ,且
,且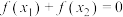 ,证明:
,证明: .
.
 .
.(1)证明:
 ;
;(2)若
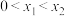 ,且
,且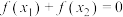 ,证明:
,证明: .
.
您最近一年使用:0次
解题方法
6 . (1)证明:当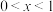 时,
时, ;
;
(2)已知函数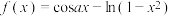 ,若
,若 是
是 的极小值点,求
的极小值点,求 的取值范围.
的取值范围.
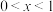 时,
时, ;
;(2)已知函数
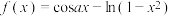 ,若
,若 是
是 的极小值点,求
的极小值点,求 的取值范围.
的取值范围.
您最近一年使用:0次
7 . 已知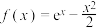 ,曲线
,曲线 在点
在点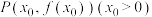 处的切线为
处的切线为 .
.
(1)当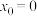 时,求直线
时,求直线 的方程;
的方程;
(2)证明: 与曲线
与曲线 有一个异于点
有一个异于点 的交点
的交点 ,且
,且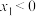 ;
;
(3)在(2)的条件下,令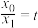 ,求
,求 的取值范围.
的取值范围.
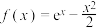 ,曲线
,曲线 在点
在点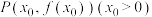 处的切线为
处的切线为 .
.(1)当
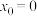 时,求直线
时,求直线 的方程;
的方程;(2)证明:
 与曲线
与曲线 有一个异于点
有一个异于点 的交点
的交点 ,且
,且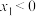 ;
;(3)在(2)的条件下,令
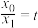 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
8 . 已知函数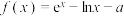 ,
, ,其中a为整数且
,其中a为整数且 .记
.记 为
为 的极值点,若
的极值点,若 存在两个不同的零点
存在两个不同的零点 ,
,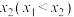 ,
,
(1)求a的最小值;
(2)求证: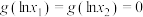 ;
;
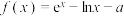 ,
, ,其中a为整数且
,其中a为整数且 .记
.记 为
为 的极值点,若
的极值点,若 存在两个不同的零点
存在两个不同的零点 ,
,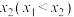 ,
,(1)求a的最小值;
(2)求证:
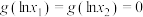 ;
;
您最近一年使用:0次
解题方法
9 . 已知函数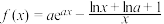 .
.
(1)当 时,请判断
时,请判断 的极值点的个数并说明理由;
的极值点的个数并说明理由;
(2)若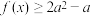 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
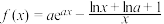 .
.(1)当
 时,请判断
时,请判断 的极值点的个数并说明理由;
的极值点的个数并说明理由;(2)若
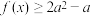 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
您最近一年使用:0次
名校
10 . 若函数 在
在 上单调递增,则
上单调递增,则 和
和 的可能取值为( )
的可能取值为( )
 在
在 上单调递增,则
上单调递增,则 和
和 的可能取值为( )
的可能取值为( )A.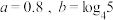 | B. |
C.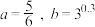 | D.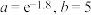 |
您最近一年使用:0次



