1 . 方程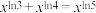 的正实数解为
的正实数解为______ .
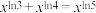 的正实数解为
的正实数解为
您最近一年使用:0次
2024-06-11更新
|
880次组卷
|
2卷引用:江苏省苏州外国语学校2023-2024学年高二下学期5月月考数学试题
解题方法
2 . 已知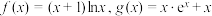 ,若存在
,若存在 ,使得
,使得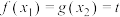 成立,则
成立,则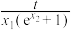 的最大值为
的最大值为_______ .
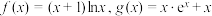 ,若存在
,若存在 ,使得
,使得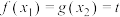 成立,则
成立,则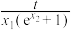 的最大值为
的最大值为
您最近一年使用:0次
解题方法
3 . 西附高中为了解“方洲路”,“普惠路”两个校区高二学生的数学水平,随机抽取200名学生进行调查统计,得到如下 列联表:
列联表:
(1)依据小概率值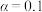 的
的 独立性检验,判断两校区学生的数学成绩优秀率是否有差异?
独立性检验,判断两校区学生的数学成绩优秀率是否有差异?
(2)西附高中不仅关注学生的学习成绩,更加注重学生的身心健康,德智体美劳全面发展.
①从上述参与调查的200人中按分层抽样从两校区抽出10人,再从10人中随机抽取3人参加“书记有约”活动,设其中来自“方洲路”的学生数为随机变量X,求随机变量X的分布列;
②为更好了解上述身体状况,将这200名同学排在一起逐个依次体检,己知每位同学体检所需时间为1分钟,求证:数学优秀同学体检全部结束所需时间 的期望
的期望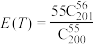 .
.
附:
 列联表:
列联表:优秀 | 不优秀 | 合计 | |
方洲路 | 30 | 90 | 120 |
普惠路 | 25 | 55 | 80 |
合计 | 55 | 145 | 200 |
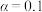 的
的 独立性检验,判断两校区学生的数学成绩优秀率是否有差异?
独立性检验,判断两校区学生的数学成绩优秀率是否有差异?(2)西附高中不仅关注学生的学习成绩,更加注重学生的身心健康,德智体美劳全面发展.
①从上述参与调查的200人中按分层抽样从两校区抽出10人,再从10人中随机抽取3人参加“书记有约”活动,设其中来自“方洲路”的学生数为随机变量X,求随机变量X的分布列;
②为更好了解上述身体状况,将这200名同学排在一起逐个依次体检,己知每位同学体检所需时间为1分钟,求证:数学优秀同学体检全部结束所需时间
 的期望
的期望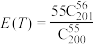 .
.附:

| 0.1 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
名校
4 . 已知函数 .
.
(1)当 时,求函数
时,求函数 的最小值;
的最小值;
(2)试讨论函数 的单调性;
的单调性;
(3)当 时,不等式
时,不等式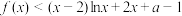 恒成立,求整数a的最大值.
恒成立,求整数a的最大值.
 .
.(1)当
 时,求函数
时,求函数 的最小值;
的最小值;(2)试讨论函数
 的单调性;
的单调性;(3)当
 时,不等式
时,不等式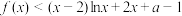 恒成立,求整数a的最大值.
恒成立,求整数a的最大值.
您最近一年使用:0次
5 . 已知函数 ,下列说法正确的是( )
,下列说法正确的是( )
 ,下列说法正确的是( )
,下列说法正确的是( )A.若 ,则 ,则 在 在 上单调递增 上单调递增 | B.若 为 为 的极大值点,则 的极大值点,则 |
C. 的图象经过一个定点 的图象经过一个定点 | D.若 ,则方程 ,则方程 有三个不相等的实数根 有三个不相等的实数根 |
您最近一年使用:0次
6 . 已知函数 .
.
(1)求函数 的导函数
的导函数 ;
;
(2)求函数 单调区间;
单调区间;
(3)若函数 有两个不同的极值点
有两个不同的极值点 ,记过
,记过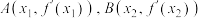 两点的直线斜率为
两点的直线斜率为 ,是否存在实数
,是否存在实数 ,使得
,使得 ,若存在,求实数
,若存在,求实数 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
 .
.(1)求函数
 的导函数
的导函数 ;
;(2)求函数
 单调区间;
单调区间;(3)若函数
 有两个不同的极值点
有两个不同的极值点 ,记过
,记过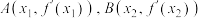 两点的直线斜率为
两点的直线斜率为 ,是否存在实数
,是否存在实数 ,使得
,使得 ,若存在,求实数
,若存在,求实数 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
您最近一年使用:0次
2024-04-27更新
|
430次组卷
|
3卷引用:江苏省苏州市2023-2024学年高二下学期4月期中调研数学试题
名校
7 . 甲、乙两人进行知识问答比赛,共有 道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为
道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为 和
和 ,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.
,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.
(1)若 ,
, ,求甲获胜的概率;
,求甲获胜的概率;
(2)若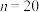 ,设甲第
,设甲第 题的得分为随机变量
题的得分为随机变量 ,一次比赛中得到
,一次比赛中得到 的一组观测值
的一组观测值 ,如下表.现利用统计方法来估计
,如下表.现利用统计方法来估计 的值:
的值:
①设随机变量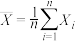 ,若以观测值
,若以观测值 的均值
的均值 作为
作为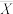 的数学期望,请以此求出
的数学期望,请以此求出 的估计值
的估计值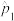 ;
;
②设随机变量 取到观测值
取到观测值 的概率为
的概率为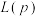 ,即
,即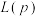
 ;在一次抽样中获得这一组特殊观测值的概率应该最大,随着
;在一次抽样中获得这一组特殊观测值的概率应该最大,随着 的变化,用使得
的变化,用使得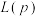 达到最大时
达到最大时 的取值
的取值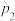 作为参数
作为参数 的一个估计值.求
的一个估计值.求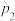 .
.
表1:甲得分的一组观测值.
附:若随机变量 ,
, 的期望
的期望 ,
, 都存在,则
都存在,则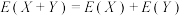 .
.
 道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为
道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为 和
和 ,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.
,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.(1)若
 ,
, ,求甲获胜的概率;
,求甲获胜的概率;(2)若
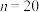 ,设甲第
,设甲第 题的得分为随机变量
题的得分为随机变量 ,一次比赛中得到
,一次比赛中得到 的一组观测值
的一组观测值 ,如下表.现利用统计方法来估计
,如下表.现利用统计方法来估计 的值:
的值:①设随机变量
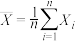 ,若以观测值
,若以观测值 的均值
的均值 作为
作为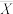 的数学期望,请以此求出
的数学期望,请以此求出 的估计值
的估计值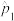 ;
;②设随机变量
 取到观测值
取到观测值 的概率为
的概率为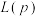 ,即
,即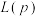
 ;在一次抽样中获得这一组特殊观测值的概率应该最大,随着
;在一次抽样中获得这一组特殊观测值的概率应该最大,随着 的变化,用使得
的变化,用使得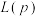 达到最大时
达到最大时 的取值
的取值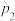 作为参数
作为参数 的一个估计值.求
的一个估计值.求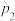 .
.| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分 | 1 | 0 | 0 | ﹣1 | 1 | 1 | ﹣1 | 0 | 0 | 0 |
| 题目 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 得分 | ﹣1 | 0 | 1 | 1 | ﹣1 | 0 | 0 | 0 | 1 | 0 |
附:若随机变量
 ,
, 的期望
的期望 ,
, 都存在,则
都存在,则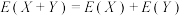 .
.
您最近一年使用:0次
2024-04-19更新
|
2761次组卷
|
8卷引用:江苏省苏州实验中学2023-2024学年高二下学期5月月考数学试题
江苏省苏州实验中学2023-2024学年高二下学期5月月考数学试题(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)浙江省天域全国名校协作体2023-2024学年高三二模数学试题山东省青岛第二中学2024届高三下学期二模考试数学试题(已下线)数学(江苏专用02)河北省重点高中2024届高三下学期5月模拟考试数学试题(一)(已下线)模块4 二模重组卷 第6套 全真模拟卷广东省广州市执信中学2024届高三下学期教学情况检测(三)数学试题
名校
8 . 已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若存在正数 ,使
,使 成立,求
成立,求 的取值范围;
的取值范围;
(3)若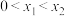 ,证明:对任意
,证明:对任意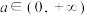 ,存在唯一的实数
,存在唯一的实数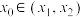 ,使得
,使得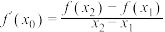 成立.
成立.
 .
.(1)讨论函数
 的单调性;
的单调性;(2)若存在正数
 ,使
,使 成立,求
成立,求 的取值范围;
的取值范围;(3)若
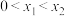 ,证明:对任意
,证明:对任意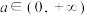 ,存在唯一的实数
,存在唯一的实数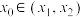 ,使得
,使得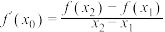 成立.
成立.
您最近一年使用:0次
2024-04-18更新
|
1735次组卷
|
4卷引用:江苏省苏州实验中学2023-2024学年高二下学期5月月考数学试题
2024高三·河南·专题练习
9 . 设函数 ,
,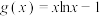 ,
,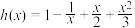 在
在 上的零点分别为
上的零点分别为 ,则
,则 的大小顺序为( )
的大小顺序为( )
 ,
,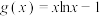 ,
,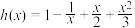 在
在 上的零点分别为
上的零点分别为 ,则
,则 的大小顺序为( )
的大小顺序为( )A.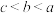 | B.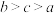 |
C.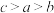 | D.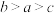 |
您最近一年使用:0次
2024-04-16更新
|
539次组卷
|
3卷引用:江苏省苏州市常熟省中2023-2024学年高二下学期3月月考数学试题
名校
解题方法
10 . 已知函数 ,其中a为正实数.
,其中a为正实数.
(1)若函数 有极值点,求a的取值范围;
有极值点,求a的取值范围;
(2)当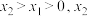 和
和 的几何平均数为
的几何平均数为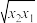 ,算术平均数为
,算术平均数为 .
.
①判断 与
与 和
和 的几何平均数和算术平均数的大小关系,并加以证明;
的几何平均数和算术平均数的大小关系,并加以证明;
②当 时,证明:
时,证明: .
.
 ,其中a为正实数.
,其中a为正实数.(1)若函数
 有极值点,求a的取值范围;
有极值点,求a的取值范围;(2)当
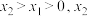 和
和 的几何平均数为
的几何平均数为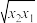 ,算术平均数为
,算术平均数为 .
. ①判断
 与
与 和
和 的几何平均数和算术平均数的大小关系,并加以证明;
的几何平均数和算术平均数的大小关系,并加以证明;②当
 时,证明:
时,证明: .
.
您最近一年使用:0次





