1 . 已知抛物线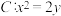 ,动圆
,动圆

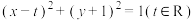 ,
, 为抛物线
为抛物线 上一动点,过点
上一动点,过点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.
(1)若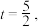 求
求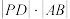 的最小值;
的最小值;
(2)若过圆心 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为 .
.
(Ⅰ)求证:直线 过定点;
过定点;
(Ⅱ)若线段 的中点为
的中点为 ,连
,连 交抛物线
交抛物线 于点
于点 ,记
,记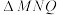 的面积为
的面积为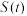 ,求
,求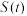 的表达式及其最小值.
的表达式及其最小值.
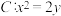 ,动圆
,动圆

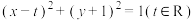 ,
, 为抛物线
为抛物线 上一动点,过点
上一动点,过点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.(1)若
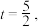 求
求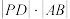 的最小值;
的最小值;(2)若过圆心
 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为 .
.(Ⅰ)求证:直线
 过定点;
过定点;(Ⅱ)若线段
 的中点为
的中点为 ,连
,连 交抛物线
交抛物线 于点
于点 ,记
,记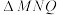 的面积为
的面积为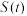 ,求
,求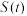 的表达式及其最小值.
的表达式及其最小值.
您最近一年使用:0次
名校
2 . 若数列 满足
满足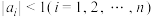 ,则称该数列为边界为1的数列.对于边界为1的有穷数列
,则称该数列为边界为1的数列.对于边界为1的有穷数列 ,从该数列中任意去掉两项
,从该数列中任意去掉两项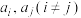 ,同时添加
,同时添加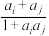 作为该数列的末项,可以得到一个项数为
作为该数列的末项,可以得到一个项数为 项的新数列,称此过程为对数列
项的新数列,称此过程为对数列 实施一次“降维”.规定这种“降维”只能实施于边界为1的数列.如果数列
实施一次“降维”.规定这种“降维”只能实施于边界为1的数列.如果数列 经过若干次“降维”后成为只有一项的数列,即得到一个实数,则称该实数为数列
经过若干次“降维”后成为只有一项的数列,即得到一个实数,则称该实数为数列 的一个“坍缩数”.
的一个“坍缩数”.
(1)设数列 的递推公式为
的递推公式为 ,我们知道:当
,我们知道:当 取不同的值时,可以得到不同的数列,若
取不同的值时,可以得到不同的数列,若 取某实数时,该数列是一个只有3项的有穷数列,求该数列的所有可能的“坍缩数”.
取某实数时,该数列是一个只有3项的有穷数列,求该数列的所有可能的“坍缩数”.
(2)试证明:对于任意一个边界为1的有穷数列 ,都可以对其持续进行“降维”,直至得到该数列的一个“坍缩数”.
,都可以对其持续进行“降维”,直至得到该数列的一个“坍缩数”.
(3)若数列 的共有
的共有 项,其通项公式为
项,其通项公式为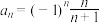 ,求证:当
,求证:当 为偶数时,数列
为偶数时,数列 的“坍缩数”一定为正;当
的“坍缩数”一定为正;当 为奇数时,数列
为奇数时,数列 的“坍缩数”一定为负.
的“坍缩数”一定为负.
 满足
满足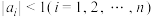 ,则称该数列为边界为1的数列.对于边界为1的有穷数列
,则称该数列为边界为1的数列.对于边界为1的有穷数列 ,从该数列中任意去掉两项
,从该数列中任意去掉两项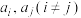 ,同时添加
,同时添加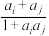 作为该数列的末项,可以得到一个项数为
作为该数列的末项,可以得到一个项数为 项的新数列,称此过程为对数列
项的新数列,称此过程为对数列 实施一次“降维”.规定这种“降维”只能实施于边界为1的数列.如果数列
实施一次“降维”.规定这种“降维”只能实施于边界为1的数列.如果数列 经过若干次“降维”后成为只有一项的数列,即得到一个实数,则称该实数为数列
经过若干次“降维”后成为只有一项的数列,即得到一个实数,则称该实数为数列 的一个“坍缩数”.
的一个“坍缩数”.(1)设数列
 的递推公式为
的递推公式为 ,我们知道:当
,我们知道:当 取不同的值时,可以得到不同的数列,若
取不同的值时,可以得到不同的数列,若 取某实数时,该数列是一个只有3项的有穷数列,求该数列的所有可能的“坍缩数”.
取某实数时,该数列是一个只有3项的有穷数列,求该数列的所有可能的“坍缩数”.(2)试证明:对于任意一个边界为1的有穷数列
 ,都可以对其持续进行“降维”,直至得到该数列的一个“坍缩数”.
,都可以对其持续进行“降维”,直至得到该数列的一个“坍缩数”.(3)若数列
 的共有
的共有 项,其通项公式为
项,其通项公式为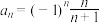 ,求证:当
,求证:当 为偶数时,数列
为偶数时,数列 的“坍缩数”一定为正;当
的“坍缩数”一定为正;当 为奇数时,数列
为奇数时,数列 的“坍缩数”一定为负.
的“坍缩数”一定为负.
您最近一年使用:0次
3 . 在微积分中,泰勒展开是一种常用的分析方法.若 在包含
在包含 的某个开区间
的某个开区间 中具有
中具有 阶导数,设
阶导数,设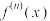 表示
表示 的
的 阶导数.则对
阶导数.则对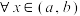 有
有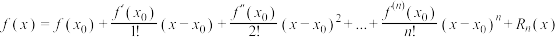 .其中
.其中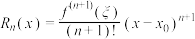 ,
, 是位于
是位于 与
与 之间的某个值,它称为
之间的某个值,它称为 阶泰勒余项.
阶泰勒余项.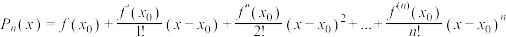 叫做
叫做 在
在 处的
处的 阶泰勒多项式.
阶泰勒多项式.
(1)求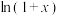 在
在 处的1阶泰勒多项式
处的1阶泰勒多项式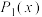 和2阶泰勒多项式
和2阶泰勒多项式 ,并证明:当
,并证明:当 时,
时,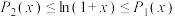 ;
;
(2)整数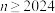 .定义数列
.定义数列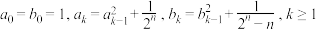 .设e为自然对数的底数.
.设e为自然对数的底数.
(i)求证: ;
;
(ii)求证: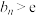 .
.
 在包含
在包含 的某个开区间
的某个开区间 中具有
中具有 阶导数,设
阶导数,设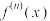 表示
表示 的
的 阶导数.则对
阶导数.则对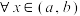 有
有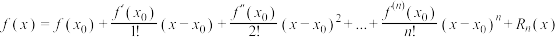 .其中
.其中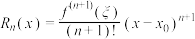 ,
, 是位于
是位于 与
与 之间的某个值,它称为
之间的某个值,它称为 阶泰勒余项.
阶泰勒余项.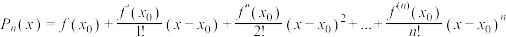 叫做
叫做 在
在 处的
处的 阶泰勒多项式.
阶泰勒多项式.(1)求
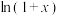 在
在 处的1阶泰勒多项式
处的1阶泰勒多项式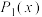 和2阶泰勒多项式
和2阶泰勒多项式 ,并证明:当
,并证明:当 时,
时,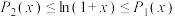 ;
;(2)整数
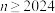 .定义数列
.定义数列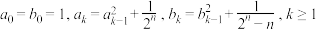 .设e为自然对数的底数.
.设e为自然对数的底数. (i)求证:
 ;
;(ii)求证:
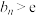 .
.
您最近一年使用:0次
解题方法
4 . “友谊杯”围棋擂台赛采取淘汰制,现有 名选手报名参加比赛(含甲、乙两名选手),规则如下:第一轮将所有报名选手任意两两配对对弈,输者淘汰出局,然后将剩下的
名选手报名参加比赛(含甲、乙两名选手),规则如下:第一轮将所有报名选手任意两两配对对弈,输者淘汰出局,然后将剩下的 名胜者再任意两两配对对弈,同样输者淘汰出局……如此下去,直至第
名胜者再任意两两配对对弈,同样输者淘汰出局……如此下去,直至第 轮比赛决出一名冠军.假定每名选手在各轮比赛中获胜的概率均为0.5.
轮比赛决出一名冠军.假定每名选手在各轮比赛中获胜的概率均为0.5.
(1)当 时,求甲、乙两人相遇对弈的概率
时,求甲、乙两人相遇对弈的概率 ;
;
(2)当 时,求甲、乙两人相遇对弈的概率
时,求甲、乙两人相遇对弈的概率 ;
;
(3)已知当擂台赛报名选手人数分别为 时,甲、乙两人相遇对弈的次数依次是
时,甲、乙两人相遇对弈的次数依次是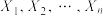 ,记
,记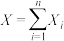 ,若随机变量
,若随机变量 服从两点分布,且
服从两点分布,且 ,
,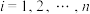 ,求
,求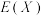 .
.
 名选手报名参加比赛(含甲、乙两名选手),规则如下:第一轮将所有报名选手任意两两配对对弈,输者淘汰出局,然后将剩下的
名选手报名参加比赛(含甲、乙两名选手),规则如下:第一轮将所有报名选手任意两两配对对弈,输者淘汰出局,然后将剩下的 名胜者再任意两两配对对弈,同样输者淘汰出局……如此下去,直至第
名胜者再任意两两配对对弈,同样输者淘汰出局……如此下去,直至第 轮比赛决出一名冠军.假定每名选手在各轮比赛中获胜的概率均为0.5.
轮比赛决出一名冠军.假定每名选手在各轮比赛中获胜的概率均为0.5.(1)当
 时,求甲、乙两人相遇对弈的概率
时,求甲、乙两人相遇对弈的概率 ;
;(2)当
 时,求甲、乙两人相遇对弈的概率
时,求甲、乙两人相遇对弈的概率 ;
;(3)已知当擂台赛报名选手人数分别为
 时,甲、乙两人相遇对弈的次数依次是
时,甲、乙两人相遇对弈的次数依次是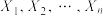 ,记
,记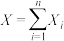 ,若随机变量
,若随机变量 服从两点分布,且
服从两点分布,且 ,
,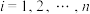 ,求
,求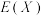 .
.
您最近一年使用:0次
名校
5 . 设函数 的定义域为
的定义域为 .给定闭区间
.给定闭区间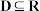 ,若存在
,若存在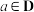 ,使得对于任意
,使得对于任意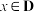 ,
,
①均有 ,则记
,则记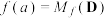 ;
;
②均有 ,则记
,则记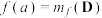 .
.
(1)设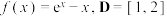 ,求
,求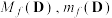 ;
;
(2)设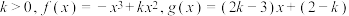 .若对于任意
.若对于任意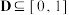 ,均有
,均有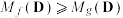 ,求
,求 的取值范围;
的取值范围;
(3)已知对于任意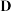 ⫋
⫋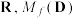 与
与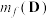 均存在.证明:“
均存在.证明:“ 为
为 上的增函数或减函数”的充要条件为“对于任意两个不同的
上的增函数或减函数”的充要条件为“对于任意两个不同的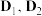 ⫋
⫋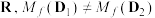 与
与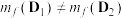 中至少一个成立”.
中至少一个成立”.
 的定义域为
的定义域为 .给定闭区间
.给定闭区间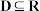 ,若存在
,若存在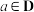 ,使得对于任意
,使得对于任意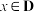 ,
,①均有
 ,则记
,则记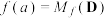 ;
;②均有
 ,则记
,则记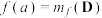 .
.(1)设
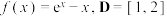 ,求
,求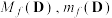 ;
;(2)设
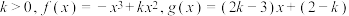 .若对于任意
.若对于任意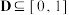 ,均有
,均有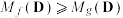 ,求
,求 的取值范围;
的取值范围;(3)已知对于任意
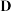 ⫋
⫋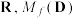 与
与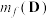 均存在.证明:“
均存在.证明:“ 为
为 上的增函数或减函数”的充要条件为“对于任意两个不同的
上的增函数或减函数”的充要条件为“对于任意两个不同的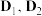 ⫋
⫋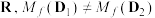 与
与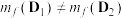 中至少一个成立”.
中至少一个成立”.
您最近一年使用:0次
2024-06-11更新
|
374次组卷
|
2卷引用:安徽省阜阳市北外附属新华外国语高级中学2025届高三上学期第一次段考数学试卷
名校
6 . 若数列 的各项均为正数,且对任意的相邻三项
的各项均为正数,且对任意的相邻三项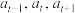 ,都满足
,都满足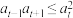 ,则称该数列为“对数性凸数列”,若对任意的相邻三项
,则称该数列为“对数性凸数列”,若对任意的相邻三项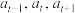 ,都满足
,都满足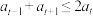 则称该数列为“凸数列”.
则称该数列为“凸数列”.
(1)已知正项数列 是一个“凸数列”,且
是一个“凸数列”,且 ,(其中
,(其中 为自然常数,
为自然常数, ),证明:数列
),证明:数列 是一个“对数性凸数列”,且有
是一个“对数性凸数列”,且有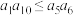 ;
;
(2)若关于 的函数
的函数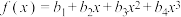 有三个零点,其中
有三个零点,其中 .证明:数列
.证明:数列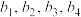 是一个“对数性凸数列”:
是一个“对数性凸数列”:
(3)设正项数列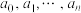 是一个“对数性凸数列”,求证:
是一个“对数性凸数列”,求证:
 的各项均为正数,且对任意的相邻三项
的各项均为正数,且对任意的相邻三项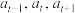 ,都满足
,都满足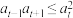 ,则称该数列为“对数性凸数列”,若对任意的相邻三项
,则称该数列为“对数性凸数列”,若对任意的相邻三项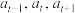 ,都满足
,都满足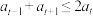 则称该数列为“凸数列”.
则称该数列为“凸数列”.(1)已知正项数列
 是一个“凸数列”,且
是一个“凸数列”,且 ,(其中
,(其中 为自然常数,
为自然常数, ),证明:数列
),证明:数列 是一个“对数性凸数列”,且有
是一个“对数性凸数列”,且有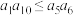 ;
;(2)若关于
 的函数
的函数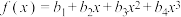 有三个零点,其中
有三个零点,其中 .证明:数列
.证明:数列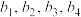 是一个“对数性凸数列”:
是一个“对数性凸数列”:(3)设正项数列
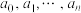 是一个“对数性凸数列”,求证:
是一个“对数性凸数列”,求证:
您最近一年使用:0次
7 . 在不大于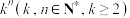 的正整数中,所有既不能被2整除也不能被3整除的个数记为
的正整数中,所有既不能被2整除也不能被3整除的个数记为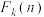 .
.
(1)求 ,
,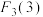 的值;
的值;
(2)对于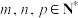 ,
,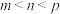 ,是否存在m,n,p,使得
,是否存在m,n,p,使得 ?若存在,求出m,n,p的值;若不存在,请说明理由;
?若存在,求出m,n,p的值;若不存在,请说明理由;
(3)记 表示不超过
表示不超过 的最大整数,且
的最大整数,且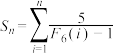 ,求
,求 的值.
的值.
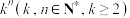 的正整数中,所有既不能被2整除也不能被3整除的个数记为
的正整数中,所有既不能被2整除也不能被3整除的个数记为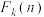 .
.(1)求
 ,
,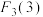 的值;
的值;(2)对于
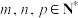 ,
,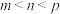 ,是否存在m,n,p,使得
,是否存在m,n,p,使得 ?若存在,求出m,n,p的值;若不存在,请说明理由;
?若存在,求出m,n,p的值;若不存在,请说明理由;(3)记
 表示不超过
表示不超过 的最大整数,且
的最大整数,且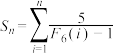 ,求
,求 的值.
的值.
您最近一年使用:0次
2024-06-07更新
|
645次组卷
|
3卷引用:安徽省A10联盟2024届高三4月质量检测考试数学试题
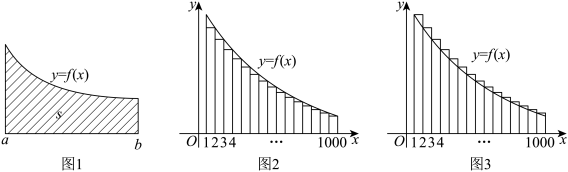
8 . 若 为
为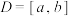 上的非负图像连续的函数,点
上的非负图像连续的函数,点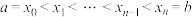 将区间
将区间 划分为
划分为 个长度为
个长度为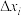 的小区间
的小区间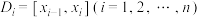 .记
.记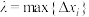 ,若无穷和的极限
,若无穷和的极限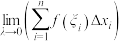 存在
存在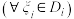 ,并称其为区域
,并称其为区域 的精确面积,记为
的精确面积,记为 .
.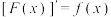 ,则
,则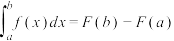 .求由直线
.求由直线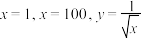 以及轴所围成封闭图形面积;
以及轴所围成封闭图形面积;
(2)若区间 被等分为
被等分为 个小区间,请推证:
个小区间,请推证: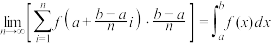 .并由此计算无穷和极限
.并由此计算无穷和极限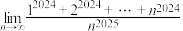 的值;
的值;
(3)求有限项和式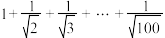 的整数部分.
的整数部分.
 为
为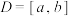 上的非负图像连续的函数,点
上的非负图像连续的函数,点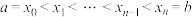 将区间
将区间 划分为
划分为 个长度为
个长度为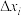 的小区间
的小区间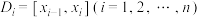 .记
.记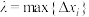 ,若无穷和的极限
,若无穷和的极限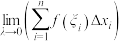 存在
存在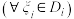 ,并称其为区域
,并称其为区域 的精确面积,记为
的精确面积,记为 .
.
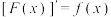 ,则
,则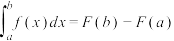 .求由直线
.求由直线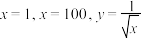 以及轴所围成封闭图形面积;
以及轴所围成封闭图形面积;(2)若区间
 被等分为
被等分为 个小区间,请推证:
个小区间,请推证: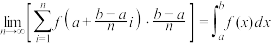 .并由此计算无穷和极限
.并由此计算无穷和极限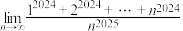 的值;
的值;(3)求有限项和式
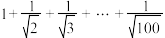 的整数部分.
的整数部分.
您最近一年使用:0次
2024-06-04更新
|
293次组卷
|
3卷引用:安徽省合肥一六八中学2024届高三最后一卷数学试题
名校
9 . 贝塞尔曲线(Be'zier curve)是一种广泛应用于计算机图形学、动画制作、CAD设计以及相关领域的数学曲线.它最早来源于Bernstein多项式.引入多项式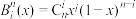
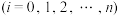 ,若
,若 是定义在
是定义在 上的函数,称
上的函数,称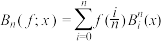 ,
, 为函数
为函数 的n次Bernstein多项式.
的n次Bernstein多项式.
(1)求 在
在 上取得最大值时x的值;
上取得最大值时x的值;
(2)当 时,先化简
时,先化简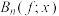 ,再求
,再求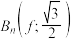 的值;
的值;
(3)设 ,
,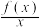 在
在 内单调递增,求证:
内单调递增,求证: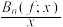 在
在 内也单调递增.
内也单调递增.
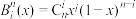
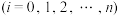 ,若
,若 是定义在
是定义在 上的函数,称
上的函数,称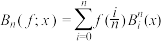 ,
, 为函数
为函数 的n次Bernstein多项式.
的n次Bernstein多项式.(1)求
 在
在 上取得最大值时x的值;
上取得最大值时x的值;(2)当
 时,先化简
时,先化简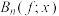 ,再求
,再求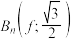 的值;
的值;(3)设
 ,
,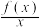 在
在 内单调递增,求证:
内单调递增,求证: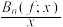 在
在 内也单调递增.
内也单调递增.
您最近一年使用:0次
解题方法
10 . 已知数列 的前n项和为
的前n项和为 ,若数列
,若数列 满足:
满足:
①数列 为有穷数列;
为有穷数列;
②数列 为递增数列;
为递增数列;
③ ,
, ,
,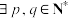 ,使得
,使得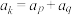 ;
;
则称数列 具有“和性质”.
具有“和性质”.
(1)已知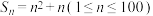 ,求数列
,求数列 的通项公式,并判断数列
的通项公式,并判断数列 是否具有“和性质”;(判断是否具有“和性质”时不必说明理由,直接给出结论)
是否具有“和性质”;(判断是否具有“和性质”时不必说明理由,直接给出结论)
(2)若首项为1的数列 具有“和性质”.
具有“和性质”.
(ⅰ)比较 与
与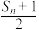 的大小关系,并说明理由;
的大小关系,并说明理由;
(ⅱ)若数列 的末项为36,求
的末项为36,求 的最小值.
的最小值.
 的前n项和为
的前n项和为 ,若数列
,若数列 满足:
满足:①数列
 为有穷数列;
为有穷数列;②数列
 为递增数列;
为递增数列;③
 ,
, ,
,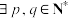 ,使得
,使得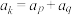 ;
;则称数列
 具有“和性质”.
具有“和性质”.(1)已知
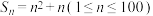 ,求数列
,求数列 的通项公式,并判断数列
的通项公式,并判断数列 是否具有“和性质”;(判断是否具有“和性质”时不必说明理由,直接给出结论)
是否具有“和性质”;(判断是否具有“和性质”时不必说明理由,直接给出结论)(2)若首项为1的数列
 具有“和性质”.
具有“和性质”.(ⅰ)比较
 与
与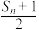 的大小关系,并说明理由;
的大小关系,并说明理由;(ⅱ)若数列
 的末项为36,求
的末项为36,求 的最小值.
的最小值.
您最近一年使用:0次



