名校
解题方法
1 . 已知O为坐标原点,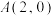 ,
, ,
, ,P,Q分别是线段
,P,Q分别是线段 ,
, 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )
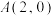 ,
, ,
, ,P,Q分别是线段
,P,Q分别是线段 ,
, 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )A.点M到直线 的距离为 的距离为 | B.若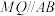 ,则点Q的坐标为 ,则点Q的坐标为 |
C.点M关于直线 对称的点的坐标为 对称的点的坐标为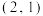 | D. 周长的最小值为 周长的最小值为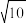 |
您最近一年使用:0次
2023-09-30更新
|
496次组卷
|
5卷引用:广东省阳江市2023-2024学年高二上学期期中数学试题
广东省阳江市2023-2024学年高二上学期期中数学试题河南省青桐鸣2023-2024学年高二上学期9月大联考数学试题安徽省合肥市第九中学2023-2024学年高二上学期第一次单元质量检测数学试题(已下线)专题14 直线的交点坐标与距离公式10种常见考法归类(2)(已下线)第2讲:各类对称问题的应用【练】
名校
2 . 已知 ,下列说法正确的是( )
,下列说法正确的是( )
 ,下列说法正确的是( )
,下列说法正确的是( )A.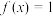 时, 时, |
B.若方程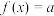 有两个根,则 有两个根,则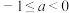 |
C.若直线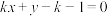 与 与 有两个交点,则 有两个交点,则 或 或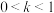 |
D.函数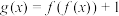 有3个零点 有3个零点 |
您最近一年使用:0次
2023-09-23更新
|
1045次组卷
|
5卷引用:广东省阳江市2023-2024学年高二上学期期中数学试题
广东省阳江市2023-2024学年高二上学期期中数学试题 吉林省长春市东北师范大学附属中学2023-2024学年高三上学期第一次摸底考试数学试题(已下线)第2章 直线和圆的方程单元测试能力卷-2023-2024学年高二数学上学期人教A版(2019)选择性必修第一册(已下线)专题02 直线和圆的方程(5)(已下线)专题17 直线与圆小题
3 . 为了学习、宣传和践行党的二十大精神,某班组织全班学生开展了以“学党史、知国情、圆梦想”为主题的党史暨时政知识竞赛活动.已知该班男生 人,女生
人,女生 人,根据统计分析,男生组成绩和女生组成绩的方差分别为
人,根据统计分析,男生组成绩和女生组成绩的方差分别为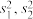 .记该班成绩的方差为
.记该班成绩的方差为 ,则下列判断正确的是( )
,则下列判断正确的是( )
 人,女生
人,女生 人,根据统计分析,男生组成绩和女生组成绩的方差分别为
人,根据统计分析,男生组成绩和女生组成绩的方差分别为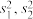 .记该班成绩的方差为
.记该班成绩的方差为 ,则下列判断正确的是( )
,则下列判断正确的是( )A.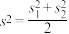 | B.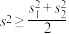 | C.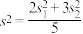 | D.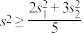 |
您最近一年使用:0次
2023-09-05更新
|
875次组卷
|
10卷引用:广东省阳江市2023-2024学年高二上学期期中数学试题
广东省阳江市2023-2024学年高二上学期期中数学试题江西省九江市2023届高三一模数学(理)试题新疆阿克苏地区库车市第二中学2023-2024学年高二上学期第一次月数学试题(已下线)第六章 统计章末测试--同步精品课堂(北师大版2019必修第一册)(已下线)第01讲 统计(练习)(已下线)专题13 统计与随机变量及其分布小题综合(已下线)专题08 统计案例分析(讲义)(已下线)第九章 统计-【上好课】(人教A版2019必修第二册)(已下线)9.2.4?总体离散程度的估计——课后作业(提升版)(已下线)第06讲 9.2.4 总体离散程度的估计-【帮课堂】(人教A版2019必修第二册)
名校
4 . 新高考数学试卷中的多项选择题,给出的4个选项中有2个以上选项是正确的,每一道题考生全部选对得5分. 对而不全得2分,选项中有错误得0分. 设一套数学试卷的多选题中有2个选项正确的概率为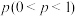 ,有3个选项正确的概率为
,有3个选项正确的概率为 ,没有4个选项都正确的(在本问题中认为其概率为0). 在一次模拟考试中:
,没有4个选项都正确的(在本问题中认为其概率为0). 在一次模拟考试中:
(1)小明可以确认一道多选题的选项A是错误的,从其余的三个选项中随机选择2个作为答案,若小明该题得5分的概率为 ,求
,求 ;
;
(2)小明可以确认另一道多选题的选项A是正确的,其余的选项只能随机选择. 小明有三种方案:①只选A不再选择其他答案;②从另外三个选项中再随机选择1个,共选2个;③从另外三个选项中再随机选择2个,共选3个. 若 ,以最后得分的数学期望为决策依据,小明应该选择哪个方案?
,以最后得分的数学期望为决策依据,小明应该选择哪个方案?
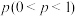 ,有3个选项正确的概率为
,有3个选项正确的概率为 ,没有4个选项都正确的(在本问题中认为其概率为0). 在一次模拟考试中:
,没有4个选项都正确的(在本问题中认为其概率为0). 在一次模拟考试中:(1)小明可以确认一道多选题的选项A是错误的,从其余的三个选项中随机选择2个作为答案,若小明该题得5分的概率为
 ,求
,求 ;
;(2)小明可以确认另一道多选题的选项A是正确的,其余的选项只能随机选择. 小明有三种方案:①只选A不再选择其他答案;②从另外三个选项中再随机选择1个,共选2个;③从另外三个选项中再随机选择2个,共选3个. 若
 ,以最后得分的数学期望为决策依据,小明应该选择哪个方案?
,以最后得分的数学期望为决策依据,小明应该选择哪个方案?
您最近一年使用:0次
2023-07-04更新
|
1143次组卷
|
9卷引用:广东省阳江市2022-2023学年高二下学期期末数学试题
广东省阳江市2022-2023学年高二下学期期末数学试题湖南省怀化市2022-2023学年高二下学期期末数学试题江西省上高中学2022-2023学年高二下学期7月期末数学试题四川省绵阳市高中2024届高三突击班第零次诊断性考试理科数学试题云南省长水教育集团2024届高三上学期10月质量检测数学试题(已下线)考点巩固卷26分布列及三大分布(十一大考点)-2(已下线)高二下学期期末数学试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)高二下学期期末复习解答题压轴题二十二大题型专练(4)【人教A版(2019)】专题14概率与统计(第四部分)-高二下学期名校期末好题汇编
5 . 抛物线C: ,AB是C的焦点弦( )
,AB是C的焦点弦( )
 ,AB是C的焦点弦( )
,AB是C的焦点弦( )A.点P在C的准线上,则 的最小值为0 的最小值为0 |
| B.以AB为直径的所有圆中,圆面积的最小值为9π |
C.若AB的斜率 ,则△ABO的面积 ,则△ABO的面积 |
D.存在一个半径为 的定圆与以AB为直径的圆都内切 的定圆与以AB为直径的圆都内切 |
您最近一年使用:0次
2023-06-25更新
|
808次组卷
|
4卷引用:广东省阳江市2024届高三上学期第一次阶段调研数学试题
广东省阳江市2024届高三上学期第一次阶段调研数学试题福建省福州第一中学2023届高三适应性考试(三)数学试题(已下线)3.3 抛物线(精练)-2023-2024学年高二数学《一隅三反》系列(人教A版2019选择性必修第一册)(已下线)专题11 平面解析几何-2
解题方法
6 . 一个不透明的袋子中装有大小形状完全相同的红、黄、蓝三种颜色的小球各一个,每次从袋子中随机摸出一个小球,记录颜色后放回,当三种颜色的小球均被摸出过时就停止摸球.设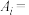 “第i次摸到红球”,
“第i次摸到红球”,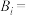 “第i次摸到黄球”,
“第i次摸到黄球”, “第i次摸到蓝球”,
“第i次摸到蓝球”,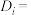 “摸完第i次球后就停止摸球”,则( )
“摸完第i次球后就停止摸球”,则( )
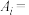 “第i次摸到红球”,
“第i次摸到红球”,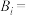 “第i次摸到黄球”,
“第i次摸到黄球”, “第i次摸到蓝球”,
“第i次摸到蓝球”,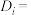 “摸完第i次球后就停止摸球”,则( )
“摸完第i次球后就停止摸球”,则( )A.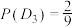 | B. |
C.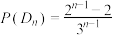 , , | D.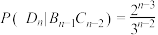 , , |
您最近一年使用:0次
2023-06-23更新
|
1452次组卷
|
5卷引用:广东省阳江市2022-2023学年高二下学期期末数学试题
广东省阳江市2022-2023学年高二下学期期末数学试题浙江省宁波市九校2022-2023学年高二下学期期末联考数学试题(已下线)专题03 条件概率与全概率公式(1)(已下线)专题7.10 随机变量及其分布全章综合测试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题02概率统计期末10种常考题型归类【好题汇编】-备战2023-2024学年高二数学下学期期末真题分类汇编(人教B版2019选择性必修第二册)
7 . 某科研单位研制出某型号科考飞艇,一艘该型号飞艇最多只能执行 次
次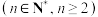 科考任务,一艘该型号飞艇第1次执行科考任务,能成功返航的概率为
科考任务,一艘该型号飞艇第1次执行科考任务,能成功返航的概率为 ,若第
,若第 次
次 执行科考任务能成功返航,则执行第
执行科考任务能成功返航,则执行第 次科考任务且能成功返航的概率也为
次科考任务且能成功返航的概率也为 ,否则此飞艇结束科考任务.一艘该型号飞艇每次执行科考任务,若能成功返航,则可获得价值为
,否则此飞艇结束科考任务.一艘该型号飞艇每次执行科考任务,若能成功返航,则可获得价值为 万元的科考数据,且“
万元的科考数据,且“ ”的概率为0.8,“
”的概率为0.8,“ ”的概率为0.2;若不能成功返航,则此次科考任务不能获得任何科考数据.记一艘该型号飞艇共可获得的科考数据的总价值为
”的概率为0.2;若不能成功返航,则此次科考任务不能获得任何科考数据.记一艘该型号飞艇共可获得的科考数据的总价值为 万元.
万元.
(1)若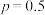 ,
, ,求
,求 的分布列;
的分布列;
(2)求 (用
(用 和
和 表示).
表示).
 次
次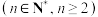 科考任务,一艘该型号飞艇第1次执行科考任务,能成功返航的概率为
科考任务,一艘该型号飞艇第1次执行科考任务,能成功返航的概率为 ,若第
,若第 次
次 执行科考任务能成功返航,则执行第
执行科考任务能成功返航,则执行第 次科考任务且能成功返航的概率也为
次科考任务且能成功返航的概率也为 ,否则此飞艇结束科考任务.一艘该型号飞艇每次执行科考任务,若能成功返航,则可获得价值为
,否则此飞艇结束科考任务.一艘该型号飞艇每次执行科考任务,若能成功返航,则可获得价值为 万元的科考数据,且“
万元的科考数据,且“ ”的概率为0.8,“
”的概率为0.8,“ ”的概率为0.2;若不能成功返航,则此次科考任务不能获得任何科考数据.记一艘该型号飞艇共可获得的科考数据的总价值为
”的概率为0.2;若不能成功返航,则此次科考任务不能获得任何科考数据.记一艘该型号飞艇共可获得的科考数据的总价值为 万元.
万元.(1)若
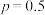 ,
, ,求
,求 的分布列;
的分布列;(2)求
 (用
(用 和
和 表示).
表示).
您最近一年使用:0次
2023-06-20更新
|
346次组卷
|
2卷引用:广东省阳江市2024届高三上学期开学适应性考试数学试题
名校
解题方法
8 . 已知椭圆 ,其右焦点为
,其右焦点为 ,以
,以 为端点作
为端点作 条射线交椭圆于
条射线交椭圆于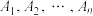 ,且每两条相邻射线的夹角相等,则( )
,且每两条相邻射线的夹角相等,则( )
 ,其右焦点为
,其右焦点为 ,以
,以 为端点作
为端点作 条射线交椭圆于
条射线交椭圆于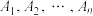 ,且每两条相邻射线的夹角相等,则( )
,且每两条相邻射线的夹角相等,则( )A.当 时, 时, |
B.当 时, 时,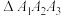 的面积的最小值为 的面积的最小值为 |
C.当 时, 时, |
D.当 时,过 时,过 作椭圆的切线 作椭圆的切线 ,且 ,且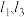 交于点 交于点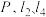 交于点 交于点 ,则 ,则 的斜率乘积为定值 的斜率乘积为定值 |
您最近一年使用:0次
2023-05-18更新
|
2234次组卷
|
6卷引用:广东省阳江市2024届高三上学期开学适应性考试数学试题
广东省阳江市2024届高三上学期开学适应性考试数学试题浙江省名校新高考研究联盟Z20联盟2023届高三第三次联考(三模)数学试题浙江省宁波市鄞州中学2023-2024学年高二上学期12月月考数学试题(已下线)专题12 椭圆-2(已下线)圆锥 曲线(已下线)压轴题02圆锥曲线压轴题17题型汇总-4
解题方法
9 . 已知正方体 的棱长为
的棱长为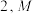 为空间中任一点,则下列结论中正确的是( )
为空间中任一点,则下列结论中正确的是( )
 的棱长为
的棱长为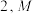 为空间中任一点,则下列结论中正确的是( )
为空间中任一点,则下列结论中正确的是( )A.若 为线段 为线段 上任一点,则 上任一点,则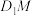 与 与 所成角的范围为 所成角的范围为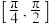 |
B.若 为正方形 为正方形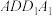 的中心,则三棱锥 的中心,则三棱锥 外接球的体积为 外接球的体积为 |
C.若 在正方形 在正方形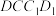 内部,且 内部,且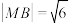 ,则点 ,则点 轨迹的长度为 轨迹的长度为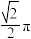 |
D.若三棱锥 的体积为 的体积为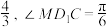 恒成立,点 恒成立,点 轨迹的为椭圆的一部分 轨迹的为椭圆的一部分 |
您最近一年使用:0次
2023-04-28更新
|
2645次组卷
|
6卷引用:广东省阳江市2024届高三上学期开学适应性考试数学试题
广东省阳江市2024届高三上学期开学适应性考试数学试题山东省济宁市2023届高三二模拟数学试题(已下线)模块九 第6套 1单选 2多选 2填空 2解答题(解析几何 导数)(已下线)模块六 专题2 易错题目重组卷(山东卷)福建省福州市鼓山中学2023届高三适应性练习数学试题(已下线)第八章立体几何初步(单元测试)-【上好课】-(人教A版2019必修第二册)
解题方法
10 . 2021年7月中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》,随后各学校积极响应,认真落实.“双减”不仅仅是减轻了学生家庭的经济负担、学生的课业负担,同时也增加了学生每天的体育锻炼时间.经过对某市义务教育阶段各学校学生平均每天体育锻炼时间的抽样调查,得出“双减”政策出台前(图1)与“双减”政策出台后(图2)的两个频率分布直方图.同一组中的数据用该组区间的中点值作代表,请解答下列问题:
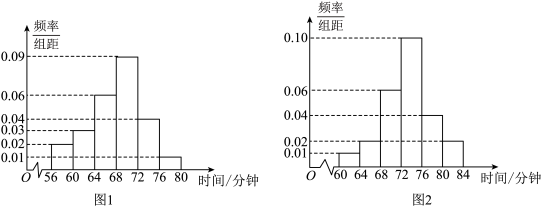
(1)根据上面两个频率分布直方图,估计“双减”政策出台后,学生平均每天的体育锻炼时间增加多少分钟;
(2)如果把每天平均体育锻炼时间在69分钟以上(含69分钟)的情况定义为“良”,把上述两个样本数据的频率视为概率,试估算出该市在“双减”政策出台后,学生平均每天的体育锻炼时间为“良”的概率.

(1)根据上面两个频率分布直方图,估计“双减”政策出台后,学生平均每天的体育锻炼时间增加多少分钟;
(2)如果把每天平均体育锻炼时间在69分钟以上(含69分钟)的情况定义为“良”,把上述两个样本数据的频率视为概率,试估算出该市在“双减”政策出台后,学生平均每天的体育锻炼时间为“良”的概率.
您最近一年使用:0次
2023-04-25更新
|
539次组卷
|
3卷引用:广东省阳江市2023-2024学年高二上学期期中数学试题



