解题方法
1 . 已知函数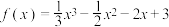 ,
,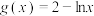 .
.
(1)求函数 的极值;
的极值;
(2)曲线 在
在 处的切线方程为
处的切线方程为 ,证明:
,证明: .
.
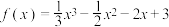 ,
,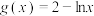 .
.(1)求函数
 的极值;
的极值;(2)曲线
 在
在 处的切线方程为
处的切线方程为 ,证明:
,证明: .
.
您最近一年使用:0次
2024-07-04更新
|
723次组卷
|
3卷引用:湖南省部分学校2025届新高三联合教学质量检测数学试题
2 . 已知函数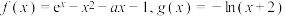 .
.
(1)若 是
是 的极大值点,求
的极大值点,求 的值;
的值;
(2)用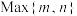 表示
表示 中的最大值,设函数
中的最大值,设函数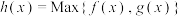 ,试讨论
,试讨论 零点的个数.
零点的个数.
注:若 ,当
,当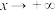 时,
时, ,当
,当 时,
时,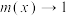 .
.
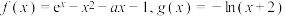 .
.(1)若
 是
是 的极大值点,求
的极大值点,求 的值;
的值;(2)用
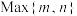 表示
表示 中的最大值,设函数
中的最大值,设函数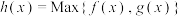 ,试讨论
,试讨论 零点的个数.
零点的个数.注:若
 ,当
,当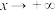 时,
时, ,当
,当 时,
时,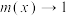 .
.
您最近一年使用:0次
3 . 在锐角 中,
中, 依次为三个内角
依次为三个内角 的对边,已知
的对边,已知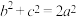 ,求
,求 的取值范围为
的取值范围为______ .
 中,
中, 依次为三个内角
依次为三个内角 的对边,已知
的对边,已知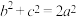 ,求
,求 的取值范围为
的取值范围为
您最近一年使用:0次
名校
解题方法
4 . 定义在 上的函数
上的函数 与
与 的导函数分别为
的导函数分别为 和
和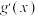 ,若
,若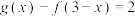 ,
,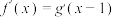 ,且
,且 ,则下列说法中一定不正确的是( )
,则下列说法中一定不正确的是( )
 上的函数
上的函数 与
与 的导函数分别为
的导函数分别为 和
和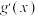 ,若
,若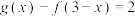 ,
,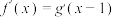 ,且
,且 ,则下列说法中一定不正确的是( )
,则下列说法中一定不正确的是( )A. 为偶函数 为偶函数 | B.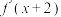 为奇函数 为奇函数 |
C.函数 是周期函数 是周期函数 | D.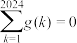 |
您最近一年使用:0次
2024-09-24更新
|
300次组卷
|
2卷引用:湖南省长沙市长郡梅溪湖中学2023-2024学年高二下学期期中考试数学试卷
名校
5 . 已知函数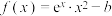 有三个零点,则
有三个零点,则 的取值范围是( )
的取值范围是( )
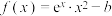 有三个零点,则
有三个零点,则 的取值范围是( )
的取值范围是( )A.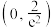 | B.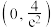 |
C.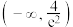 | D.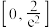 |
您最近一年使用:0次
2024-09-04更新
|
1187次组卷
|
3卷引用:湖南省岳阳市第一中学2025届高三下学期第二次检测数学试题
解题方法
6 . 已知函数 的导函数是
的导函数是 ,且
,且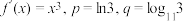 ,则下列命题正确的是( )
,则下列命题正确的是( )
 的导函数是
的导函数是 ,且
,且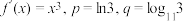 ,则下列命题正确的是( )
,则下列命题正确的是( )A.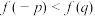 | B.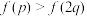 |
C.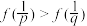 | D.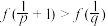 |
您最近一年使用:0次
名校
解题方法
7 . 已知定义在 上的函数
上的函数 满足
满足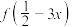 为偶函数,
为偶函数,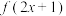 为奇函数,当
为奇函数,当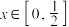 时,
时,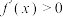 ,则下列说法正确的是( )
,则下列说法正确的是( )
 上的函数
上的函数 满足
满足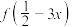 为偶函数,
为偶函数,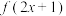 为奇函数,当
为奇函数,当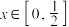 时,
时,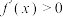 ,则下列说法正确的是( )
,则下列说法正确的是( )A. | B.函数 为周期函数 为周期函数 |
C.函数 为 为 上的偶函数 上的偶函数 | D.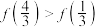 |
您最近一年使用:0次
2024-09-03更新
|
1955次组卷
|
5卷引用:湖南省2024届高三仿真模拟考试(五)数学试题
24-25高三上·广东深圳·开学考试
名校
8 . 对勾函数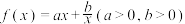 的图象可以由焦点在坐标轴上的双曲线绕原点旋转得到,因此对勾函数即为双曲线.已知O为坐标原点,下列关于函数
的图象可以由焦点在坐标轴上的双曲线绕原点旋转得到,因此对勾函数即为双曲线.已知O为坐标原点,下列关于函数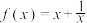 的说法正确的是( )
的说法正确的是( )
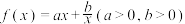 的图象可以由焦点在坐标轴上的双曲线绕原点旋转得到,因此对勾函数即为双曲线.已知O为坐标原点,下列关于函数
的图象可以由焦点在坐标轴上的双曲线绕原点旋转得到,因此对勾函数即为双曲线.已知O为坐标原点,下列关于函数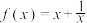 的说法正确的是( )
的说法正确的是( )A.渐近线方程为 和 和 |
B. 的对称轴方程为 的对称轴方程为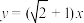 和 和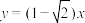 |
C.M,N是函数 图象上两动点,P为MN的中点,则直线MN,OP的斜率之积为定值 图象上两动点,P为MN的中点,则直线MN,OP的斜率之积为定值 |
D.Q是函数 图象上任意一点,过点Q作切线交渐近线于A,B两点,则 图象上任意一点,过点Q作切线交渐近线于A,B两点,则 的面积为定值 的面积为定值 |
您最近一年使用:0次
9 . 已知函数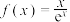 ,
,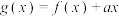 .
.
(1)若 在
在 处取得极值,讨论
处取得极值,讨论 的单调性;
的单调性;
(2)设曲线 在点
在点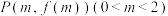 处的切线为
处的切线为 ,证明:除点
,证明:除点 外,曲线段
外,曲线段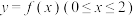 总在
总在 的下方;
的下方;
(3)设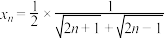 ,证明:
,证明: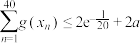 .
.
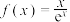 ,
,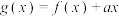 .
.(1)若
 在
在 处取得极值,讨论
处取得极值,讨论 的单调性;
的单调性;(2)设曲线
 在点
在点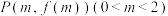 处的切线为
处的切线为 ,证明:除点
,证明:除点 外,曲线段
外,曲线段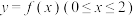 总在
总在 的下方;
的下方;(3)设
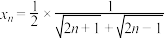 ,证明:
,证明: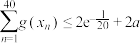 .
.
您最近一年使用:0次
10 . 已知函数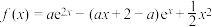 .
.
(1)讨论 的单调性;
的单调性;
(2)若 有两个零点,求a的取值范围.
有两个零点,求a的取值范围.
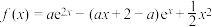 .
.(1)讨论
 的单调性;
的单调性;(2)若
 有两个零点,求a的取值范围.
有两个零点,求a的取值范围.
您最近一年使用:0次



