名校
1 . 在几何学常常需要考虑曲线的弯曲程度,为此我们需要刻画曲线的弯曲程度.考察如图所示的光滑曲线C: 上的曲线段
上的曲线段 ,其弧长为
,其弧长为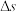 ,当动点从A沿曲线段
,当动点从A沿曲线段 运动到B点时,A点的切线
运动到B点时,A点的切线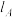 也随着转动到B点的切线
也随着转动到B点的切线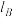 ,记这两条切线之间的夹角为
,记这两条切线之间的夹角为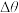 (它等于
(它等于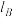 的倾斜角与
的倾斜角与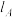 的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义
的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义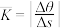 为曲线段
为曲线段 的平均曲率;显然当B越接近A,即
的平均曲率;显然当B越接近A,即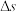 越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义
越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义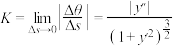 (若极限存在)为曲线C在点A处的曲率.(其中y',y''分别表示
(若极限存在)为曲线C在点A处的曲率.(其中y',y''分别表示 在点A处的一阶、二阶导数)
在点A处的一阶、二阶导数)
(2)求椭圆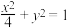 在
在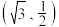 处的曲率;
处的曲率;
(3)定义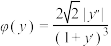 为曲线
为曲线 的“柯西曲率”.已知在曲线
的“柯西曲率”.已知在曲线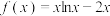 上存在两点
上存在两点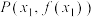 和
和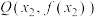 ,且P,Q处的“柯西曲率”相同,求
,且P,Q处的“柯西曲率”相同,求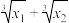 的取值范围.
的取值范围.
 上的曲线段
上的曲线段 ,其弧长为
,其弧长为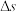 ,当动点从A沿曲线段
,当动点从A沿曲线段 运动到B点时,A点的切线
运动到B点时,A点的切线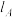 也随着转动到B点的切线
也随着转动到B点的切线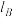 ,记这两条切线之间的夹角为
,记这两条切线之间的夹角为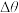 (它等于
(它等于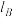 的倾斜角与
的倾斜角与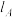 的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义
的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义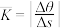 为曲线段
为曲线段 的平均曲率;显然当B越接近A,即
的平均曲率;显然当B越接近A,即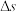 越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义
越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义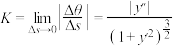 (若极限存在)为曲线C在点A处的曲率.(其中y',y''分别表示
(若极限存在)为曲线C在点A处的曲率.(其中y',y''分别表示 在点A处的一阶、二阶导数)
在点A处的一阶、二阶导数)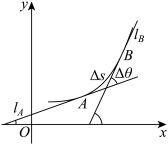
(2)求椭圆
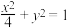 在
在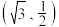 处的曲率;
处的曲率;(3)定义
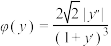 为曲线
为曲线 的“柯西曲率”.已知在曲线
的“柯西曲率”.已知在曲线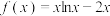 上存在两点
上存在两点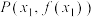 和
和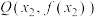 ,且P,Q处的“柯西曲率”相同,求
,且P,Q处的“柯西曲率”相同,求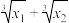 的取值范围.
的取值范围.
您最近一年使用:0次
2024-01-29更新
|
3090次组卷
|
8卷引用:浙江省宁波市镇海中学2024届高三上学期期末数学试题
浙江省宁波市镇海中学2024届高三上学期期末数学试题湖北省武汉市武钢三中2024届高三下学期开学考试数学试题(已下线)第四套 九省联考全真模拟(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)新题型01 新高考新结构二十一大考点汇总-3(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编湖南省长沙外国语学校2023-2024学年高二下学期3月月考数学试题山东省菏泽市定陶区第一中学2023-2024学年高二下学期第一次月考数学试题
名校
解题方法
2 . 悬链线的原理运用于悬索桥、架空电缆、双曲拱桥、拱坝等工程.通过适当建立坐标系,悬链线可为双曲余弦函数 的图象,类比三角函数的三种性质:①平方关系:①
的图象,类比三角函数的三种性质:①平方关系:①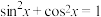 ,②和角公式:
,②和角公式: ,③导数:
,③导数: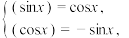 定义双曲正弦函数
定义双曲正弦函数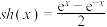 .
.
(1)直接写出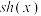 ,
,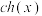 具有的类似①、②、③的三种性质(不需要证明);
具有的类似①、②、③的三种性质(不需要证明);
(2)若当 时,
时, 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)求 的最小值.
的最小值.
 的图象,类比三角函数的三种性质:①平方关系:①
的图象,类比三角函数的三种性质:①平方关系:①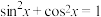 ,②和角公式:
,②和角公式: ,③导数:
,③导数: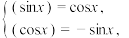 定义双曲正弦函数
定义双曲正弦函数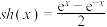 .
.(1)直接写出
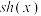 ,
,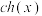 具有的类似①、②、③的三种性质(不需要证明);
具有的类似①、②、③的三种性质(不需要证明);(2)若当
 时,
时, 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(3)求
 的最小值.
的最小值.
您最近一年使用:0次
2024-01-27更新
|
2025次组卷
|
7卷引用:浙江省湖州市第一中学2024届高三下学期新高考数学模拟试题
浙江省湖州市第一中学2024届高三下学期新高考数学模拟试题云南省昆明市第一中学2024届高三上学期第六次考前基础强化数学试题2024届高三新改革适应性模拟测试数学试卷一(九省联考题型)(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编江苏省常州高级中学2023-2024学年高二下学期第一次调研考试数学试题2024届山西省平遥县第二中学校高三冲刺调研押题卷数学(二)
名校
解题方法
3 . 学习强国中有两项竞赛答题活动,一项为“双人对战”,另一项为“四人赛”.活动规则如下:一天内参与“双人对战”活动,仅首局比赛可获得积分,获胜得2分,失败得1分;一天内参与“四人赛”活动,仅前两局比赛可获得积分,首局获胜得3分,次局获胜得2分,失败均得1分.已知李明参加“双人对战”活动时,每局比赛获胜的概率为 ;参加“四人赛”活动(每天两局)时,第一局和第二局比赛获胜的概率分别为p,
;参加“四人赛”活动(每天两局)时,第一局和第二局比赛获胜的概率分别为p, .李明周一到周五每天都参加了“双人对战”活动和“四人赛”活动(每天两局),各局比赛互不影响.
.李明周一到周五每天都参加了“双人对战”活动和“四人赛”活动(每天两局),各局比赛互不影响.
(1)求李明这5天参加“双人对战”活动的总得分X的分布列和数学期望;
(2)设李明在这5天的“四人赛”活动(每天两局)中,恰有3天每天得分不低于3分的概率为 .求p为何值时,
.求p为何值时, 取得最大值.
取得最大值.
 ;参加“四人赛”活动(每天两局)时,第一局和第二局比赛获胜的概率分别为p,
;参加“四人赛”活动(每天两局)时,第一局和第二局比赛获胜的概率分别为p, .李明周一到周五每天都参加了“双人对战”活动和“四人赛”活动(每天两局),各局比赛互不影响.
.李明周一到周五每天都参加了“双人对战”活动和“四人赛”活动(每天两局),各局比赛互不影响.(1)求李明这5天参加“双人对战”活动的总得分X的分布列和数学期望;
(2)设李明在这5天的“四人赛”活动(每天两局)中,恰有3天每天得分不低于3分的概率为
 .求p为何值时,
.求p为何值时, 取得最大值.
取得最大值.
您最近一年使用:0次
2022-01-22更新
|
3972次组卷
|
13卷引用:浙江省杭嘉湖金四县区2022-2023学年高二下学期5月调研测试数学试题
浙江省杭嘉湖金四县区2022-2023学年高二下学期5月调研测试数学试题山东省淄博市2021-2022学年高三上学期期末数学试题山东省威海市2021-2022学年高三上学期期末数学试题广东省名校2022届高三下学期开学考试数学试题江西省新余市2022届高三第二次模拟考试数学(理)试题福建省莆田华侨中学2022届高三下学期模拟考试数学试题2023版 湘教版(2019) 选修第二册 过关斩将 第3章 本章复习提升沪教版(2020) 选修第二册 经典学案 第7章 单元测试(已下线)山东省威海市2022-2023学年高三上学期12月联考数学试题(已下线)专题9-1 概率与统计及分布列归类(理)(讲+练)-2(已下线)第7章 概率初步(续)【单元提升卷】-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)(已下线)第九章 重难专攻(十二)概率中的综合题 (讲)一轮点点通(已下线)微考点7-1 分布列概率中的三大最值问题(三大题型)
名校
解题方法
4 . 2023年10月5日晚,杭州亚运会女篮决赛的巅峰对决中,中国女篮以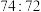 战胜日本女篮,成功卫冕亚运会冠军,大快人心,表现神勇,为国家和人民争了光.某校随即开展了“学习女篮精神,塑造健康体魄”的主题活动,在该活动的某次篮球训练课上,进行了一场
战胜日本女篮,成功卫冕亚运会冠军,大快人心,表现神勇,为国家和人民争了光.某校随即开展了“学习女篮精神,塑造健康体魄”的主题活动,在该活动的某次篮球训练课上,进行了一场 、
、 、
、 3名女篮队员的传接球的训练,球从
3名女篮队员的传接球的训练,球从 手中开始,等可能地随机传向另外2人中的1人,接球者接到球后再等可能地随机传向另外2人中的1人,如此不停地传下去,假设传出的球都能被接住.记第
手中开始,等可能地随机传向另外2人中的1人,接球者接到球后再等可能地随机传向另外2人中的1人,如此不停地传下去,假设传出的球都能被接住.记第 次传球之前球在
次传球之前球在 手中的概率为
手中的概率为 ,易知
,易知 ,
, .
.
(1)①求第5次传球前,球恰好在 手中的概率
手中的概率 ;
;
②第 次传球前球在
次传球前球在 手中的概率为
手中的概率为 ,试比较
,试比较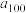 与
与 的大小.
的大小.
(2)训练结束,体育老师为了表扬队员们精彩的表现和取得的进步,组织了一场“摸球抽奖”活动,先在一个口袋中装有 个红球(
个红球( 且
且 )和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.若设三次摸奖(每次摸奖后球放回)恰好有一次中奖的概率
)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.若设三次摸奖(每次摸奖后球放回)恰好有一次中奖的概率 ,当
,当 取何值时,
取何值时, 最大?
最大?
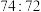 战胜日本女篮,成功卫冕亚运会冠军,大快人心,表现神勇,为国家和人民争了光.某校随即开展了“学习女篮精神,塑造健康体魄”的主题活动,在该活动的某次篮球训练课上,进行了一场
战胜日本女篮,成功卫冕亚运会冠军,大快人心,表现神勇,为国家和人民争了光.某校随即开展了“学习女篮精神,塑造健康体魄”的主题活动,在该活动的某次篮球训练课上,进行了一场 、
、 、
、 3名女篮队员的传接球的训练,球从
3名女篮队员的传接球的训练,球从 手中开始,等可能地随机传向另外2人中的1人,接球者接到球后再等可能地随机传向另外2人中的1人,如此不停地传下去,假设传出的球都能被接住.记第
手中开始,等可能地随机传向另外2人中的1人,接球者接到球后再等可能地随机传向另外2人中的1人,如此不停地传下去,假设传出的球都能被接住.记第 次传球之前球在
次传球之前球在 手中的概率为
手中的概率为 ,易知
,易知 ,
, .
.(1)①求第5次传球前,球恰好在
 手中的概率
手中的概率 ;
;②第
 次传球前球在
次传球前球在 手中的概率为
手中的概率为 ,试比较
,试比较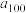 与
与 的大小.
的大小.(2)训练结束,体育老师为了表扬队员们精彩的表现和取得的进步,组织了一场“摸球抽奖”活动,先在一个口袋中装有
 个红球(
个红球( 且
且 )和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.若设三次摸奖(每次摸奖后球放回)恰好有一次中奖的概率
)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.若设三次摸奖(每次摸奖后球放回)恰好有一次中奖的概率 ,当
,当 取何值时,
取何值时, 最大?
最大?
您最近一年使用:0次
2023-11-09更新
|
1607次组卷
|
5卷引用:浙江省宁波市北仑中学2023-2024学年高二下学期期中考试数学试题
浙江省宁波市北仑中学2023-2024学年高二下学期期中考试数学试题湖北省部分重点中学2024届高三上学期第一次联考数学试题江苏省南京市金陵中学2024届高三上学期期末模拟数学试题(已下线)第4讲:概率与数列的结合问题【练】(已下线)【一题多变】传球问题 构造数列
名校
5 . 已知 是方程
是方程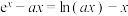 的两个实根,且
的两个实根,且 .
.
(1)求实数 的取值范围;
的取值范围;
(2)已知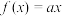 ,
,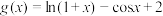 ,若存在正实数
,若存在正实数 ,使得
,使得 成立,证明:
成立,证明: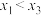 .
.
 是方程
是方程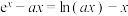 的两个实根,且
的两个实根,且 .
.(1)求实数
 的取值范围;
的取值范围;(2)已知
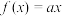 ,
,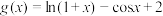 ,若存在正实数
,若存在正实数 ,使得
,使得 成立,证明:
成立,证明: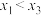 .
.
您最近一年使用:0次
2023-05-26更新
|
1398次组卷
|
6卷引用:浙江省杭州第二中学等四校2023届高三下学期5月高考模拟数学试题
浙江省杭州第二中学等四校2023届高三下学期5月高考模拟数学试题 2023届浙江省四校联盟高三下学期数学模拟试卷湖南省长沙市第一中学2022-2023学年高二下学期第三次阶段性测试数学试题重庆市万州第二高级中学2024届高三上学期8月月考数学试题(已下线)第九章 导数与三角函数的联袂 专题三 含三角函数的恒成立问题 微点3 三角函数的恒成立问题(三)(已下线)专题19 导数综合-2
6 . 已知函数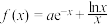 .
.
(1)若 是
是 的极值点,求a;
的极值点,求a;
(2)若 ,
, 分别是
分别是 的零点和极值点,证明下面①,②中的一个.
的零点和极值点,证明下面①,②中的一个.
①当 时,
时,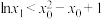 ;②当
;②当 时,
时,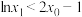 .
.
注:如果选择①,②分别解答,则按第一个解答计分.
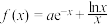 .
.(1)若
 是
是 的极值点,求a;
的极值点,求a;(2)若
 ,
, 分别是
分别是 的零点和极值点,证明下面①,②中的一个.
的零点和极值点,证明下面①,②中的一个.①当
 时,
时,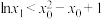 ;②当
;②当 时,
时,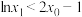 .
.注:如果选择①,②分别解答,则按第一个解答计分.
您最近一年使用:0次
2022-12-26更新
|
2052次组卷
|
7卷引用:2022年9月《浙江省新高考研究卷》(全国I卷)数学试题(五)
2022年9月《浙江省新高考研究卷》(全国I卷)数学试题(五)湖南省株洲市二中教育集团2023届高三上学期1月期末联考数学试题(已下线)技巧04 结构不良问题解题策略(精讲精练)-1(已下线)专题4 劣构题题型(已下线)高考新题型-一元函数的导数及其应用重庆市万州第二高级中学2023届高三三诊数学试题(已下线)技巧04 结构不良问题解题策略(5大题型)(练习)
解题方法
7 . 某公司生产一种大件产品的日产为2件,每件产品质量为一等的概率为0.5,二等的概率为0.4,若达不到一、二级,则为不合格,且生产两件产品品质结果相互独立.已知生产一件产品的利润如下表:
(1)求生产两件产品中至少有一件一等品的概率;
(2)求该公司每天所获利润 (万元)的数学期望;
(万元)的数学期望;
(3)若该工厂要增加日产能,公司工厂需引入设备及更新技术,但增加n件产能,其成本也将相应提升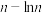 (万元),假如你作为工厂决策者,你觉得该厂目前该不该增产?请回答,并说明理由.(
(万元),假如你作为工厂决策者,你觉得该厂目前该不该增产?请回答,并说明理由.( )
)
等级 | 一等 | 二等 | 三等 |
利润(万元/每件) | 0.8 | 0.6 | -0.3 |
(2)求该公司每天所获利润
 (万元)的数学期望;
(万元)的数学期望;(3)若该工厂要增加日产能,公司工厂需引入设备及更新技术,但增加n件产能,其成本也将相应提升
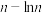 (万元),假如你作为工厂决策者,你觉得该厂目前该不该增产?请回答,并说明理由.(
(万元),假如你作为工厂决策者,你觉得该厂目前该不该增产?请回答,并说明理由.( )
)
您最近一年使用:0次
2023-05-12更新
|
957次组卷
|
4卷引用:浙江省金丽衢十二校2023届高三下学期第二次联考数学试题
浙江省金丽衢十二校2023届高三下学期第二次联考数学试题山东省东营市2022-2023学年高二下学期期末数学试题【人教A版(2019)】专题15概率与统计(第五部分)-高二下学期名校期末好题汇编(已下线)重组1 高二期末真题重组卷(山东卷)B提升卷
解题方法
8 . 已知函数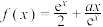 .
.
(1)当 时,记函数
时,记函数 的导数为
的导数为 ,求
,求 的值.
的值.
(2)当 ,
, 时,证明:
时,证明: .
.
(3)当 时,令
时,令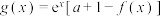 ,
, 的图象在
的图象在 ,
, 处切线的斜率相同,记
处切线的斜率相同,记 的最小值为
的最小值为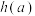 ,求
,求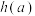 的最小值.
的最小值.
(注: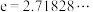 是自然对数的底数).
是自然对数的底数).
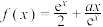 .
.(1)当
 时,记函数
时,记函数 的导数为
的导数为 ,求
,求 的值.
的值.(2)当
 ,
, 时,证明:
时,证明: .
.(3)当
 时,令
时,令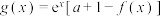 ,
, 的图象在
的图象在 ,
, 处切线的斜率相同,记
处切线的斜率相同,记 的最小值为
的最小值为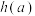 ,求
,求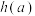 的最小值.
的最小值.(注:
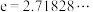 是自然对数的底数).
是自然对数的底数).
您最近一年使用:0次
名校
9 . 设全集为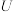 ,定义域为
,定义域为 的函数
的函数 是关于x的函数“函数组”,当n取
是关于x的函数“函数组”,当n取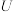 中不同的数值时可以得到不同的函数.例如:定义域为
中不同的数值时可以得到不同的函数.例如:定义域为 的函数
的函数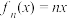 ,当
,当 时,有
时,有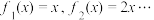 若存在非空集合
若存在非空集合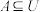 满足当且仅当
满足当且仅当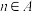 时,函数
时,函数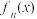 在
在 上存在零点,则称
上存在零点,则称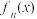 是
是 上的“跳跃函数”.
上的“跳跃函数”.
(1)设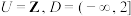 ,若函数
,若函数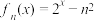 是
是 上的“跳跃函数”,求集合
上的“跳跃函数”,求集合 ;
;
(2)设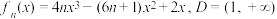 ,若不存在集合
,若不存在集合 使
使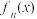 为
为 上的“跳跃函数”,求所有满足条件的集合
上的“跳跃函数”,求所有满足条件的集合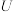 的并集;
的并集;
(3)设 ,
,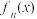 为
为 上的“跳跃函数”,
上的“跳跃函数”,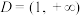 .已知
.已知 ,且对任意正整数n,均有
,且对任意正整数n,均有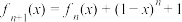 .
.
(i)证明: ;
;
(ii)求实数 的最大值,使得对于任意
的最大值,使得对于任意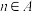 ,均有
,均有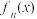 的零点
的零点 .
.
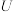 ,定义域为
,定义域为 的函数
的函数 是关于x的函数“函数组”,当n取
是关于x的函数“函数组”,当n取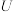 中不同的数值时可以得到不同的函数.例如:定义域为
中不同的数值时可以得到不同的函数.例如:定义域为 的函数
的函数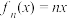 ,当
,当 时,有
时,有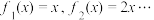 若存在非空集合
若存在非空集合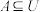 满足当且仅当
满足当且仅当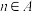 时,函数
时,函数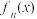 在
在 上存在零点,则称
上存在零点,则称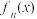 是
是 上的“跳跃函数”.
上的“跳跃函数”.(1)设
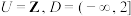 ,若函数
,若函数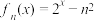 是
是 上的“跳跃函数”,求集合
上的“跳跃函数”,求集合 ;
;(2)设
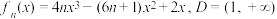 ,若不存在集合
,若不存在集合 使
使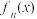 为
为 上的“跳跃函数”,求所有满足条件的集合
上的“跳跃函数”,求所有满足条件的集合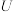 的并集;
的并集;(3)设
 ,
,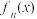 为
为 上的“跳跃函数”,
上的“跳跃函数”,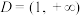 .已知
.已知 ,且对任意正整数n,均有
,且对任意正整数n,均有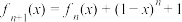 .
.(i)证明:
 ;
;(ii)求实数
 的最大值,使得对于任意
的最大值,使得对于任意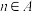 ,均有
,均有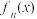 的零点
的零点 .
.
您最近一年使用:0次
名校
解题方法
10 . 已知 ,
,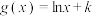 ,
,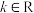 .
.
(1)若 恒成立,证明:
恒成立,证明: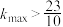 ;
;
(2)对于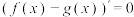 有
有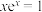 ,其根可设为
,其根可设为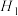 ,相同地,对于
,相同地,对于 ,其根可设为
,其根可设为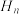 ,令
,令 .
.
(i)证明: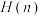 在
在 上单调递增;
上单调递增;
(ii)若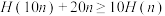 ,求n的取值范围.
,求n的取值范围.
 ,
,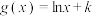 ,
,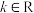 .
.(1)若
 恒成立,证明:
恒成立,证明: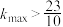 ;
;(2)对于
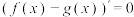 有
有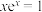 ,其根可设为
,其根可设为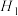 ,相同地,对于
,相同地,对于 ,其根可设为
,其根可设为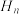 ,令
,令 .
.(i)证明:
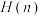 在
在 上单调递增;
上单调递增;(ii)若
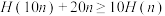 ,求n的取值范围.
,求n的取值范围.
您最近一年使用:0次



