解题方法
1 . 已知函数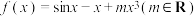 .
.
(1)当 时,证明:
时,证明: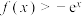 ;
;
(2)已知 ,
,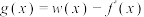 ,求证:函数
,求证:函数 存在极小值.
存在极小值.
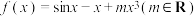 .
.(1)当
 时,证明:
时,证明: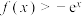 ;
;(2)已知
 ,
,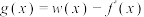 ,求证:函数
,求证:函数 存在极小值.
存在极小值.
您最近一年使用:0次
2 . 固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程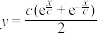 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数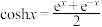 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数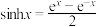 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.
(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论: _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);
(2)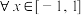 ,不等式
,不等式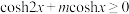 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若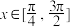 ,试比较
,试比较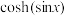 与
与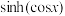 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
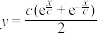 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数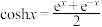 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数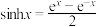 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论:
 _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);(2)
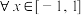 ,不等式
,不等式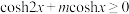 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
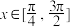 ,试比较
,试比较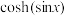 与
与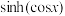 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
您最近一年使用:0次
2024-01-27更新
|
959次组卷
|
11卷引用:江西省上饶市横峰县横峰中学2023-2024学年高一下学期期中考试数学试卷
江西省上饶市横峰县横峰中学2023-2024学年高一下学期期中考试数学试卷福建省宁德市2023-2024学年高一上学期1月期末质量检测数学试题重庆市缙云教育联盟2024届高三下学期2月月度质量检测数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)讲河南省名校联盟2023-2024学年高一下学期3月测试数学试题(已下线)第八章:向量的数量积与三角恒等变换章末重点题型复习(2)-同步精品课堂(人教B版2019必修第三册)河南省信阳市信阳高级中学2023-2024学年高一下学期3月月考(一)数学试题(已下线)第8章:向量的数量积与三角恒等变换章末综合检测卷(新题型)-【帮课堂】(人教B版2019必修第三册)(已下线)专题04 三角函数恒等变形综合大题归类 -期末考点大串讲(苏教版(2019))(已下线)专题08 期末必刷解答题专题训练的7种常考题型归类-期末真题分类汇编(北师大版2019必修第二册)(已下线)拔高点突破05 函数与导数背景下的新定义压轴解答题(九大题型)
名校
3 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.
例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵ ,∴
,∴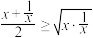 ,即
,即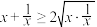 ,∴
,∴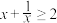 ,
,
当且仅当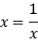 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)已知如 ,求下列各式的值:
,求下列各式的值:
①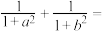 ___________.
___________.
②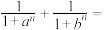 ___________.
___________.
(2)若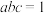 ,解方程
,解方程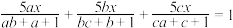 .
.
(3)若正数a、b满足 ,求
,求 的最小值.
的最小值.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式
 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.例如:在
 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵
 ,∴
,∴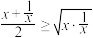 ,即
,即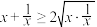 ,∴
,∴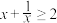 ,
,当且仅当
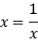 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)已知如
 ,求下列各式的值:
,求下列各式的值:①
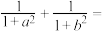 ___________.
___________.②
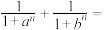 ___________.
___________.(2)若
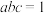 ,解方程
,解方程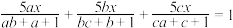 .
.(3)若正数a、b满足
 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2021-10-29更新
|
532次组卷
|
3卷引用:江西省南昌市第二中学2023-2024学年高一上学期月考数学试题(一)
江西省南昌市第二中学2023-2024学年高一上学期月考数学试题(一)江苏省南通中学2020-2021学年高一上学期开学考试数学试题(已下线)第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)
名校
解题方法
4 . 如图1,在等腰梯形 中,
中, ,
, ,
,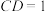 ,
, ,E、F分别为腰
,E、F分别为腰 、
、 的中点.将四边形
的中点.将四边形 沿
沿 折起,使平面
折起,使平面 平面
平面 ,如图2,H,M别线段
,如图2,H,M别线段 、
、 的中点.
的中点.
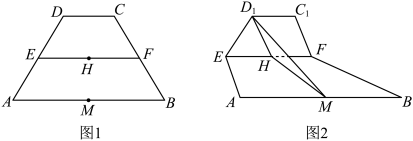
(1)求证: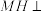 平面
平面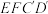 ;
;
(2)请在图2所给的点中找出两个点,使得这两点所在直线与平面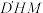 垂直,并给出证明:
垂直,并给出证明:
(3)若N为线段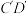 中点,在直线
中点,在直线 上是否存在点Q,使得
上是否存在点Q,使得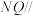 面
面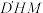 ?如果存在,求出线段
?如果存在,求出线段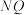 的长度,如果不存在,请说明理由.
的长度,如果不存在,请说明理由.
 中,
中, ,
, ,
,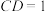 ,
, ,E、F分别为腰
,E、F分别为腰 、
、 的中点.将四边形
的中点.将四边形 沿
沿 折起,使平面
折起,使平面 平面
平面 ,如图2,H,M别线段
,如图2,H,M别线段 、
、 的中点.
的中点.
(1)求证:
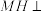 平面
平面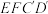 ;
;(2)请在图2所给的点中找出两个点,使得这两点所在直线与平面
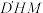 垂直,并给出证明:
垂直,并给出证明:(3)若N为线段
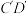 中点,在直线
中点,在直线 上是否存在点Q,使得
上是否存在点Q,使得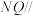 面
面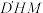 ?如果存在,求出线段
?如果存在,求出线段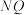 的长度,如果不存在,请说明理由.
的长度,如果不存在,请说明理由.
您最近一年使用:0次
2020-11-02更新
|
1360次组卷
|
4卷引用:江西省抚州市黎川县第一中学2020-2021学年高一下学期期末数学(理)试题
名校
解题方法
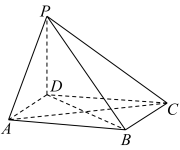
5 . 如图,在四棱锥 中,
中,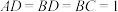 ,
,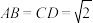 ,
, ,平面
,平面 平面ABCD.
平面ABCD.
(1)求证: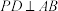 ;
;
(2)已知二面角 的余弦值为
的余弦值为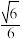 .线段PC上是否存在点M,使得BM与平面PAC所成的角为30°?证明你的结论.
.线段PC上是否存在点M,使得BM与平面PAC所成的角为30°?证明你的结论.
 中,
中,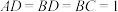 ,
,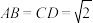 ,
, ,平面
,平面 平面ABCD.
平面ABCD.
(1)求证:
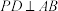 ;
;(2)已知二面角
 的余弦值为
的余弦值为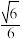 .线段PC上是否存在点M,使得BM与平面PAC所成的角为30°?证明你的结论.
.线段PC上是否存在点M,使得BM与平面PAC所成的角为30°?证明你的结论.
您最近一年使用:0次
2021-01-13更新
|
977次组卷
|
5卷引用:江西省分宜中学2020-2021学年高二下学期第一次段考数学(理)试题
名校
6 . 已知 ,其中
,其中 为常数.
为常数.
(1)当 时,求证:不等式
时,求证:不等式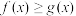 恒成立;
恒成立;
(2)当 时,记方程
时,记方程 的两根为
的两根为 和
和 ,试判断
,试判断 与
与 的大小,并证明.
的大小,并证明.
 ,其中
,其中 为常数.
为常数.(1)当
 时,求证:不等式
时,求证:不等式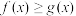 恒成立;
恒成立;(2)当
 时,记方程
时,记方程 的两根为
的两根为 和
和 ,试判断
,试判断 与
与 的大小,并证明.
的大小,并证明.
您最近一年使用:0次
名校
7 . 完成下列证明:
(Ⅰ)求证: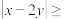
 ;
;
(Ⅱ)若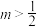 ,求证:
,求证: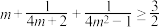 .
.
(Ⅰ)求证:
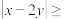
 ;
;(Ⅱ)若
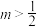 ,求证:
,求证: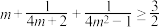 .
.
您最近一年使用:0次
2019-09-12更新
|
1116次组卷
|
3卷引用:江西省吉安市2018-2019学年高二下学期期末数学(理)试题
名校
8 . 已知定义在 上的函数
上的函数 满足以下三个条件:
满足以下三个条件:
①对任意实数 ,都有
,都有 ;
;
②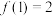 ;
;
③ 在区间
在区间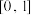 上为增函数.
上为增函数.
(1)判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)求证: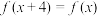 ;
;
(3)解不等式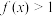 .
.
 上的函数
上的函数 满足以下三个条件:
满足以下三个条件:①对任意实数
 ,都有
,都有 ;
;②
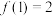 ;
;③
 在区间
在区间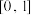 上为增函数.
上为增函数.(1)判断函数
 的奇偶性,并加以证明;
的奇偶性,并加以证明;(2)求证:
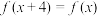 ;
;(3)解不等式
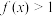 .
.
您最近一年使用:0次
2019-12-01更新
|
930次组卷
|
3卷引用:江西省宜春市丰城中学2023-2024学年高一下学期开学考试数学试题
名校
9 . 已知定义在 上的函数
上的函数 满足:对任意
满足:对任意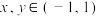 都有
都有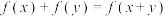 .
.
(1)求证:函数 是奇函数;
是奇函数;
(2)如果当 时,有
时,有 ,试判断
,试判断 在
在 上的单调性,并用定义证明你的判断;
上的单调性,并用定义证明你的判断;
(3)在(2)的条件下,若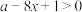 对满足不等式
对满足不等式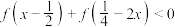 的任意
的任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 上的函数
上的函数 满足:对任意
满足:对任意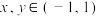 都有
都有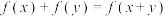 .
.(1)求证:函数
 是奇函数;
是奇函数;(2)如果当
 时,有
时,有 ,试判断
,试判断 在
在 上的单调性,并用定义证明你的判断;
上的单调性,并用定义证明你的判断;(3)在(2)的条件下,若
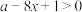 对满足不等式
对满足不等式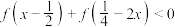 的任意
的任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2019-10-26更新
|
676次组卷
|
3卷引用:江西省抚州市南城县第二中学2019-2020学年高一上学期第一次月考数学试题
名校
10 . 已知函数 ,其中
,其中 .
.
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)当 时,证明:
时,证明: ;
;
(Ⅲ)求证:对任意正整数n,都有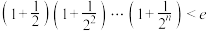 (其中e≈2.7183为自然对数的底数)
(其中e≈2.7183为自然对数的底数)
 ,其中
,其中 .
.(Ⅰ)讨论
 的单调性;
的单调性;(Ⅱ)当
 时,证明:
时,证明: ;
;(Ⅲ)求证:对任意正整数n,都有
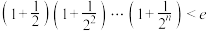 (其中e≈2.7183为自然对数的底数)
(其中e≈2.7183为自然对数的底数)
您最近一年使用:0次
2019-01-12更新
|
4102次组卷
|
10卷引用:江西省五市八校2019-2020学年高三第二次联考文科数学试题
江西省五市八校2019-2020学年高三第二次联考文科数学试题【区级联考】天津市蓟州等部分区2019届高三上学期期末联考数学(文)试题【区级联考】天津市部分区2019届高三(上)期末数学(文科)试题【全国百强校】四川省成都市成都外国语学校2018-2019学年高二下学期期中考试文科数学试题【全国百强校】河北省武邑中学2019届高三下学期第一次模拟考试数学(文)试题湖北省武汉二中2019-2020学年高二下学期4月第二次线上测试数学试题四川省宜宾市第四中学校2019-2020学年高二下学期期中考试数学(理)试题四川省宜宾市第四中学校2019-2020学年高二下学期期中考试数学(文)试题广东省佛山市三水区三水中学2019-2020学年高二下学期第二次统考数学试题黑龙江省大庆实验中学2019届高三普通高等学校招生全国统一考试文科数学模拟试题



