专题03 解三角形
【要点提炼】
正弦定理、余弦定理、三角形面积公式
(1)正弦定理
在△ABC中,![]() =
=![]() =
=![]() =2R(R为△ABC的外接圆半径);
=2R(R为△ABC的外接圆半径);
变形:a=2Rsin A,sin A=![]() ,
,
a∶b∶c=sin A∶sin B∶sin C等.
(2)余弦定理
在△ABC中,a2=b2+c2-2bccos A;
变形:b2+c2-a2=2bccos A,cos A=![]() .
.
(3)三角形面积公式
S△ABC=![]() absin C=
absin C=![]() bcsin A=
bcsin A=![]() acsin B.
acsin B.
【方法指导】
常见三解三角形的技巧:
1、掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
2、解题时要注意:一是数形结合,通过图像所经过的特殊点与图像的对称性等来寻找突破口;二是转化意识,如判断三角形的形状可转化为对三角形的边长或内角的探求;三是方程意识,分析图形的特点,寻找关于参数的方程,解方程.
3、解三角形的实际应用问题是测量问题,如测量角度问题,仰角、俯角、方位角、视角等;测量距离问题;测量高度问题等.此类问题的关键在于通过构造三角形,应用正弦定理、余弦定理进行求解测量.4、解三角形与其他知识的综合
(1)、解三角形的应用中要注意与基本不等式的结合,以此考查三角形中有关边、角的范围问题.利用正弦定理、余弦定理与三角形的面积公式,建立如“a+b;ab;a2+b2”之间的等量关系与不等关系,通过基本不等式考查相关范围问题.
(2)、注意与三角函数的图象与性质的综合考查,将两者结合起来,既考查解三角形问题,也注重对三角函数的化简、计算及考查相关性质等.
命题点一 平面几何图形中的解三角形问题
【典例1】 (2021·江西高三其他模拟(理))如图,在中,,,点D在线段上.
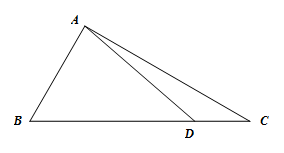
(1)若,求的长;
(2)若,且,求的值.
【答案】(1);(2).
【解析】
(1)利用正弦定理求解即可.
(2)用余弦定理求出,在两个三角形中用正弦定理得出,代入值求解即可.
【详解】
解:(1)∵,且∴,∴
(2)∵,
故算得,
在中,利用正弦定理有,
在中,有
∴,
∵,∴
∴
【方法总结】
解决以平面几何为载体的解三角形问题,主要注意以下几个方面:
1.充分利用平面几何图形的性质;
2.出现多个三角形时,从条件较多的三角形突破求解;
3.四边形问题要转化到三角形中去求解;
4.通过三角形中的不等式关系(如大边对大角,最大角一定大于或等于 )确定角的范围.
【拓展练习】
1.(2020·湖南长沙市·雅礼中学高三月考)如图,在直角中,,,,点在线段上.
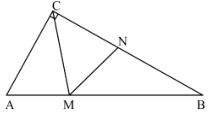
(1)若,求的长;
(2)点是线段上一点,,且,求的值.
【答案】(1)3;(2).
【解析】
(1)在中,利用正弦定理即可得到答案;
(2)由可得,在中,利用及余弦定理得,解方程组即可.
【详解】
(1)在中,已知,,,由正弦定理,
得,解得.
(2)因为,所以,解得.
在中,由余弦定理得,
,
即,
,
故.
【点睛】
本题考查正余弦定理在解三角形中的应用,考查学生的计算能力,是一道中档题.
命题点二 已知边角关系解三角形问题
【典例2】 (2019·天津高三其他模拟)在中,内角所对的边分别为 已知.
(Ⅰ)求角的大小;
(Ⅱ)设,. 求和的值.
【答案】(Ⅰ);(Ⅱ)..
【解析】
(1)利用正弦定理进行边角互化,利用三角恒等变换公式求解即可;
(2)先利用余弦定理得出,再利用正弦定理得出,得出,然后将展开求值.
【详解】
解:(Ⅰ)由已知及正弦定理可得.
因为.所以.故.
即.
整理得.
所以.
因为.所以.
(Ⅱ)根据余弦定理.,将 ,,代入解得:.因为,所以.
根据正弦定理有:,解得.
又因为,所以,则,
可求得:,.
则.
【点睛】
本题考查正弦定理、余弦定理的综合运用,考查三角函数和差角公式、二倍角公式的运用,难度一般.
【方法总结】
1、角化边:利用正弦、余弦定理把已知条件转化为只含边的关系,通过因式分解、配方等得出边的相应关系,进而求解;
2、边化角:利用正弦、余弦定理把已知条件转化为只含内角的三角函数间的关系,通过恒等变换得出内角的关系,进而求解.
【拓展练习】
2. (2019·天津南开区·高考模拟(理))在中,分别是三个内角的对边,若,且.
(1)求及的值;
(2)求的值.
【答案】(1),;(2).
【解析】
(1)由正弦定理可得,再利用二倍角的正弦公式可得,从而根据余弦定理可得;
(2)利用二倍角的正弦公式,二倍角的余弦公式求得的值,再由两角和的余弦公式可得结果.
【详解】
(1)在中,由正弦定理,
得,
,,即,
解得,
在中,由余弦定理,
得,解得或.
![]() ,.
,.
(2),
,
,
.
【点睛】
本题主要考查余弦定理、正弦定理在解三角形中的应用,属于中档题.正弦定理是解三角形的有力工具,其常见用法有以下几种:(1)知道两边和一边的对角,求另一边的对角(一定要注意讨论钝角与锐角);(2)知道两角与一个角的对边,求另一个角的对边;(3)证明化简过程中边角互化;(4)求三角形外接圆半径.
命题点三 生活中的解三角形
【典例3】(2020·全国高三专题练习)如图,一条巡逻船由南向北行驶,在A处测得山顶P在北偏东15°(∠BAC=15°)方向上,匀速向北航行20分钟到达B处,测得山顶P位于北偏东60°方向上,此时测得山顶P的仰角60°,若山高为2![]() 千米.
千米.
(1)船的航行速度是每小时多少千米?
(2)若该船继续航行10分钟到达D处,问此时山顶位于D处的南偏东什么方向?
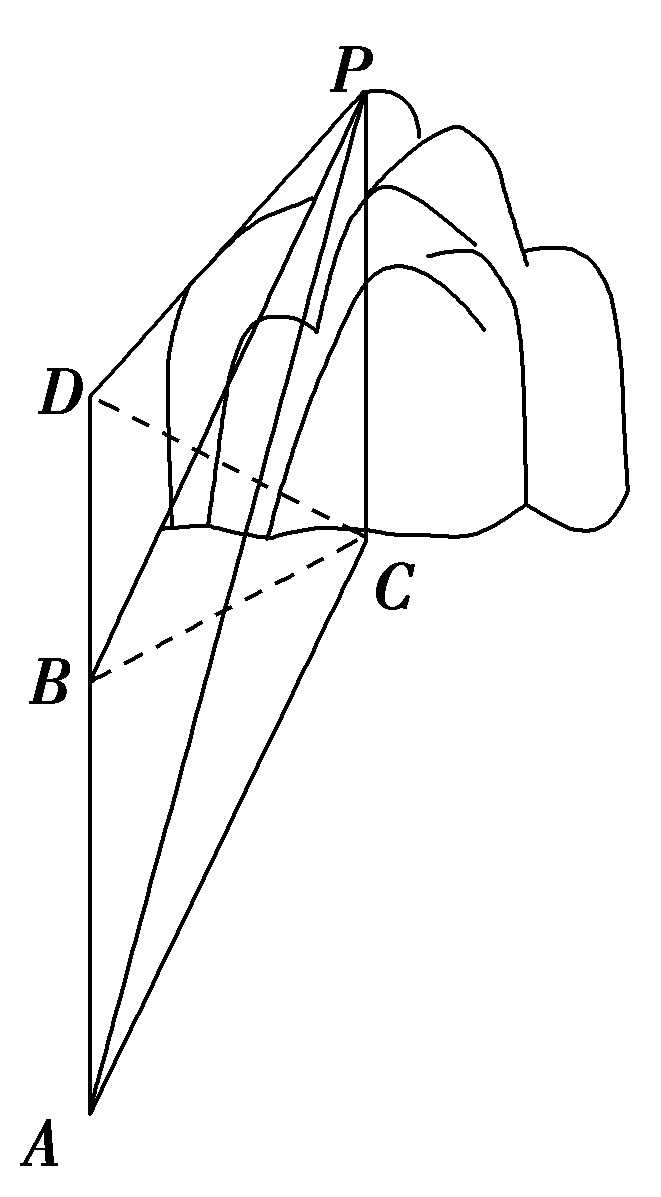
【答案】(1)船的航行速度是每小时6(![]() +1)千米.(2)山顶位于D处南偏东.
+1)千米.(2)山顶位于D处南偏东.
【解析】
(1)先在△BCP中,得到tan∠PBC,再由△ABC中,由正弦定理得AB从而得解;
(2)先在△BCD中,由余弦定理得CD,再在△BCD中,由正弦定理得sin∠CDB,从而得解.
【详解】
(1)在△BCP中,tan∠PBC=![]() ⇒BC=2.
⇒BC=2.
在△ABC中,由正弦定理得:![]() =
=![]() ⇒
⇒![]() =
=![]() ,
,
所以AB=2(![]() +1),船的航行速度是每小时6(
+1),船的航行速度是每小时6(![]() +1)千米.
+1)千米.
(2)在△BCD中,由余弦定理得:CD=![]() ,
,
在△BCD中,由正弦定理得:![]() =
=![]() ⇒sin∠CDB=
⇒sin∠CDB=![]() ,∠CDB
,∠CDB
所以,∠CDB=
所以,山顶位于D处南偏东.
【方法总结】
解三角形应用题的一般步骤:
(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.
(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.
(3)根据题意选择正弦定理或余弦定理求解.
(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.
【拓展练习】
3. (2020·全国高三专题练习)如图,某景区内有一半圆形花圃,其直径AB为6,O是圆心,且OC⊥AB.在OC上有一座观赏亭Q,其中∠AQC=,.计划在上再建一座观赏亭P,记∠POB=θ.
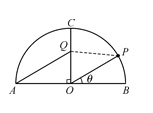
(1)当θ=时,求∠OPQ的大小;
(2)当∠OPQ越大时,游客在观赏亭P处的观赏效果越佳,求游客在观赏亭P处的观赏效果最佳时,角θ的正弦值.
【答案】(1).(2).
【解析】
(1)设∠OPQ=α,在△POQ中,用正弦定理可得含α,θ的关系式,将其展开化简并整理后得tanα=,将θ=代入得答案;
(2)令f(θ)=并利用导数求得f(θ)的最大值,即此时的,由(1)可知tanα=,得答案.
【详解】
(1)设∠OPQ=α,在△POQ中,用正弦定理可得含α,θ的关系式.
因为∠AQC=,所以∠AQO=.又OA=OB=3,所以OQ=
在△OPQ中,OQ=,OP=3,∠POQ=-θ,设∠OPQ=α,则∠PQO=-α+θ.
由正弦定理,得=,即sinα=cos(α-θ).
展开并整理,得tanα=,其中θ∈.
此时当θ=时,tanα=.因为α∈(0,π),所以α=.
故当θ=时,∠OPQ=.
(2)设f(θ)=,θ∈.
则f′(θ)==.
令f′(θ)=0,得sinθ=,记锐角θ0满足,
则,即
列表如下:
θ | (0,θ0) | θ0 | |
f′(θ) | + | 0 | - |
f(θ) | 单调递增 | 单调递减 |
由上表可知,f(θ0)=是极大值,也是最大值.
由(1)可知tanα=f(θ)>0,则, tanα单调递增
则当tanα取最大值时,α也取得最大值.
故游客在观赏亭P处的观赏效果最佳时,sinθ=.
【点睛】
本题考查三角函数和解三角形的实际应用,应优先建模,将实际问题转化为熟悉的数学问题,进而由正弦定理构建对应关系,还考查了利用导数求函数的最值,属于难题.
【专题训练】
一、单选题
(2020·四川内江市·高三一模(理))
 ,
,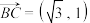 ,则
,则 的面积为( )
的面积为( )A. | B. | C. | D. |
【知识点】 三角形面积公式及其应用解读 坐标计算向量的模解读 向量夹角的坐标表示
(2020·四川省阆中东风中学校高三月考(文))
(2018·北京朝阳区·高三其他模拟(理))
(2021·四川成都市·高三月考(文))
(2021·山西吕梁市·高三一模(理))
 边形等分成
边形等分成 个等腰三角形(如图所示),当
个等腰三角形(如图所示),当 变得很大时,这
变得很大时,这 个等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,估计
个等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,估计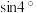 的值为( )
的值为( )
A. | B.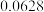 | C.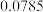 | D. |
【知识点】 三角形面积公式及其应用解读
(2020·全国高三专题练习)
 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,其中
,其中 为钝角,且满足
为钝角,且满足 ,
, ,若点
,若点 与点
与点 在
在 的两侧,且
的两侧,且 ,
, ,
, ,
, 四点共圆,则四边形
四点共圆,则四边形 面积的最大值为( )
面积的最大值为( )A.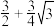 | B.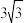 | C. | D. |
(2020·沙坪坝区·重庆一中高三月考(理))
 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, 且
且 ,
, ,若
,若 ,
, 变化时,
变化时,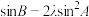 存在最大值,则正数
存在最大值,则正数 的取值范围是( )
的取值范围是( )A.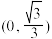 | B.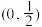 | C.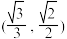 | D.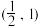 |
【知识点】 辅助角公式解读 正弦定理边角互化的应用解读
二、多选题
(2020·全国高三专题练习)
 中,D在线段
中,D在线段 上,且
上,且 若
若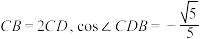 ,则( )
,则( )A.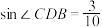 | B. 的面积为8 的面积为8 |
C. 的周长为 的周长为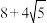 | D. 为钝角三角形 为钝角三角形 |
(2020·海南枫叶国际学校高一期中)
(2017·山东德州市·高考模拟(文))
A.在 ABC中,a:b:c=sin A:sin B:sin C ABC中,a:b:c=sin A:sin B:sin C |
B.在 ABC中,若sin 2A=sin 2B,则a=b ABC中,若sin 2A=sin 2B,则a=b |
C.在 ABC中,若sin A>sin B,则A>B,若A>B,则sin A>sin B都成立 ABC中,若sin A>sin B,则A>B,若A>B,则sin A>sin B都成立 |
D.在 ABC中, ABC中, |
三、填空题
(2020·河南开封市·高三一模(理))
(2020·全国高三专题练习(理))
(2020·合肥市第六中学高三其他模拟(理))
 ,再由点C沿北偏东
,再由点C沿北偏东 方向走10米到位置D,测得
方向走10米到位置D,测得 ,则铁塔AB的高为
,则铁塔AB的高为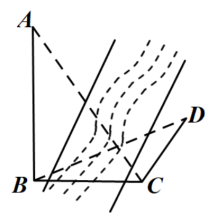
(2020·重庆北碚区·西南大学附中高三月考)
 中,角A、B、C的对边长分别为a、b、c,且
中,角A、B、C的对边长分别为a、b、c,且 ,
, ,则
,则 面积的最大值为
面积的最大值为四、解答题
(2021·安徽淮南市·高三一模(理))
 的内角A,B,C的对边为a,b,c,且
的内角A,B,C的对边为a,b,c,且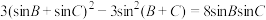 .
.(1)求
 的值;
的值;(2)若
 的面积为
的面积为 ,求
,求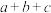 的最小值.
的最小值.
(2020·上海高三专题练习)
 是某个历史文物展览厅的俯视图,点
是某个历史文物展览厅的俯视图,点 在
在 上,在梯形
上,在梯形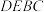 区域内部展示文物,
区域内部展示文物, 是玻璃幕墙,游客只能在△
是玻璃幕墙,游客只能在△ 区域内参观.在
区域内参观.在 上点
上点 处安装一可旋转的监控摄像头,
处安装一可旋转的监控摄像头,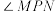 为监控角,其中
为监控角,其中 、
、 在线段
在线段 (含端点)上,且点
(含端点)上,且点 在点
在点 的右下方.经测量得知:
的右下方.经测量得知: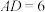 米,
米,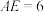 米,
米,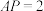 米,
米, .记
.记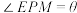 (弧度),监控摄像头的可视区域△
(弧度),监控摄像头的可视区域△ 的面积为
的面积为 平方米.
平方米.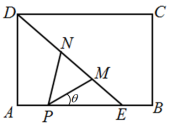


(1)分别求线段
 、
、 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;(2)求
 的最小值.
的最小值.
【知识点】 求三角形面积的最值或范围
(2020·安徽省六安中学高三开学考试(理))
 中,角
中,角 的对边分别为
的对边分别为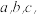
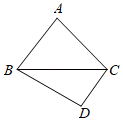
 .
.
(1)求
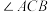 的大小;
的大小;(2)若
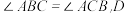 为△
为△ 外一点,
外一点, ,求四边形
,求四边形 面积的最大值.
面积的最大值.


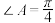 ,
, ,
, ,则
,则 (
(

 ,
, ,
,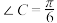 ,则
,则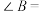 (
(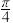


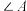 ,
, ,
,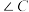 的对边,如果
的对边,如果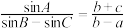 ,那么
,那么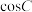 的值为(
的值为(

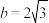 ,
,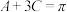 ,则下列结论正确的是(
,则下列结论正确的是(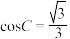
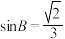


 ,
,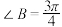 ,
, ,
,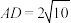 ,若
,若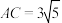 ,则
,则
 为
为 平分线,若
平分线,若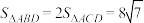 ,且
,且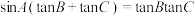 ,则
,则

