专题05 数列求和及综合应用
【要点提炼】
1.常用公式:12+22+32+42+…+n2=.
2.(1)数列通项an与前n项和Sn的关系为an=
(2)应用an与Sn的关系式f(an,Sn)=0时,应特别注意n=1时的情况,防止产生错误.
3.数列求和
(1)分组转化法:一个数列既不是等差数列,也不是等比数列,若将这个数列适当拆开,重新组合,就会变成几个可以求和的部分,分别求和,然后再合并.
(2)错位相减法:主要用于求数列{an·bn}的前n项和,其中{an},{bn}分别是等差数列和等比数列.
(3)裂项相消法:即将数列的通项分成两个式子的代数差的形式,然后通过累加抵消中间若干项的方法,裂项相消法适用于形如(其中{an}是各项均不为零的等差数列,c为常数)的数列.
温馨提醒 裂项求和时,易把系数写成它的倒数或忘记系数导致错误.
4.数列与函数、不等式的交汇
数列与函数的综合问题一般是利用函数作为背景,给出数列所满足的条件,通常利用点在曲线上给出Sn的表达式,还有以曲线上的切点为背景的问题,解决这类问题的关键在于利用数列与函数的对应关系,将条件进行准确的转化.数列与不等式的综合问题一般以数列为载体,考查不等关系或恒成立问题.
【方法指导】
1、某些数列的求和是将数列转化为若干个可求和的新数列的和或差,从而求得原数列的和.注意在含有字母的数列中对字母的讨论.
(1)若数列的通项公式为 ,且,为等差数列或等比数列,则可以采用分组求和法求数列的前项和;
(2)若数列 的通项公式为 ,且数列,是等比数列或等差数列,则可以采用分组求和法求数列的前 项和;
(3)若数列的通项公式中有 等特征,根据正负号分组求和.
2、一般地,若数列 是等差数列,是等比数列,求数列的前 项和,则可以采用错位相减法求和.一般是先将和式两边乘以等比数列的公比,然后做差求解;
3、在写出 与的表达式时,应特别注意将两式“错位对齐”,以便下一步准确写出的表达式;
4、在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.
5、(1)利用裂项相消法求和时,应注意抵消后并不一定只剩下第一项和最后一项,也有可能前面剩两三项,后面也剩两三项;
(2)将通项公式裂项后,有时候需要调整前面的系数,使裂开的两项之差和系数之积与原通项公式相等.
6、数列与不等式相结合问题的处理方法:
(1)如果是证明题,那么要灵活选择不等式的证明方法,如比较法、综合法、分析法、放缩法等.
(2)如果是解不等式问题,那么要使用不等式的各种不同解法,如列表法、因式分解法等.总之解决这类问题把数列和不等式的知识巧妙结合起来综合处理就行了
命题点一 利用分组求和法求和
【典例1】 (2021·广西高三其他模拟(文))已知数列的前项和是,且满足.
(1)求数列的通项公式;
(2)若,求数列由组成,求的前项和.
【答案】(1);(2).
【分析】
(1)根据与的关系,结合递推式可得数列为等比数列,进而可得通项公式;
(2)分为为奇数和偶数两种情形,结合等差数列和等比数列前项和公式可得结果.
【详解】
(1)依题意:当时,有:又,故
干①,当时,有②,
①②得:化简得,
是以1为首项,2为公比的等比数列,
(2)当为偶数时
当为奇数时
【方法总结】
某些数列的求和是将数列转化为若干个可求和的新数列的和或差,从而求得原数列的和.注意在含有字母的数列中对字母的讨论.
(1)若数列的通项公式为 ,且,为等差数列或等比数列,则可以采用分组求和法求数列的前项和;
(2)若数列 的通项公式为 ,且数列,是等比数列或等差数列,则可以采用分组求和法求数列的前 项和;
(3)若数列的通项公式中有 等特征,根据正负号分组求和.
【拓展练习】
1、(2020·福建莆田市·高三其他模拟)已知等比数列的公比为q.
(1)试问数列一定是等比数列吗?说明你的理由;
(2)在①,②,③这三个条件中任选两个,补充在下面的问题中并解答.
问题:若 ,求的通项公式及数列的前n项和.
注:如果选择多种情况解答,则按第一种情况计分.
【答案】(1)不一定,时,不是等比数列;(2)答案见解析.
【分析】
(1)时,,从而确定数列是否为等比数列;
(2)选①②,由得,求得后可得通项公式,然后用分组求和法求得,对分偶数和奇数分别求和化简.
选②③,由得,由得,然后求得后得通项公式,然后用分组求和法求得,对分偶数和奇数分别求和化简.
选①③,由得,从而得,从而可得,然后用分组求和法求得,对分偶数和奇数分别求和化简.
【详解】
(1)数列不一定是等比数列,理由如下:
时,,不是等比数列,
时,是等比数列,
故数列不一定是等比数列;
(2)选①②,
由,得,,∵,∴,
∴,
,
为偶数时,,
为奇数时,,
选②③,
由,得,,又,,
∴,,∴,
,
当为偶数时,,
当为奇数时,;
选①③,
由,得,又,∴,∴,
,
为偶数时,,
为奇数时,,
【点睛】
关键点点睛:本题考查等比数列的判断,考查求等比数列的通项公式和分组求和法求和.涉及到,因此求和时按的奇数和偶数分类讨论,偶数时正好相邻两项合并求和.数列求和的几种方法一定要掌握:公式法、错位相减法、裂项相消法、分组(并项)求和法,倒序相加法.
命题点二 利用错位相减法求和
【典例2】(2021·黑龙江齐齐哈尔市实验中学高三期末(理))设数列的前n项和为,已知,.
(1)求证:数列为等比数列
(2)若数列满足:,,求数列的通项公式及数列的前n项和.
【答案】(1)证明见解析;(2),.
【分析】
(1)由,得,两式相减得,结合,计算出,确定,从而证明出等比数列;
(2)由(1)求得,对的递推关系式变形得数列是首项为1,公差为1的等差数列.,从而求得,得出后用错位相减法求得和.
【详解】
(1)证明:由,,得,
两式相减,得,
因为,由,得,所以,
所以对任意部成立.
所以数列为等比数列,首项为1,公比为2;
(2)由(1)知,,,
即,
因为,所以数列是首项为1,公差为1的等差数列.
所以,所以.
②设数列的前n项和,,
相减可得,
化简可得数列的前n项和为.
【点睛】
本题考查求等差、等比数列的通项公式,错位相减法求和.数列求和的常用方法:
设数列是等差数列,是等比数列,
(1)公式法:等差数列或等比数列的求和直接应用公式求和;
(2)错位相减法:数列的前项和应用错位相减法;
(3)裂项相消法;数列(为常数,)的前项和用裂项相消法;
(4)分组(并项)求和法:数列用分组求和法,如果数列中的项出现正负相间等特征时可能用并项求和法;
(5)倒序相加法:满足(为常数)的数列,需用倒序相加法求和.
【方法总结】
1、一般地,若数列 是等差数列,是等比数列,求数列的前 项和,则可以采用错位相减法求和.一般是先将和式两边乘以等比数列的公比,然后做差求解;
2、在写出 与的表达式时,应特别注意将两式“错位对齐”,以便下一步准确写出的表达式;
3、在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.
【拓展练习】
2、(2020·四川宜宾市·高三一模(理))已知递增数列满足,,且是方程的两根,数列的前项和为,且.
(1)求数列,的通项公式;
(2)记,求数列的前项和.
【答案】(1),;(2).
【分析】
(1)求出,即得数列的通项公式;利用求的通项公式;
(2)先求出,再利用错位相减法求和.
【详解】
(1)因为方程两根为或7,
又、是方程的两根,数列是递增的等差数列,
,,设公差为,则,解得,.
.
对于数列,,
当时,,解得;
当时,,
整理得,即,所以数列是等比数列,
(2),
数列的前项和,,
......
两式相减可得......,
.
【点睛】
方法点睛:数列求和常用的方法有:(1)公式法;(2)错位相减法;(3)裂项相消法;(4)分组求和法;(5)倒序相加法.要根据数列通项的特征灵活选择求和方法.
命题点三 利用裂项相消法求和
【典例3】(2021·福建漳州市·高三其他模拟)已知各项均为正数的等比数列的前项和为,且,.
(1)若等差数列满足,求,的通项公式;
(2)若___________,求数列的前项和.
在①;②;③这三个条件中任选一个补充到第(2)问中,并对其求解.
注:如果选择多个条件分别求解,按第一个解答计分.
【答案】(1),;(2)答案见解析.
【分析】
(1)利用等比数列的通项公式与求和公式求出和,得到数列的通项公式,再求出对应等差数列的前两项和公差,即可得数列的通项公式;(2)根据已知条件进行整理,得出数列的通项公式,进而利用裂项相消法即可求解.
【详解】
(1)设数列的公比为,则.
,
,解得:或,
又因为各项均为正数,
所以,
又,
,
代入得,,
,
则,,
设数列的公差为,
∴,
则.
(2)选择①:
,,
则,
.
选择②:
,,
则,
,
.
选择③:
由(1)知,
.
,
.
【点睛】
本题考查的核心是裂项求和,使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源与目的.
【方法总结】
(1)利用裂项相消法求和时,应注意抵消后并不一定只剩下第一项和最后一项,也有可能前面剩两三项,后面也剩两三项;
(2)将通项公式裂项后,有时候需要调整前面的系数,使裂开的两项之差和系数之积与原通项公式相等.
【拓展练习】
3、(2020·梅河口市第五中学高三月考(理))已知数列为正项等比数列,满足,且构成等差数列,数列满足.
(1)求数列,的通项公式;
(2)若数列的前![]() 项和为,数列满足,求数列的前
项和为,数列满足,求数列的前![]() 项和.
项和.
【答案】(1);(2)
【分析】
(1)由题意,根据等比数列性质,以及等差中项可求得公比,即可求得,代入可求得;
(2)由(1)可求得的前n项和,带入求得,再利用裂项相消求得.
【详解】
解:(1)设等比数列的公比为,由题意,得
解得或(舍)
又所以
(2).
【点睛】
本题考查了数列的知识,掌握等差等比数列的性质、通项是解题的关键,同时也需要掌握好数列求和的裂项相消,属于较为基础题.
命题点四 数列不等式问题
【典例4】(2020·全国高三其他模拟(理))已知数列的首项为0,.
(1)证明数列是等差数列,并求出数列的通项公式;
(2)已知数列的前项和为,且数列满足,若不等式对一切恒成立,求的取值范围.
【答案】(1)证明见解析,;(2).
【分析】
(1)将递推公式构造成,再根据等差数列的定义构造得到结论,并求通项公式;(2)由(1)可知,利用错位相减法求和,再分为奇数和偶数两种情况讨论求的取值范围.
【详解】
(1)证明:∵,∴,
∴,
∴,
∴数列是首项为1,公差为2的等差数列.
∴,∴.
(2)由题可知,,
,
两式相减得,
∴.
∴,
若为偶数,则,∴;
若为奇数,则,∴,∴.
综上,.
【点睛】
方法点睛:本题第二问涉及数列求和的方法,一般数列求和包含
1.公式法,利用等差和等比数列的前项和公式求解;
2.错位相减法求和,适用于等差数列乘以等比数列的数列求和;
3.裂项相消法求和,适用于能变形为;
4.分组转化法求和,适用于;
5.倒序相加法求和.
【方法总结】
数列与不等式相结合问题的处理方法:
(1)如果是证明题,那么要灵活选择不等式的证明方法,如比较法、综合法、分析法、放缩法等.
(2)如果是解不等式问题,那么要使用不等式的各种不同解法,如列表法、因式分解法等.总之解决这类问题把数列和不等式的知识巧妙结合起来综合处理就行了.
【拓展练习】
4、(2020·江苏苏州市·常熟中学高三其他模拟)在数列中,,,,其中.
(1)证明:数列为等差数列,并求出通项公式;
(2)设,数列的前项和为,求;
(3)已知当且时,,其中,求满足等式的所有的值之和.
【答案】(1)证明详见解析;;(2)=8-;(3)5.
【分析】
(1)根据等差数列的定义进行证明,结合首项和公差可得通项公式;
(2)根据可得,然后利用错位相减法进行求和;
(3)先把条件转化为,结合及等比数列求和得出时无解,验证前5项可得结果.
【详解】
(1)证明:
∴数列为等差数列,又,∴
(2)因为,
所以=. ①
=. ②
①-②,得=-.
故=-=8--=8-.
(3)由(1)得等式
可化为
即
∴
∵当时,,
∴,,…,,
∴
∴当时,;
当时,经验算时等号成立,
∴满足等式的所有,其和为5.
【点睛】
本题主要考查等差数列的判定,错位相减法求等,等差数列的判定一般利用定义法进行证明,错位相减法求和时注意项数及尾项符号,侧重考查数学运算的核心素养.
【专题训练】
一、单选题
(2021·全国高三其他模拟)
(2021·安徽淮南市·高三一模(文))
(2021·河南郑州市·高三一模(文))
 为数列
为数列 的前
的前 项和,
项和,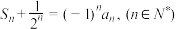 ,则数列
,则数列 的前
的前 项和为( )
项和为( )A.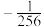 | B.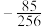 | C. | D.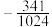 |
【知识点】 分组(并项)法求和 利用an与sn关系求通项或项
(2020·全国高三专题练习)
 满足
满足 ,且
,且 ,其前n项之和为
,其前n项之和为 ,则满足不等式
,则满足不等式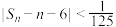 的最小整数n是
的最小整数n是| A.5 | B.6 | C.7 | D.8 |
【知识点】 由递推关系式求通项公式 分组(并项)法求和
(2020·湖南长沙市·雅礼中学高三其他模拟(理))
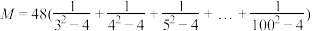 ,则与
,则与 最接近的整数为( )
最接近的整数为( )| A.18 | B.20 | C.24 | D.25 |
【知识点】 裂项相消法求和
(2020·合肥市第六中学高三其他模拟(理))
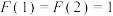 ,
,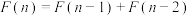 ,
,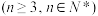 .此数列在现代物理及化学等领域有着广泛的应用,若此数列被4整除后的余数构成一个新的数列
.此数列在现代物理及化学等领域有着广泛的应用,若此数列被4整除后的余数构成一个新的数列 ,又记数列
,又记数列 满足
满足 ,
, ,
,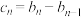
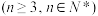 ,则
,则 的值为( )
的值为( )| A.4 | B.2 | C.1 | D.0 |
(2021·全国高三其他模拟(理))
二、多选题
(2021·山东高三专题练习)
 的首项为4,且满足
的首项为4,且满足 ,则( )
,则( )A. 为等差数列 为等差数列 |
B. 为递增数列 为递增数列 |
C. 的前 的前 项和 项和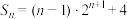 |
D.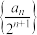 的前 的前 项和 项和 |
【知识点】 判断数列的增减性 由递推关系证明数列是等差数列 错位相减法求和
(2020·江苏苏州市·高二期中)
 的前
的前 项和为
项和为 ,已知
,已知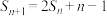 ,则下列结论正确的是( )
,则下列结论正确的是( )A.数列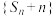 为等比数列 为等比数列 |
B.数列 的通项公式为 的通项公式为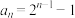 |
C.数列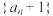 为等比数列 为等比数列 |
D.数列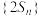 的前 的前 项和为 项和为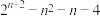 |
(2020·湖南常德市一中高三月考)
 是无穷数列,若存在正整数k,使得对任意
是无穷数列,若存在正整数k,使得对任意 ,均有
,均有 ,则称
,则称 是间隔递增数列,k是
是间隔递增数列,k是 的间隔数,下列说法正确的是( )
的间隔数,下列说法正确的是( )| A.公比大于1的等比数列一定是间隔递增数列 |
B.已知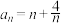 ,则 ,则 是间隔递增数列 是间隔递增数列 |
C.已知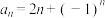 ,则 ,则 是间隔递增数列且最小间隔数是2 是间隔递增数列且最小间隔数是2 |
D.已知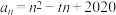 ,若 ,若 是间隔递增数列且最小间隔数是3,则 是间隔递增数列且最小间隔数是3,则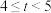 |
【知识点】 数列新定义 数列不等式恒成立问题
三、填空题
(2021·福建高三其他模拟)
 的前
的前 项和为
项和为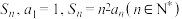 ,则数列
,则数列 的通项公式为
的通项公式为【知识点】 累乘法求数列通项 利用an与sn关系求通项或项
(2020·河南高三其他模拟(理))
 ,若
,若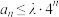 对于任意nN*恒成立,则实数
对于任意nN*恒成立,则实数 的取值范围是
的取值范围是【知识点】 根据数列的单调性求参数
(2021·宁夏吴忠市·高三一模(理))
 ,
, ,其中数列
,其中数列 满足
满足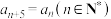 ,前n项和为
,前n项和为 满足
满足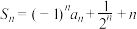
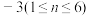 ;数列
;数列 满足:
满足: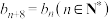 ,且
,且 ,
, ,则数列
,则数列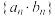 的第2024项的值为
的第2024项的值为【知识点】 利用an与sn关系求通项或项 数列周期性的应用
四、解答题
(2020·江西吉安市·高三其他模拟(理))
 满足
满足 ,
,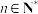 .
.(1)求数列
 的通项公式;
的通项公式;(2)设等差数列
 的前
的前 项和为
项和为 ,且
,且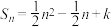 ,令
,令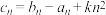 ,求数列
,求数列 的前
的前 项和
项和 .
.
【知识点】 求等差数列前n项和 分组(并项)法求和 利用an与sn关系求通项或项
(2021·江西上饶市·高三一模(理))
 大于1的等比数列
大于1的等比数列 满足
满足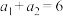 ,
, .
.(1)求
 的通项公式;
的通项公式;(2)令
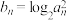 ,求数列
,求数列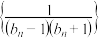 的前
的前 项和
项和 .
.
【知识点】 等比数列通项公式的基本量计算 裂项相消法求和
(2021·江西上饶市·高三其他模拟(理))
 ,
, ,
,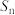 是其前
是其前 项和,且满足
项和,且满足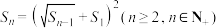 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
 ,求
,求 的前
的前 项和
项和 .
.
【知识点】 利用定义求等差数列通项公式 由Sn求通项公式 裂项相消法求和
(2021·湖北高三一模)
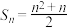 ;②
;② ,
,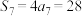 ;③
;③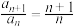 ,
, 这三个条件中任选一个补充在下面的问题中,并加解答.
这三个条件中任选一个补充在下面的问题中,并加解答.问题:设数列
 的前
的前 项和为
项和为 ,___________,若
,___________,若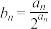 ,求数列
,求数列 的前
的前 项和.
项和.注:如果选择多个条件分别解答,按第一解答计分.
(2021·江苏高三一模)
 满足
满足 .
.(1)求数列
 的通项公式;
的通项公式;(2)记数列
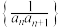 的前n项和为
的前n项和为 .若
.若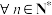 ,
,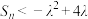 (
( 为偶数),求
为偶数),求 的值.
的值.
【知识点】 利用定义求等差数列通项公式 裂项相消法求和 数列不等式恒成立问题


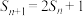 ,则
,则 (
( ,
, ,则
,则
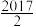

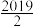

 ,若数列
,若数列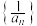 的前
的前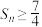 ,则
,则

