名校
解题方法
1 . 若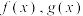 是定义在
是定义在 上的增函数,其中
上的增函数,其中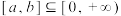 ,存在函数
,存在函数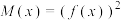 ,
,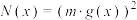 ,且函数
,且函数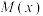 图像上存在两点
图像上存在两点 ,
,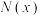 图像上存在两点
图像上存在两点 ,其中
,其中 两点横坐标相等,
两点横坐标相等,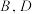 两点横坐标相等,且
两点横坐标相等,且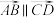 ,则称
,则称 在
在 上可以对
上可以对 进行“
进行“ 型平行追逐”,即
型平行追逐”,即 是
是 在
在 上的“
上的“ 型平行追逐函数”. 已知
型平行追逐函数”. 已知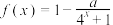 是定义在
是定义在 上的奇函数,
上的奇函数,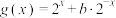 是定义在
是定义在 上的偶函数.
上的偶函数.
(1)求满足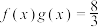 的
的 的值;
的值;
(2)设函数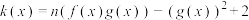 ,若不等式
,若不等式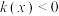 对任意的
对任意的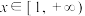 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若函数 是
是 在
在 上的“
上的“ 型平行追逐函数”,求正数
型平行追逐函数”,求正数 的取值范围.
的取值范围.
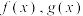 是定义在
是定义在 上的增函数,其中
上的增函数,其中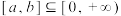 ,存在函数
,存在函数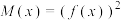 ,
,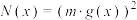 ,且函数
,且函数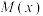 图像上存在两点
图像上存在两点 ,
,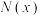 图像上存在两点
图像上存在两点 ,其中
,其中 两点横坐标相等,
两点横坐标相等,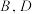 两点横坐标相等,且
两点横坐标相等,且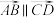 ,则称
,则称 在
在 上可以对
上可以对 进行“
进行“ 型平行追逐”,即
型平行追逐”,即 是
是 在
在 上的“
上的“ 型平行追逐函数”. 已知
型平行追逐函数”. 已知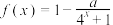 是定义在
是定义在 上的奇函数,
上的奇函数,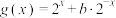 是定义在
是定义在 上的偶函数.
上的偶函数.(1)求满足
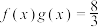 的
的 的值;
的值;(2)设函数
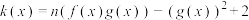 ,若不等式
,若不等式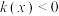 对任意的
对任意的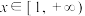 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若函数
 是
是 在
在 上的“
上的“ 型平行追逐函数”,求正数
型平行追逐函数”,求正数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
2 . 已知函数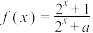 为奇函数.
为奇函数.
(1)求实数a的值;
(2)判断函数 的单调性(不用证明);
的单调性(不用证明);
(3)设函数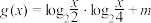 ,若对任意的
,若对任意的 ,总存在
,总存在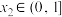 ,使得
,使得 成立,求实数m的取值范围.
成立,求实数m的取值范围.
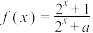 为奇函数.
为奇函数.(1)求实数a的值;
(2)判断函数
 的单调性(不用证明);
的单调性(不用证明);(3)设函数
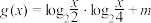 ,若对任意的
,若对任意的 ,总存在
,总存在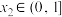 ,使得
,使得 成立,求实数m的取值范围.
成立,求实数m的取值范围.
您最近一年使用:0次
2024-06-07更新
|
968次组卷
|
2卷引用:广东省汕头市潮阳实验学校2023-2024学年高一下学期期中考试数学试题
名校
3 . 已知函数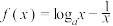 (
( ).
).
(1)若 在
在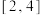 上的最小值为
上的最小值为 ,求a的值;
,求a的值;
(2)证明: 存在唯一零点
存在唯一零点 且满足
且满足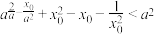 .
.
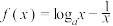 (
( ).
).(1)若
 在
在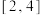 上的最小值为
上的最小值为 ,求a的值;
,求a的值;(2)证明:
 存在唯一零点
存在唯一零点 且满足
且满足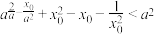 .
.
您最近一年使用:0次
名校
4 . 已知函数 和
和 的定义域分别为
的定义域分别为 和
和 ,若对任意
,若对任意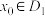 ,恰好存在
,恰好存在 个不同的实数
个不同的实数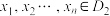 ,使得
,使得 (其中
(其中 ),则称
),则称 为
为 的“
的“ 重覆盖函数”.
重覆盖函数”.
(1)试判断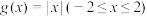 是否为
是否为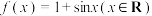 的“2重覆盖函数”?请说明理由;
的“2重覆盖函数”?请说明理由;
(2)若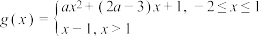 ,为
,为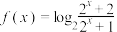 ,的“2重覆盖函数”,求实数
,的“2重覆盖函数”,求实数 的取值范围;
的取值范围;
(3)函数 表示不超过
表示不超过 的最大整数,如
的最大整数,如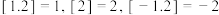 .若
.若 为
为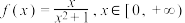 的“2024重覆盖函数”请直接写出正实数
的“2024重覆盖函数”请直接写出正实数 的取值范围.
的取值范围.
 和
和 的定义域分别为
的定义域分别为 和
和 ,若对任意
,若对任意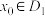 ,恰好存在
,恰好存在 个不同的实数
个不同的实数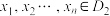 ,使得
,使得 (其中
(其中 ),则称
),则称 为
为 的“
的“ 重覆盖函数”.
重覆盖函数”.(1)试判断
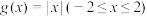 是否为
是否为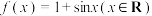 的“2重覆盖函数”?请说明理由;
的“2重覆盖函数”?请说明理由;(2)若
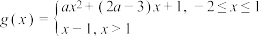 ,为
,为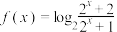 ,的“2重覆盖函数”,求实数
,的“2重覆盖函数”,求实数 的取值范围;
的取值范围;(3)函数
 表示不超过
表示不超过 的最大整数,如
的最大整数,如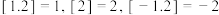 .若
.若 为
为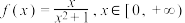 的“2024重覆盖函数”请直接写出正实数
的“2024重覆盖函数”请直接写出正实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-03-29更新
|
248次组卷
|
2卷引用:广东省广州市第六中学2023-2024学年高一下学期期中考试数学试题
名校
解题方法
5 . 已知函数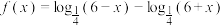 .
.
(1)判断函数 的奇偶性;
的奇偶性;
(2)判断函数 的单调性;
的单调性;
(3)若 ,求实数
,求实数 的取值范围.
的取值范围.
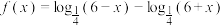 .
.(1)判断函数
 的奇偶性;
的奇偶性;(2)判断函数
 的单调性;
的单调性;(3)若
 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-02-04更新
|
222次组卷
|
3卷引用:广东省湛江第一中学2023-2024学年高一上学期第二次大考数学试题
解题方法
6 . 已知二次函数 满足
满足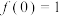 ,且
,且 ,
, 为偶函数,且当
为偶函数,且当 时,
时, .
. 的解析式;
的解析式;
(2)在给定的坐标系内画出 的图象;
的图象;
(3)讨论函数 (
(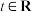 )的零点个数.
)的零点个数.
 满足
满足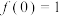 ,且
,且 ,
, 为偶函数,且当
为偶函数,且当 时,
时, .
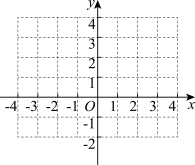
.
 的解析式;
的解析式;(2)在给定的坐标系内画出
 的图象;
的图象;(3)讨论函数
 (
(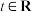 )的零点个数.
)的零点个数.
您最近一年使用:0次
2024-01-26更新
|
134次组卷
|
2卷引用:广东省茂名市2023-2024学年高一上学期期末质量监测数学试题
名校
解题方法
7 . 某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值 与这种新材料的含量
与这种新材料的含量 (单位:克)的关系:当
(单位:克)的关系:当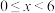 时,
时, 是
是 的二次函数;当
的二次函数;当 时,
时, 测得数据如下表所示(部分):
测得数据如下表所示(部分):
(1)求 关于
关于 的函数关系式
的函数关系式
(2)求函数 的最大值.
的最大值.
 与这种新材料的含量
与这种新材料的含量 (单位:克)的关系:当
(单位:克)的关系:当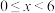 时,
时, 是
是 的二次函数;当
的二次函数;当 时,
时, 测得数据如下表所示(部分):
测得数据如下表所示(部分): (单位:克) (单位:克) | 0 | 1 | 2 | 9 |
 | 0 | 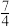 | 3 |  |
 关于
关于 的函数关系式
的函数关系式
(2)求函数
 的最大值.
的最大值.
您最近一年使用:0次
2024-06-13更新
|
44次组卷
|
2卷引用:广东省湛江第一中学2023-2024学年高一上学期第二次大考数学试题
名校
8 . 已知函数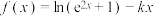 为偶函数.
为偶函数.
(1)求实数 的值;
的值;
(2)求函数 的值域;
的值域;
(3)若函数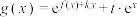 ,
, ,那么是否存在实数
,那么是否存在实数 ,使得
,使得 的最小值为1?若存在,求出
的最小值为1?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
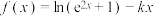 为偶函数.
为偶函数.(1)求实数
 的值;
的值;(2)求函数
 的值域;
的值域;(3)若函数
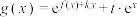 ,
, ,那么是否存在实数
,那么是否存在实数 ,使得
,使得 的最小值为1?若存在,求出
的最小值为1?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
您最近一年使用:0次
名校
解题方法
9 . 已知函数 是定义域上的奇函数,且
是定义域上的奇函数,且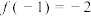 .
.
(1)判断并证明函数 在
在 上的单调性;
上的单调性;
(2)令函数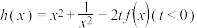 ,若对
,若对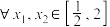 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
 是定义域上的奇函数,且
是定义域上的奇函数,且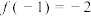 .
.(1)判断并证明函数
 在
在 上的单调性;
上的单调性;(2)令函数
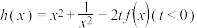 ,若对
,若对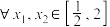 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
10 . 已知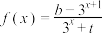 是定义在
是定义在 上的奇函数.
上的奇函数.
(1)求 的解析式;
的解析式;
(2)若对于 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
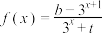 是定义在
是定义在 上的奇函数.
上的奇函数.(1)求
 的解析式;
的解析式;(2)若对于
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次



