名校
解题方法
1 . 在 中,设A,B,C所对的边分别为a,b,c,已知
中,设A,B,C所对的边分别为a,b,c,已知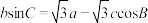 .
.
(1)求 的大小;
的大小;
(2)若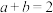 ,求边长
,求边长 的取值范围;
的取值范围;
(3)若 ,求
,求 面积
面积 的最大值.
的最大值.
 中,设A,B,C所对的边分别为a,b,c,已知
中,设A,B,C所对的边分别为a,b,c,已知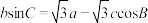 .
.(1)求
 的大小;
的大小;(2)若
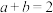 ,求边长
,求边长 的取值范围;
的取值范围;(3)若
 ,求
,求 面积
面积 的最大值.
的最大值.
您最近一年使用:0次
2 . 已知椭圆 :
: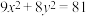 ,直线
,直线 :
: 交椭圆于M,N两点,T为椭圆的右顶点,
交椭圆于M,N两点,T为椭圆的右顶点,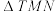 的内切圆为圆Q.
的内切圆为圆Q.
(1)求椭圆 的焦点坐标;
的焦点坐标;
(2)求圆Q的方程;
(3)设点 ,过P作圆Q的两条切线分别交椭圆C于点A,B,求
,过P作圆Q的两条切线分别交椭圆C于点A,B,求 的周长.
的周长.
 :
: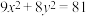 ,直线
,直线 :
: 交椭圆于M,N两点,T为椭圆的右顶点,
交椭圆于M,N两点,T为椭圆的右顶点,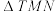 的内切圆为圆Q.
的内切圆为圆Q.(1)求椭圆
 的焦点坐标;
的焦点坐标;(2)求圆Q的方程;
(3)设点
 ,过P作圆Q的两条切线分别交椭圆C于点A,B,求
,过P作圆Q的两条切线分别交椭圆C于点A,B,求 的周长.
的周长.
您最近一年使用:0次
3 . 已知数列 满足
满足 ,
, .
.
(1)求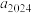 (只需写出数值,不需要证明);
(只需写出数值,不需要证明);
(2)若数列 的通项可以表示成
的通项可以表示成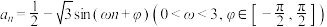 的形式,求
的形式,求 ,
, .
.
 满足
满足 ,
, .
.(1)求
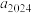 (只需写出数值,不需要证明);
(只需写出数值,不需要证明);(2)若数列
 的通项可以表示成
的通项可以表示成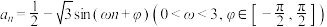 的形式,求
的形式,求 ,
, .
.
您最近一年使用:0次
解题方法
4 . 如图,已知四棱台 中,
中,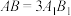 ,
,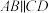 ,
, ,
, ,
,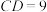 ,
,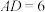 ,且
,且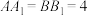 ,
, 为线段
为线段 中点,
中点,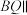 平面
平面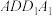 ;
;
(2)若四棱锥 的体积为
的体积为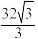 ,求平面
,求平面 与平面
与平面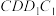 夹角的余弦值.
夹角的余弦值.
 中,
中,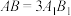 ,
,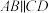 ,
, ,
, ,
,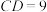 ,
,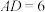 ,且
,且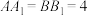 ,
, 为线段
为线段 中点,
中点,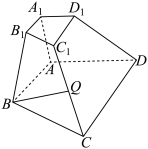
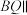 平面
平面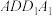 ;
;(2)若四棱锥
 的体积为
的体积为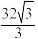 ,求平面
,求平面 与平面
与平面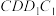 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
5 . 设A,B是两个非空集合,如果对于集合A中的任意一个元素x,按照某种确定的对应关系 ,在集合B中都有唯一确定的元素y和它对应,并且不同的x对应不同的y;同时B中的每一个元素y,都有一个A中的元素x与它对应,则称
,在集合B中都有唯一确定的元素y和它对应,并且不同的x对应不同的y;同时B中的每一个元素y,都有一个A中的元素x与它对应,则称 :
: 为从集合A到集合B的一一对应,并称集合A与B等势,记作
为从集合A到集合B的一一对应,并称集合A与B等势,记作 .若集合A与B之间不存在一一对应关系,则称A与B不等势,记作
.若集合A与B之间不存在一一对应关系,则称A与B不等势,记作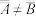 .
.
例如:对于集合 ,
, ,存在一一对应关系
,存在一一对应关系 ,因此
,因此 .
.
(1)已知集合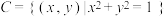 ,
,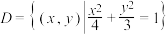 ,试判断
,试判断 是否成立?请说明理由;
是否成立?请说明理由;
(2)证明:① ;
;
② .
.
 ,在集合B中都有唯一确定的元素y和它对应,并且不同的x对应不同的y;同时B中的每一个元素y,都有一个A中的元素x与它对应,则称
,在集合B中都有唯一确定的元素y和它对应,并且不同的x对应不同的y;同时B中的每一个元素y,都有一个A中的元素x与它对应,则称 :
: 为从集合A到集合B的一一对应,并称集合A与B等势,记作
为从集合A到集合B的一一对应,并称集合A与B等势,记作 .若集合A与B之间不存在一一对应关系,则称A与B不等势,记作
.若集合A与B之间不存在一一对应关系,则称A与B不等势,记作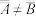 .
.例如:对于集合
 ,
, ,存在一一对应关系
,存在一一对应关系 ,因此
,因此 .
.(1)已知集合
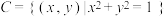 ,
,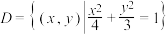 ,试判断
,试判断 是否成立?请说明理由;
是否成立?请说明理由;(2)证明:①
 ;
;②
 .
.
您最近一年使用:0次
2024-04-18更新
|
963次组卷
|
4卷引用:浙江省台州市2024届高三下学期第二次教学质量评估数学试题
浙江省台州市2024届高三下学期第二次教学质量评估数学试题(已下线)压轴题01集合新定义、函数与导数13题型汇总 -1河北省名校联盟2024届高三下学期4月第二次联考数学试题 (已下线)情境10 存在性探索命题
名校
解题方法
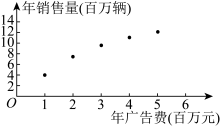
6 . 台州是全国三大电动车生产基地之一,拥有完整的产业链和突出的设计优势.某电动车公司为了抢占更多的市场份额,计划加大广告投入、该公司近5年的年广告费 (单位:百万元)和年销售量
(单位:百万元)和年销售量 (单位:百万辆)关系如图所示:令
(单位:百万辆)关系如图所示:令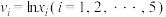 ,数据经过初步处理得:
,数据经过初步处理得:
现有①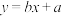 和②
和② 两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.
两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)根据(1)的分析选取拟合程度更好的回归分析模型及表中数据,求出y关于x的回归方程,并预测年广告费为6(百万元)时,产品的年销售量是多少?
(3)该公司生产的电动车毛利润为每辆200元(不含广告费、研发经费).该公司在加大广告投入的同时也加大研发经费的投入,年研发经费为年广告费的199倍.电动车的年净利润受年广告费和年研发经费影响外还受随机变量 影响,设随机变量
影响,设随机变量 服从正态分布
服从正态分布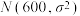 ,且满足
,且满足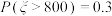 .在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).
.在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).
附:①相关系数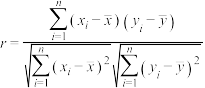 ,
,
回归直线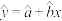 中公式分别为
中公式分别为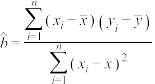 ,
, ;
;
②参考数据: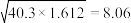 ,
,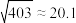 ,
, ,
, .
.
 (单位:百万元)和年销售量
(单位:百万元)和年销售量 (单位:百万辆)关系如图所示:令
(单位:百万辆)关系如图所示:令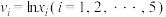 ,数据经过初步处理得:
,数据经过初步处理得:
 | 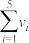 | 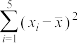 | 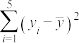 | 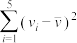 |  |  |
| 44 | 4.8 | 10 | 40.3 | 1.612 | 19.5 | 8.06 |
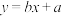 和②
和② 两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.
两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)根据(1)的分析选取拟合程度更好的回归分析模型及表中数据,求出y关于x的回归方程,并预测年广告费为6(百万元)时,产品的年销售量是多少?
(3)该公司生产的电动车毛利润为每辆200元(不含广告费、研发经费).该公司在加大广告投入的同时也加大研发经费的投入,年研发经费为年广告费的199倍.电动车的年净利润受年广告费和年研发经费影响外还受随机变量
 影响,设随机变量
影响,设随机变量 服从正态分布
服从正态分布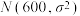 ,且满足
,且满足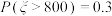 .在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).
.在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).附:①相关系数
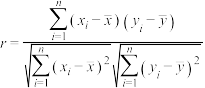 ,
,回归直线
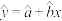 中公式分别为
中公式分别为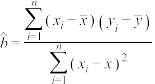 ,
, ;
;②参考数据:
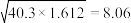 ,
,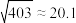 ,
, ,
, .
.
您最近一年使用:0次
2024-04-18更新
|
3019次组卷
|
7卷引用:浙江省台州市2024届高三下学期第二次教学质量评估数学试题
浙江省台州市2024届高三下学期第二次教学质量评估数学试题(已下线)第八章 成对数据的统计分析总结 第一练 考点强化训练(已下线)模块二 专题1统计案例中决策分析问题(北师大高二)(已下线)8.5 二项分布、超几何分布与正态分布(高考真题素材之十年高考)山西省太原市第五中学2023-2024学年高二下学期5月月考数学试题(已下线)专题04 第八章 成对数据的统计分析--高二期末考点大串讲(人教A版2019)湖北省襄阳市第五中学2024届高三下学期第四次适应性测试数学试题
名校
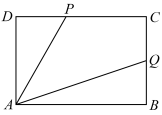
7 . 如图,点P,Q分别是矩形ABCD的边DC,BC上的两点, ,
,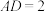 .
. ,
,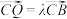 ,
,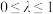 ,求
,求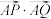 的范围;
的范围;
(2)若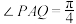 ,求
,求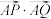 的最小值;
的最小值;
(3)若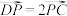 ,连接AP交BC的延长线于点T,Q为BC的中点,试探究线段AB上是否存在一点H,使得
,连接AP交BC的延长线于点T,Q为BC的中点,试探究线段AB上是否存在一点H,使得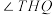 最大.若存在,求BH的长;若不存在,说明理由.
最大.若存在,求BH的长;若不存在,说明理由.
 ,
,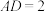 .
.
 ,
,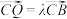 ,
,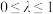 ,求
,求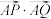 的范围;
的范围;(2)若
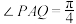 ,求
,求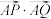 的最小值;
的最小值;(3)若
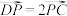 ,连接AP交BC的延长线于点T,Q为BC的中点,试探究线段AB上是否存在一点H,使得
,连接AP交BC的延长线于点T,Q为BC的中点,试探究线段AB上是否存在一点H,使得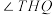 最大.若存在,求BH的长;若不存在,说明理由.
最大.若存在,求BH的长;若不存在,说明理由.
您最近一年使用:0次
2024-03-31更新
|
665次组卷
|
5卷引用:浙江省台州市十校联盟2023-2024学年高一下学期4月期中联考数学试题
浙江省台州市十校联盟2023-2024学年高一下学期4月期中联考数学试题江苏省如皋中学2023-2024学年高一下学期教学质量调研(一)数学试题江苏省连云港市东海高级中学2023-2024学年高一下学期3月教学质量调研数学试题(已下线)模块五 专题6 全真拔高模拟2(高一人教B版期中 )(已下线)模块五 专题6 全真拔高模拟2(苏教版期中研习高一)
名校
8 . 某游乐园中有一座摩天轮.如图所示,摩天轮所在的平面与地面垂直,摩天轮为东西走向.地面上有一条北偏东为 的笔直公路,其中
的笔直公路,其中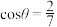 .摩天轮近似为一个圆,其半径为
.摩天轮近似为一个圆,其半径为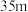 ,圆心
,圆心 到地面的距离为
到地面的距离为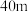 ,其最高点为
,其最高点为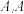 点正下方的地面
点正下方的地面 点与公路的距离为
点与公路的距离为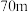 .甲在摩天轮上,乙在公路上.(为了计算方便,甲乙两人的身高、摩天轮的座舱高度和公路宽度忽略不计)
.甲在摩天轮上,乙在公路上.(为了计算方便,甲乙两人的身高、摩天轮的座舱高度和公路宽度忽略不计)
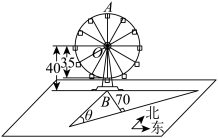
(1)如图所示,甲位于摩天轮的 点处时,从甲看乙的最大俯角的正切值等于多少?
点处时,从甲看乙的最大俯角的正切值等于多少?
(2)当甲随着摩天轮转动时,从乙看甲的最大仰角的正切值等于多少?
 的笔直公路,其中
的笔直公路,其中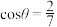 .摩天轮近似为一个圆,其半径为
.摩天轮近似为一个圆,其半径为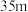 ,圆心
,圆心 到地面的距离为
到地面的距离为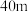 ,其最高点为
,其最高点为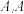 点正下方的地面
点正下方的地面 点与公路的距离为
点与公路的距离为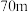 .甲在摩天轮上,乙在公路上.(为了计算方便,甲乙两人的身高、摩天轮的座舱高度和公路宽度忽略不计)
.甲在摩天轮上,乙在公路上.(为了计算方便,甲乙两人的身高、摩天轮的座舱高度和公路宽度忽略不计)
(1)如图所示,甲位于摩天轮的
 点处时,从甲看乙的最大俯角的正切值等于多少?
点处时,从甲看乙的最大俯角的正切值等于多少?(2)当甲随着摩天轮转动时,从乙看甲的最大仰角的正切值等于多少?
您最近一年使用:0次
2024-02-27更新
|
273次组卷
|
3卷引用:浙江省台州市2023-2024学年高二上学期1月期末质量评估数学试题
解题方法
9 . 在长方体 中,
中,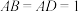 .从①②这两个条件中任选一个解答该题.
.从①②这两个条件中任选一个解答该题.
①直线 与平面
与平面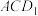 所成角的正弦值为
所成角的正弦值为 ;
;
②平面 与平面
与平面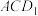 的夹角的余弦值为
的夹角的余弦值为 .
.
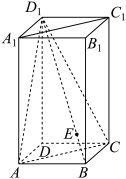
(1)求 的长度;
的长度;
(2) 是线段
是线段 (不含端点)上的一点,若平面
(不含端点)上的一点,若平面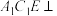 平面
平面 ,求
,求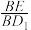 的值.
的值.
 中,
中,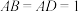 .从①②这两个条件中任选一个解答该题.
.从①②这两个条件中任选一个解答该题.①直线
 与平面
与平面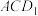 所成角的正弦值为
所成角的正弦值为 ;
;②平面
 与平面
与平面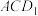 的夹角的余弦值为
的夹角的余弦值为 .
.
(1)求
 的长度;
的长度;(2)
 是线段
是线段 (不含端点)上的一点,若平面
(不含端点)上的一点,若平面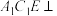 平面
平面 ,求
,求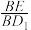 的值.
的值.
您最近一年使用:0次
解题方法
10 . 已知函数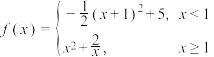 .
.
(1)用单调性定义证明: 在
在 上单调递增;
上单调递增;
(2)若函数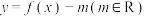 有3个零点
有3个零点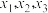 ,满足
,满足 ,且
,且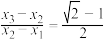 .
.
①求证: ;
;
②求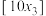 的值(
的值( 表示不超过
表示不超过 的最大整数).
的最大整数).
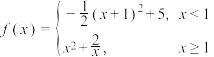 .
.(1)用单调性定义证明:
 在
在 上单调递增;
上单调递增;(2)若函数
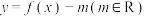 有3个零点
有3个零点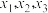 ,满足
,满足 ,且
,且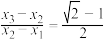 .
.①求证:
 ;
;②求
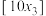 的值(
的值( 表示不超过
表示不超过 的最大整数).
的最大整数).
您最近一年使用:0次



