1 . 已知动点 到点
到点 的距离比到直线
的距离比到直线 的距离小1,设动点
的距离小1,设动点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)已知点 ,过点
,过点 作直线
作直线 与曲线
与曲线 交于
交于 两点,连接
两点,连接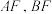 分别交
分别交 于
于 两点.
两点.
①当直线 的斜率存在时,设直线
的斜率存在时,设直线 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,试判断
,试判断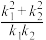 是否为定值?若是,求出该定值;若不是,请说明理由;
是否为定值?若是,求出该定值;若不是,请说明理由;
②求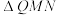 面积的最小值.
面积的最小值.
 到点
到点 的距离比到直线
的距离比到直线 的距离小1,设动点
的距离小1,设动点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的轨迹方程;
的轨迹方程;(2)已知点
 ,过点
,过点 作直线
作直线 与曲线
与曲线 交于
交于 两点,连接
两点,连接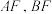 分别交
分别交 于
于 两点.
两点.①当直线
 的斜率存在时,设直线
的斜率存在时,设直线 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,试判断
,试判断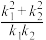 是否为定值?若是,求出该定值;若不是,请说明理由;
是否为定值?若是,求出该定值;若不是,请说明理由;②求
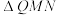 面积的最小值.
面积的最小值.
您最近一年使用:0次
2 . 某高中学校有室内、室外两个运动场.假设同学们可以任意选择其中一个运动场锻炼,也可选择不锻炼,一天最多锻炼一次,一次只能选择一个运动场.若同学们每次锻炼选择去室内、室外运动场的概率均为0.5,每次选择相互独立.设 同学三天内去运动场锻炼的次数为
同学三天内去运动场锻炼的次数为 ,已知
,已知 的分布列如下:(其中
的分布列如下:(其中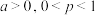 )
)
(1)记事件 表示
表示 同学三天内去运动场锻炼
同学三天内去运动场锻炼 次
次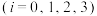 ;事件
;事件 表示
表示 同学在这三天内去室内运动场锻炼的次数大于去室外运动场锻炼的次数.当
同学在这三天内去室内运动场锻炼的次数大于去室外运动场锻炼的次数.当 时,试根据全概率公式求
时,试根据全概率公式求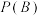 的值;
的值;
(2)是否存在实数 ,使得
,使得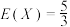 ?若存在,求
?若存在,求 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)记 表示事件“室外运动场举办集体锻炼活动”,
表示事件“室外运动场举办集体锻炼活动”, 表示事件“王同学去室外运动场锻炼”,
表示事件“王同学去室外运动场锻炼”,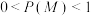 .已知
.已知 同学在室外运动场举办集体锻炼活动的情况下去室外运动场锻炼的概率,比不举办集体锻炼活动的情况下去室外运动场锻炼的概率大,试比较
同学在室外运动场举办集体锻炼活动的情况下去室外运动场锻炼的概率,比不举办集体锻炼活动的情况下去室外运动场锻炼的概率大,试比较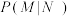 与
与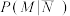 的大小,并证明之.
的大小,并证明之.
 同学三天内去运动场锻炼的次数为
同学三天内去运动场锻炼的次数为 ,已知
,已知 的分布列如下:(其中
的分布列如下:(其中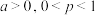 )
) | 0 | 1 | 2 | 3 |
 | 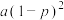 | 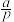 |  |  |
 表示
表示 同学三天内去运动场锻炼
同学三天内去运动场锻炼 次
次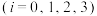 ;事件
;事件 表示
表示 同学在这三天内去室内运动场锻炼的次数大于去室外运动场锻炼的次数.当
同学在这三天内去室内运动场锻炼的次数大于去室外运动场锻炼的次数.当 时,试根据全概率公式求
时,试根据全概率公式求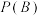 的值;
的值;(2)是否存在实数
 ,使得
,使得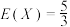 ?若存在,求
?若存在,求 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(3)记
 表示事件“室外运动场举办集体锻炼活动”,
表示事件“室外运动场举办集体锻炼活动”, 表示事件“王同学去室外运动场锻炼”,
表示事件“王同学去室外运动场锻炼”,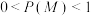 .已知
.已知 同学在室外运动场举办集体锻炼活动的情况下去室外运动场锻炼的概率,比不举办集体锻炼活动的情况下去室外运动场锻炼的概率大,试比较
同学在室外运动场举办集体锻炼活动的情况下去室外运动场锻炼的概率,比不举办集体锻炼活动的情况下去室外运动场锻炼的概率大,试比较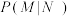 与
与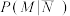 的大小,并证明之.
的大小,并证明之.
您最近一年使用:0次
名校
解题方法
3 . 如图,对于曲线 ,若存在圆
,若存在圆 满足如下条件:
满足如下条件:
①圆 与曲线
与曲线 有公共点
有公共点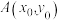 ,且圆心在曲线
,且圆心在曲线 凹的一侧;
凹的一侧;
②圆 与曲线
与曲线 在点
在点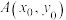 处有相同的切线;
处有相同的切线;
③曲线 的导函数在
的导函数在 处的导数(即曲线
处的导数(即曲线 在点
在点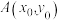 的二阶导数)等于圆
的二阶导数)等于圆 在点
在点 处的二阶导数(已知圆
处的二阶导数(已知圆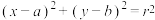 在点
在点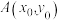 处的二阶导数等于
处的二阶导数等于 );则称圆
);则称圆 为曲线
为曲线 在
在 点处的曲率圆,其半径
点处的曲率圆,其半径 称为曲率半径.
称为曲率半径.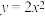 在原点的曲率圆的方程;
在原点的曲率圆的方程;
(2)(i)求证:平面曲线 在点
在点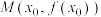 的曲率半径为
的曲率半径为 (其中
(其中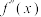 表示
表示 的导函数);
的导函数);
(ii)若圆 为函数
为函数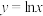 的一个曲率圆,求圆
的一个曲率圆,求圆 半径的最小值;
半径的最小值;
(3)若曲线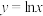 在
在 处有相同的曲率半径,求证:
处有相同的曲率半径,求证: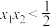 .
.
 ,若存在圆
,若存在圆 满足如下条件:
满足如下条件:①圆
 与曲线
与曲线 有公共点
有公共点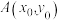 ,且圆心在曲线
,且圆心在曲线 凹的一侧;
凹的一侧;②圆
 与曲线
与曲线 在点
在点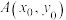 处有相同的切线;
处有相同的切线;③曲线
 的导函数在
的导函数在 处的导数(即曲线
处的导数(即曲线 在点
在点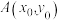 的二阶导数)等于圆
的二阶导数)等于圆 在点
在点 处的二阶导数(已知圆
处的二阶导数(已知圆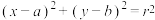 在点
在点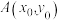 处的二阶导数等于
处的二阶导数等于 );则称圆
);则称圆 为曲线
为曲线 在
在 点处的曲率圆,其半径
点处的曲率圆,其半径 称为曲率半径.
称为曲率半径.
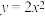 在原点的曲率圆的方程;
在原点的曲率圆的方程;(2)(i)求证:平面曲线
 在点
在点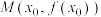 的曲率半径为
的曲率半径为 (其中
(其中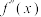 表示
表示 的导函数);
的导函数);(ii)若圆
 为函数
为函数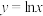 的一个曲率圆,求圆
的一个曲率圆,求圆 半径的最小值;
半径的最小值;(3)若曲线
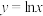 在
在 处有相同的曲率半径,求证:
处有相同的曲率半径,求证: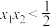 .
.
您最近一年使用:0次
名校
4 . 18世纪早期英国牛顿学派最优秀代表人物之一的数学家泰勒(Brook Taylor)发现的泰勒公式(又称夌克劳林公式)有如下特殊形式:当 在
在 处的
处的 阶导数都存在时,
阶导数都存在时,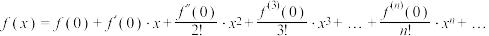 .其中,
.其中, 表示
表示 的二阶导数,即为
的二阶导数,即为 的导数,
的导数,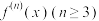 表示
表示 的
的 阶导数.
阶导数.
(1)根据公式估计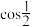 的值;(结果保留两位有效数字)
的值;(结果保留两位有效数字)
(2)由公式可得: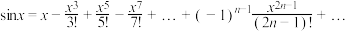 ,当
,当 时,请比较
时,请比较 与
与 的大小,并给出证明;
的大小,并给出证明;
(3)已知 ,证明:
,证明: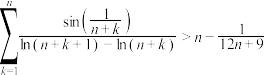 .
.
 在
在 处的
处的 阶导数都存在时,
阶导数都存在时,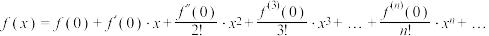 .其中,
.其中, 表示
表示 的二阶导数,即为
的二阶导数,即为 的导数,
的导数,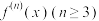 表示
表示 的
的 阶导数.
阶导数.(1)根据公式估计
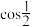 的值;(结果保留两位有效数字)
的值;(结果保留两位有效数字)(2)由公式可得:
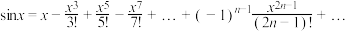 ,当
,当 时,请比较
时,请比较 与
与 的大小,并给出证明;
的大小,并给出证明;(3)已知
 ,证明:
,证明: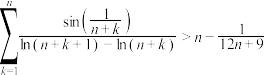 .
.
您最近一年使用:0次
5 . 对于函数 的导函数
的导函数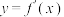 ,若在其定义域内存在实数
,若在其定义域内存在实数 和
和 ,使得
,使得 成立,则称
成立,则称 是“跃然”函数,并称
是“跃然”函数,并称 是函数
是函数 的“跃然值”.
的“跃然值”.
(1)证明:当 时,函数
时,函数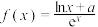 是“跃然”函数;
是“跃然”函数;
(2)证明: 为“跃然”函数,并求出该函数“跃然值”的取值范围.
为“跃然”函数,并求出该函数“跃然值”的取值范围.
 的导函数
的导函数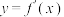 ,若在其定义域内存在实数
,若在其定义域内存在实数 和
和 ,使得
,使得 成立,则称
成立,则称 是“跃然”函数,并称
是“跃然”函数,并称 是函数
是函数 的“跃然值”.
的“跃然值”.(1)证明:当
 时,函数
时,函数 是“跃然”函数;
是“跃然”函数;(2)证明:
 为“跃然”函数,并求出该函数“跃然值”的取值范围.
为“跃然”函数,并求出该函数“跃然值”的取值范围.
您最近一年使用:0次
名校
解题方法
6 . 已知函数 .
.
(1)求函数 的最小值;
的最小值;
(2)求函数 在
在 上的最小值;
上的最小值;
(3)若不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)求函数
 的最小值;
的最小值;(2)求函数
 在
在 上的最小值;
上的最小值;(3)若不等式
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-04-30更新
|
671次组卷
|
2卷引用:湖北省部分省级示范高中2023-2024学年高二下学期4月期中测试数学试题
7 . 已知动点M到点 的距离与到直线
的距离与到直线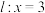 的距离之比为
的距离之比为 .
.
(1)求动点M的轨迹C的方程;
(2)过点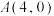 的直线与轨迹C交于P,Q两点,点P关于x轴对称的点为R,求
的直线与轨迹C交于P,Q两点,点P关于x轴对称的点为R,求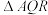 面积的取值范围.
面积的取值范围.
 的距离与到直线
的距离与到直线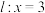 的距离之比为
的距离之比为 .
.(1)求动点M的轨迹C的方程;
(2)过点
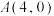 的直线与轨迹C交于P,Q两点,点P关于x轴对称的点为R,求
的直线与轨迹C交于P,Q两点,点P关于x轴对称的点为R,求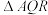 面积的取值范围.
面积的取值范围.
您最近一年使用:0次
名校
8 . 帕德近似是法国数学家亨利·帕德发明的用有理多项式近似特定函数的方法.给定两个正整数 ,
, ,函数
,函数 在
在 处的
处的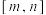 阶帕德近似定义为:
阶帕德近似定义为: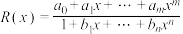 ,且满足:
,且满足: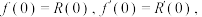
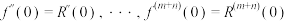 .(注:
.(注: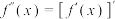 ,
,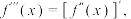
 为
为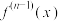 的导数)已知
的导数)已知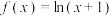 在
在 处的
处的 阶帕德近似为
阶帕德近似为 .
.
(1)求实数 的值;
的值;
(2)证明:当 时,
时, ;
;
(3)设 为实数,讨论方程
为实数,讨论方程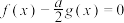 的解的个数.
的解的个数.
 ,
, ,函数
,函数 在
在 处的
处的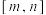 阶帕德近似定义为:
阶帕德近似定义为: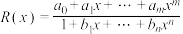 ,且满足:
,且满足: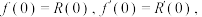
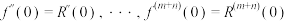 .(注:
.(注: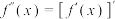 ,
,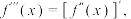
 为
为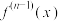 的导数)已知
的导数)已知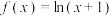 在
在 处的
处的 阶帕德近似为
阶帕德近似为 .
.(1)求实数
 的值;
的值;(2)证明:当
 时,
时, ;
;(3)设
 为实数,讨论方程
为实数,讨论方程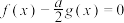 的解的个数.
的解的个数.
您最近一年使用:0次
名校
9 . 已知函数 和
和 的定义域分别为
的定义域分别为 和
和 ,若对任意
,若对任意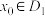 ,恰好存在
,恰好存在 个不同的实数
个不同的实数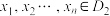 ,使得
,使得 (其中
(其中 ),则称
),则称 为
为 的“
的“ 重覆盖函数”.
重覆盖函数”.
(1)试判断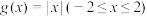 是否为
是否为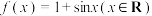 的“2重覆盖函数”?请说明理由;
的“2重覆盖函数”?请说明理由;
(2)若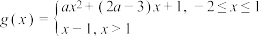 ,为
,为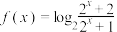 ,的“2重覆盖函数”,求实数
,的“2重覆盖函数”,求实数 的取值范围;
的取值范围;
(3)函数 表示不超过
表示不超过 的最大整数,如
的最大整数,如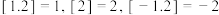 .若
.若 为
为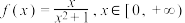 的“2024重覆盖函数”请直接写出正实数
的“2024重覆盖函数”请直接写出正实数 的取值范围.
的取值范围.
 和
和 的定义域分别为
的定义域分别为 和
和 ,若对任意
,若对任意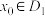 ,恰好存在
,恰好存在 个不同的实数
个不同的实数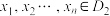 ,使得
,使得 (其中
(其中 ),则称
),则称 为
为 的“
的“ 重覆盖函数”.
重覆盖函数”.(1)试判断
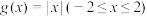 是否为
是否为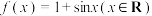 的“2重覆盖函数”?请说明理由;
的“2重覆盖函数”?请说明理由;(2)若
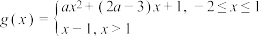 ,为
,为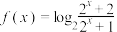 ,的“2重覆盖函数”,求实数
,的“2重覆盖函数”,求实数 的取值范围;
的取值范围;(3)函数
 表示不超过
表示不超过 的最大整数,如
的最大整数,如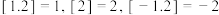 .若
.若 为
为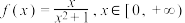 的“2024重覆盖函数”请直接写出正实数
的“2024重覆盖函数”请直接写出正实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-03-29更新
|
248次组卷
|
2卷引用:湖北省鄂西南三校2023-2024学年高二下学期三月联考数学试卷
10 . 相传古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究数,并根据小石子所排列的形状把数分成许多类.现有三角形数表按如图的方式构成,其中项数 :第一行是以1为首项,2为公差的等差数列.从第二行起,每一个数是其肩上两个数的和,例如:
:第一行是以1为首项,2为公差的等差数列.从第二行起,每一个数是其肩上两个数的和,例如: ;
;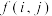 为数表中第
为数表中第 行的第
行的第 个数.
个数.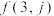 和
和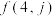 ;
;
(2)一般地,证明一个与正整数 有关的命题,可按下列步骤进行:①证明当
有关的命题,可按下列步骤进行:①证明当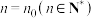 时命题成立;②以“当
时命题成立;②以“当 时命题成立”为条件,推出“当
时命题成立”为条件,推出“当 时命题也成立.”完成这两个步骤就可以断定命题对
时命题也成立.”完成这两个步骤就可以断定命题对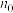 开始的所有正整数
开始的所有正整数 都成立,这种方法即数学归纳法.请证明:数表中除最后2行外每一行的数都依次成等差数列,并求
都成立,这种方法即数学归纳法.请证明:数表中除最后2行外每一行的数都依次成等差数列,并求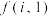 关于
关于 的表达式;
的表达式;
(3)若 ,
,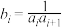 ,试求一个等比数列
,试求一个等比数列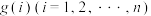 ,使得
,使得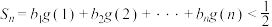 ,且对于任意的
,且对于任意的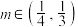 ,均存在实数
,均存在实数 ,当
,当 时,都有
时,都有 .
.
 :第一行是以1为首项,2为公差的等差数列.从第二行起,每一个数是其肩上两个数的和,例如:
:第一行是以1为首项,2为公差的等差数列.从第二行起,每一个数是其肩上两个数的和,例如: ;
;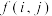 为数表中第
为数表中第 行的第
行的第 个数.
个数.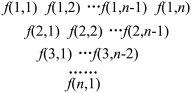
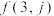 和
和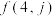 ;
;(2)一般地,证明一个与正整数
 有关的命题,可按下列步骤进行:①证明当
有关的命题,可按下列步骤进行:①证明当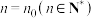 时命题成立;②以“当
时命题成立;②以“当 时命题成立”为条件,推出“当
时命题成立”为条件,推出“当 时命题也成立.”完成这两个步骤就可以断定命题对
时命题也成立.”完成这两个步骤就可以断定命题对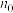 开始的所有正整数
开始的所有正整数 都成立,这种方法即数学归纳法.请证明:数表中除最后2行外每一行的数都依次成等差数列,并求
都成立,这种方法即数学归纳法.请证明:数表中除最后2行外每一行的数都依次成等差数列,并求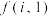 关于
关于 的表达式;
的表达式;(3)若
 ,
,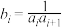 ,试求一个等比数列
,试求一个等比数列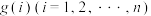 ,使得
,使得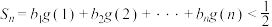 ,且对于任意的
,且对于任意的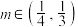 ,均存在实数
,均存在实数 ,当
,当 时,都有
时,都有 .
.
您最近一年使用:0次
2024-03-06更新
|
347次组卷
|
2卷引用:湖北省云学名校联盟2023-2024学年高二下学期3月联考数学试卷



