名校
1 . 随机变量 且
且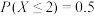 ,随机变量
,随机变量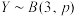 ,若
,若 ,则( )
,则( )
 且
且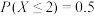 ,随机变量
,随机变量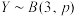 ,若
,若 ,则( )
,则( )A. | B.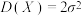 | C. | D.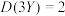 |
您最近一年使用:0次
2024-03-26更新
|
518次组卷
|
11卷引用:福建省厦门外国语学校2023届高三适应性考试数学试题
福建省厦门外国语学校2023届高三适应性考试数学试题山东省泰安市2023届高三二模数学试题辽宁省实验中学2023届高三第四次模拟考试数学试卷(已下线)模块三 专题2 小题进阶提升练( 2)(北师大2019版 高二)(已下线)模块三 专题2 小题进阶提升练( 2)(苏教版高二)广东省茂名市第一中学2023届高三下学期5月第二次半月考数学试题浙江省嘉兴市秀水高级中学2022-2023学年高二下学期5月月考数学试题江苏省靖江中学、华罗庚中学2023-2024学年高三上学期第一次阶段考试数学试题山东省潍坊市昌乐北大公学学校2024届高三下学期3月监测数学试题(已下线)7.5正态分布 第三练 能力提升拔高(已下线)专题3.4正态分布(五个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
2 . 如图,在棱长为4的正方体 中,E,F,G分别为棱
中,E,F,G分别为棱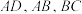 的中点,点P为线段
的中点,点P为线段 上的动点(包含端点),则( )
上的动点(包含端点),则( )
 中,E,F,G分别为棱
中,E,F,G分别为棱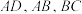 的中点,点P为线段
的中点,点P为线段 上的动点(包含端点),则( )
上的动点(包含端点),则( )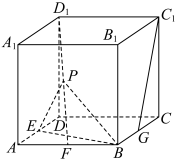
A.存在点P,使得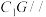 平面 平面 | B.对任意点P,平面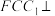 平面 平面 |
C.两条异面直线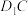 和 和 所成的角为 所成的角为 | D.点 到直线 到直线 的距离为4 的距离为4 |
您最近一年使用:0次
2024-03-06更新
|
831次组卷
|
15卷引用:福建省厦门双十中学2023届高三高考适应性考试数学试题
福建省厦门双十中学2023届高三高考适应性考试数学试题湖北省七市(州)2023届高三下学期3月联合统一调研测试数学试题黑龙江省大庆铁人中学2022-2023学年高三第二次模拟考试数学试题江苏省南京市第五高级中学2023届高三二模热身测试数学试题(已下线)8.6 空间直线、平面的垂直(分层练习)-2022-2023学年高一数学同步精品课堂(人教A版2019必修第二册)广西南宁市第二中学2022-2023学年高二下学期期末考试数学试题辽宁省大连市滨城高中联盟2023-2024学年高二上学期10月月考数学试题福建省龙岩市第一中学2024届高三上学期第三次月考数学试题(已下线)浙江省绍兴市上虞区2022-2023学年高一下学期期末质量调研卷数学试题浙江省杭州学军中学紫金港校区2023-2024学年高二上学期期末数学试题(已下线)第四章 立体几何解题通法 专题五 平移变换法 微点3 平移变换法综合训练【培优版】(已下线)第八章立体几何初步(单元测试)-【上好课】-(人教A版2019必修第二册)浙江省余姚中学2023-2024学年高一下学期期中考试数学试题(已下线)难度1 小题强化限时晋级练(高一期末题型专项)江苏省南京市第五高级中学2023-2024学年高二下学期期末调研数学试卷
名校
解题方法
3 . 不等式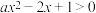 (
( )恒成立的一个充分不必要条件是( )
)恒成立的一个充分不必要条件是( )
A. | B. | C. | D.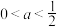 |
您最近一年使用:0次
2024-01-18更新
|
566次组卷
|
12卷引用:福建省厦门市2023届高三下学期第二次质量检测数学试题
福建省厦门市2023届高三下学期第二次质量检测数学试题福建省厦门双十中学2024届高三上学期9月基础测试数学试题(已下线)第二章 一元二次函数、方程和不等式 讲核心 02(已下线)专题06 不等式(已下线)专题01 集合与常用逻辑用语福建省福州市鼓山中学2023届高三下学期3月月考数学试题江西省宜春市宜丰县宜丰中学2022-2023学年高二下学期期中数学试题新疆霍城县江苏中学2024届高三上学期开学摸底考试数学试题新疆维吾尔自治区伊犁州伊宁市第一中学2024届高三上学期10月月考数学试题重庆市第七中学校2024届高三上学期第一次月考数学试题(已下线)考点8 一元二次方程、不等式 --2024届高考数学考点总动员【练】(已下线)FHsx1225yl139
名校
4 . 平面上的三个力 ,
, ,
, 作用于同一点,且处于平衡状态.已知
作用于同一点,且处于平衡状态.已知 ,
,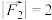 ,
,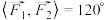 ,则
,则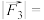 ( )
( )
 ,
, ,
, 作用于同一点,且处于平衡状态.已知
作用于同一点,且处于平衡状态.已知 ,
,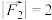 ,
,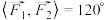 ,则
,则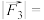 ( )
( )A. | B.1 | C. | D.2 |
您最近一年使用:0次
2024-01-06更新
|
322次组卷
|
7卷引用:福建省厦门市2023届高三毕业班第四次质量检测数学试题
福建省厦门市2023届高三毕业班第四次质量检测数学试题辽宁省沈阳市翔宇中学2022-2023学年高一下学期第二次月考测试数学试题(已下线)第四节 平面向量的综合应用 B素养提升卷江苏省2024届高三上学期期末迎考数学试题(已下线)专题07 向量的应用-【寒假自学课】(苏教版2019)(已下线)9.4 向量应用-【帮课堂】(苏教版2019必修第二册)(已下线)6.3.5平面向量数量积的坐标表示(导学案) -【上好课】
名校
解题方法
5 . 法国数学家庞加莱是个喜欢吃面包的人,他每天都会到同一家面包店购买一个面包.该面包店的面包师声称自己所出售的面包的平均质量是1 000 g,上下浮动不超过50 g.这句话用数学语言来表达就是:每个面包的质量服从期望为1 000 g,标准差为50 g的正态分布.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N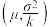 .利用该结论解决下面问题.
.利用该结论解决下面问题.
①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N
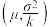 .利用该结论解决下面问题.
.利用该结论解决下面问题.①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
您最近一年使用:0次
2024-03-21更新
|
398次组卷
|
21卷引用:福建省厦门第一中学2023届高三二模数学试题
福建省厦门第一中学2023届高三二模数学试题江苏省扬州中学2023届高三下学期阶段测试数学试题江苏省盐城市伍佑中学2023届高三高考热身考试数学试题辽宁省大连市第八中学2023届高考适应性测试数学试题浙江省杭州第二中学2023届高三下学期3月月考数学试题江苏省常州市溧阳中学2022-2023学年高二下学期4月阶段性调研测试数学试题河北省保定市六校联盟2022-2023学年高二下学期4月联考数学试题(已下线)8.3 正态分布-【题型分类归纳】2022-2023学年高二数学同步讲与练(苏教版2019选择性必修第二册)辽宁省锦州市某校2023-2024学年高三上学期第二次考试数学试题(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-3山东省青岛市四区2021-2022学年高三上学期期末考试数学试题福建省尤溪第一中学2021~2022学年高二下学期数学期末模拟卷(三)试题湖南省长沙市雅礼中学2022-2023学年高三上学期月考(五)数学试题山东省青岛市4区县2021-2022学年高三上学期期末考试数学试题(已下线)专题04 超几何分布+二项分布+正态分布压轴题(3)(已下线)第八章 概率(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第七章:随机变量及其分布章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)黑龙江省牡丹江市第一高级中学2023-2024学年高二下学期5月期中考试数学试题(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)
名校
6 . 已知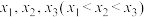 是函数
是函数 (
(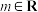 且
且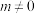 )的三个零点,则
)的三个零点,则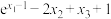 的可能取值有( )
的可能取值有( )
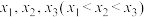 是函数
是函数 (
(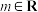 且
且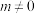 )的三个零点,则
)的三个零点,则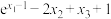 的可能取值有( )
的可能取值有( )| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
2023-10-05更新
|
511次组卷
|
2卷引用:福建省厦门第一中学2023届高三四模数学试题
名校
7 . 某商场举行抽奖活动,箱子里有10个大小一样的小球,其中红色的5个,黄色的3个,蓝色的2个,现从中任意取出3个,则其中至少含有两种不同颜色的小球的概率为__________ .
您最近一年使用:0次
2023-09-27更新
|
1471次组卷
|
5卷引用:福建省厦门第一中学2023届高三四模数学试题
福建省厦门第一中学2023届高三四模数学试题广西名校2024届高三下学期高考模拟试卷数学信息卷(已下线)考点巩固卷24 古典概型、相互独立、条件概率及全概率公式(七大考点)(已下线)第04讲 随机事件、频率与概率(六大题型)(讲义)(已下线)第05讲 古典概型与概率的基本性质(练习)
名校
解题方法
8 . 已知角 的终边落在直线
的终边落在直线 上,则
上,则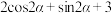 的值为( )
的值为( )
 的终边落在直线
的终边落在直线 上,则
上,则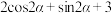 的值为( )
的值为( )A. | B.1 | C.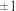 | D. |
您最近一年使用:0次
名校
解题方法
9 . 已知 为双曲线
为双曲线 :
: 的右焦点,平行于
的右焦点,平行于 轴的直线
轴的直线 分别交
分别交 的渐近线和右支于点
的渐近线和右支于点 ,
, ,且
,且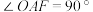 ,
, ,则
,则 的离心率为( )
的离心率为( )
 为双曲线
为双曲线 :
: 的右焦点,平行于
的右焦点,平行于 轴的直线
轴的直线 分别交
分别交 的渐近线和右支于点
的渐近线和右支于点 ,
, ,且
,且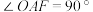 ,
, ,则
,则 的离心率为( )
的离心率为( )A.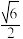 | B. | C. | D. |
您最近一年使用:0次
2023-09-27更新
|
1518次组卷
|
8卷引用:福建省厦门第一中学2023届高三四模数学试题
福建省厦门第一中学2023届高三四模数学试题(已下线)模块一 专题3 圆锥曲线的方程(人教A)(1)(已下线)重难点突破04 轻松搞定圆锥曲线离心率十九大模型(十九大题型)-4(已下线)3.2.2 双曲线的简单的几何性质(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)(已下线)3.2.2 双曲线的简单的几何性质(重难点突破)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)(已下线)专题11 圆锥曲线(4大易错点分析+解题模板+举一反三+易错题通关)(已下线)第02讲 3.2双曲线(3)(已下线)专题25 双曲线的简单几何性质9种常见考法归类(1)
名校
解题方法
10 . 已知直线 :
: 关于直线
关于直线 的对称直线为
的对称直线为 轴,则
轴,则 的方程为
的方程为___________ .
 :
: 关于直线
关于直线 的对称直线为
的对称直线为 轴,则
轴,则 的方程为
的方程为
您最近一年使用:0次



