名校
1 . 已知函数 ,
,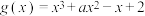
(1)求函数 的单调区间;
的单调区间;
(2)若对一切的 ,
,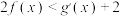 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 ,
,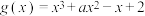
(1)求函数
 的单调区间;
的单调区间;(2)若对一切的
 ,
,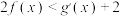 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-05-18更新
|
810次组卷
|
21卷引用:2015-2016学年湖北省襄阳市白水高中高二下3月月考文科数学试卷
2015-2016学年湖北省襄阳市白水高中高二下3月月考文科数学试卷(已下线)2014年高考数学(理)二轮复习体系通关训练倒数第9天练习卷2016届山东省实验中学高三上第二次诊考文科数学试卷2015-2016学年河南省驻马店市高二上学期期末文科数学试卷2015-2016学年河南省驻马店市高二上学期期末理科数学试卷湖北省宜昌市七校教学协作体2016-2017学年高二下学期期末考试数学(文)试题黑龙江省伊春市第二中学2016-2017学年高二下学期期中考试数学(文)试题安徽省合肥市肥东县第二中学2019-2020学年高二(共建班)下学期期中数学(文)试题重庆市凤鸣山中学2019-2020学年高二下学期6月月考数学试题(已下线)专题3.5 高考解答题热点题型(二)利用导数解决不等式恒(能)成立问题-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破(已下线)专题3.5 高考解答题热点题型(二)利用导数解决不等式恒(能)成立问题-2021年高考数学(文)一轮复习-题型全归纳与高效训练突破山西省运城市临晋中学2019-2020学年高二下学期期末数学(理)试题黑龙江省八校2020-2021学年高三摸底考试数学(文)试题黑龙江省八校2020-2021学年高三摸底考试数学(理)试题湖南省邵阳市新邵县2020-2021学年高二上学期期末数学试题陕西省榆林市绥德中学2022-2023学年高二下学期第一次阶段测试理科数学试题陕西省榆林市绥德中学2022-2023学年高二下学期第一次阶段测试文科数学试题江苏省盐城市大丰区南阳中学2022-2023学年高二下学期5月月考数学试题广东省清远市“四校联盟”2022-2023学年高二下学期期中数学试题(已下线)第六章 导数与不等式恒成立问题 专题六 单变量恒成立之参变分离法 微点1 单变量恒成立之参变分离后导函数零点可求、可猜、不可求型专题05导数及其应用(第三部分)
名校
2 . 已知 ,设函数
,设函数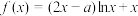 ,
, 是
是 的导函数.
的导函数.
(1)若 ,求曲线
,求曲线 在点
在点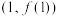 处的切线方程;
处的切线方程;
(2)若 在区间
在区间 上存在两个不同的零点
上存在两个不同的零点 ,
,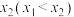 .
.
①求实数 的取值范围;
的取值范围;
②证明: .
.
 ,设函数
,设函数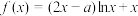 ,
, 是
是 的导函数.
的导函数.(1)若
 ,求曲线
,求曲线 在点
在点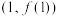 处的切线方程;
处的切线方程;(2)若
 在区间
在区间 上存在两个不同的零点
上存在两个不同的零点 ,
,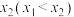 .
.①求实数
 的取值范围;
的取值范围;②证明:
 .
.
您最近一年使用:0次
2023-05-14更新
|
952次组卷
|
7卷引用:湖北省襄阳市第四中学2023届高三下学期5月适应性考试(二)数学试题
湖北省襄阳市第四中学2023届高三下学期5月适应性考试(二)数学试题福建省厦门双十中学2023届高三热身考试数学试题新疆生产建设兵团第三师图木舒克市第一中学2024届高三上学期11月月考数学试题(已下线)专题19 导数综合-2河南省郑州市宇华实验学校2024届高三上学期期末数学试题(已下线)专题3 导数与函数的零点(方程的根)【讲】(已下线)专题8 导数与拐点偏移【讲】
3 . 如果一个复数的实部和虚部相等,则称这个复数为“等部复数”,若复数 (i为虚数单位)为“等部复数”,则实数a的值为( )
(i为虚数单位)为“等部复数”,则实数a的值为( )
 (i为虚数单位)为“等部复数”,则实数a的值为( )
(i为虚数单位)为“等部复数”,则实数a的值为( )A. | B. | C.0 | D.1 |
您最近一年使用:0次
2023-04-30更新
|
1073次组卷
|
6卷引用:湖北省襄阳市第三中学2022-2023学年高一下学期5月月考数学试题
名校
4 . 若 ,
,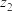 是方程
是方程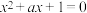 的两个虚数根,则( )
的两个虚数根,则( )
 ,
,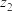 是方程
是方程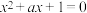 的两个虚数根,则( )
的两个虚数根,则( )A. 的取值范围为 的取值范围为 | B. 的共轭复数是 的共轭复数是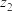 |
C. | D.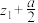 为纯虚数 为纯虚数 |
您最近一年使用:0次
2023-04-26更新
|
942次组卷
|
11卷引用:湖北省襄阳市第三中学2022-2023学年高一下学期5月月考数学试题
湖北省襄阳市第三中学2022-2023学年高一下学期5月月考数学试题山东省部分学校2022-2023学年高一下学期期中质量监测联合调考数学试题四川省德阳市德阳中学校2022-2023学年高一下学期5月月考数学试题(已下线)模块二 专题3 《复数》单元检测篇 B提升卷 (北师大版)(已下线)模块二 专题2 《复数》单元检测篇 B提升卷(已下线)模块二 专题4 复数 单元检测篇 B基础卷(人教B)(已下线)模块二《复数》单元检测篇 B基础卷 (北师大版)福建省福州市闽侯县第一中学2022-2023学年高一下学期5月月考数学试题山东省聊城市2022-2023学年高一下学期3月质量监测数学试题山东省泰安肥城市2022-2023学年高一下学期期中考试数学试题江西省部分学校2022-2023学年高一下学期5月月考模拟数学试题
名校
5 . 在①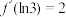 ;②
;② 的图象在点
的图象在点 处的切线斜率为0;③
处的切线斜率为0;③ 的递减区间为
的递减区间为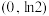 ,这三个条件中任选一个补充在下面的问题(1)中,并加以解答.
,这三个条件中任选一个补充在下面的问题(1)中,并加以解答.
已知 .
.
(1)若_________,求实数a的值;(注:如果选择多个条件分别解答,按第一个解答计分.)
(2)若 ,讨论函数
,讨论函数 的单调性.
的单调性.
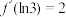 ;②
;② 的图象在点
的图象在点 处的切线斜率为0;③
处的切线斜率为0;③ 的递减区间为
的递减区间为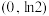 ,这三个条件中任选一个补充在下面的问题(1)中,并加以解答.
,这三个条件中任选一个补充在下面的问题(1)中,并加以解答.已知
 .
.(1)若_________,求实数a的值;(注:如果选择多个条件分别解答,按第一个解答计分.)
(2)若
 ,讨论函数
,讨论函数 的单调性.
的单调性.
您最近一年使用:0次
名校
解题方法
6 . 已知函数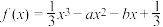 在
在 时有极大值2.
时有极大值2.
(1)求常数a,b的值;
(2)求 在区间
在区间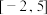 上的最值.
上的最值.
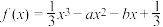 在
在 时有极大值2.
时有极大值2.(1)求常数a,b的值;
(2)求
 在区间
在区间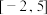 上的最值.
上的最值.
您最近一年使用:0次
名校
解题方法
7 . 函数 恰有3个单调区间的充分不必要条件是( )
恰有3个单调区间的充分不必要条件是( )
 恰有3个单调区间的充分不必要条件是( )
恰有3个单调区间的充分不必要条件是( )A. | B.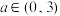 | C.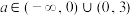 | D. |
您最近一年使用:0次
2023-04-15更新
|
708次组卷
|
2卷引用:湖北省鄂西北六校(宜城一中、枣阳一中等六校)2022-2023学年高二下学期期中联考数学试题
8 . 设 是函数
是函数 的导数,
的导数,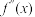 是
是 的导数,若方程
的导数,若方程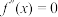 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”.已知:任何三次函数既有拐点,又有对称中心,且拐点就是对称中心.设
的“拐点”.已知:任何三次函数既有拐点,又有对称中心,且拐点就是对称中心.设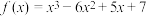 ,数列
,数列 的通项公式为
的通项公式为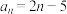 ,则
,则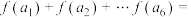 ( )
( )
 是函数
是函数 的导数,
的导数,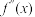 是
是 的导数,若方程
的导数,若方程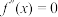 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”.已知:任何三次函数既有拐点,又有对称中心,且拐点就是对称中心.设
的“拐点”.已知:任何三次函数既有拐点,又有对称中心,且拐点就是对称中心.设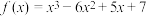 ,数列
,数列 的通项公式为
的通项公式为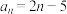 ,则
,则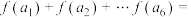 ( )
( )| A.8 | B.7 | C.6 | D.5 |
您最近一年使用:0次
名校
解题方法
9 . 函数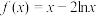 的单调递增区间是( )
的单调递增区间是( )
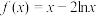 的单调递增区间是( )
的单调递增区间是( )A. | B.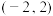 | C. | D. |
您最近一年使用:0次
2023-04-15更新
|
905次组卷
|
3卷引用:湖北省鄂西北六校(宜城一中、枣阳一中等六校)2022-2023学年高二下学期期中联考数学试题
名校
10 . 如果曲线 存在相互垂直的两条切线,称函数
存在相互垂直的两条切线,称函数 是“正交函数”.已知
是“正交函数”.已知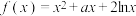 ,设曲线
,设曲线 在点
在点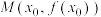 处的切线为
处的切线为 .
.
(1)当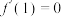 时,求实数
时,求实数 的值;
的值;
(2)当 ,
,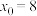 时,是否存在直线
时,是否存在直线 满足
满足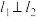 ,且
,且 与曲线
与曲线 相切?请说明理由;
相切?请说明理由;
(3)当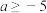 时,如果函数
时,如果函数 是“正交函数”,求满足要求的实数
是“正交函数”,求满足要求的实数 的集合
的集合 ;若对任意
;若对任意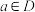 ,曲线
,曲线 都不存在与
都不存在与 垂直的切线
垂直的切线 ,求
,求 的取值范围.
的取值范围.
 存在相互垂直的两条切线,称函数
存在相互垂直的两条切线,称函数 是“正交函数”.已知
是“正交函数”.已知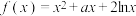 ,设曲线
,设曲线 在点
在点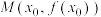 处的切线为
处的切线为 .
.(1)当
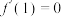 时,求实数
时,求实数 的值;
的值;(2)当
 ,
,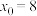 时,是否存在直线
时,是否存在直线 满足
满足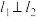 ,且
,且 与曲线
与曲线 相切?请说明理由;
相切?请说明理由;(3)当
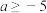 时,如果函数
时,如果函数 是“正交函数”,求满足要求的实数
是“正交函数”,求满足要求的实数 的集合
的集合 ;若对任意
;若对任意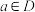 ,曲线
,曲线 都不存在与
都不存在与 垂直的切线
垂直的切线 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-04-14更新
|
964次组卷
|
5卷引用:湖北省襄阳市第五中学2023届高三下学期适应性考试(一)数学试题
湖北省襄阳市第五中学2023届高三下学期适应性考试(一)数学试题上海市闵行区2023届高三二模数学试题(已下线)专题03 导数及其应用(已下线)专题02 函数及其应用(已下线)专题08 平面解析几何-学易金卷



