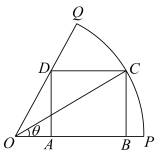
1 . 已知OPQ是半径为1,圆心角为 的扇形,C是扇形弧上的动点.ABCD是扇形的内接矩形,记
的扇形,C是扇形弧上的动点.ABCD是扇形的内接矩形,记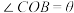 ,矩形
,矩形 的面积为
的面积为 .
.
(1)当 时,求矩形
时,求矩形 的面积
的面积 的值.
的值.
(2)求 关于角
关于角 的解析式,并求
的解析式,并求 的最大值.
的最大值.
 的扇形,C是扇形弧上的动点.ABCD是扇形的内接矩形,记
的扇形,C是扇形弧上的动点.ABCD是扇形的内接矩形,记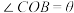 ,矩形
,矩形 的面积为
的面积为 .
.
(1)当
 时,求矩形
时,求矩形 的面积
的面积 的值.
的值.(2)求
 关于角
关于角 的解析式,并求
的解析式,并求 的最大值.
的最大值.
您最近一年使用:0次
名校
2 . 设常数a使方程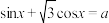 在闭区间
在闭区间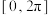 上恰有三个不同的解
上恰有三个不同的解 ,则实数a的取值集合为
,则实数a的取值集合为________ .
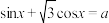 在闭区间
在闭区间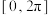 上恰有三个不同的解
上恰有三个不同的解 ,则实数a的取值集合为
,则实数a的取值集合为
您最近一年使用:0次
2023-02-26更新
|
697次组卷
|
3卷引用:上海市华东师范大学第二附属中学2022-2023学年高一下学期3月月考数学试题
(已下线)上海市华东师范大学第二附属中学2022-2023学年高一下学期3月月考数学试题湖北省黄冈市黄梅国际育才高级中学2022-2023学年高一下学期2月月考数学试题广东省汕头市潮阳启声学校2022-2023学年高一下学期3月月考数学试题
名校
解题方法
3 . 已知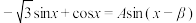 ,其中
,其中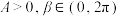 ,则
,则 ( )
( )
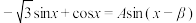 ,其中
,其中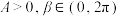 ,则
,则 ( )
( )A. | B. | C.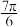 | D. |
您最近一年使用:0次
名校
解题方法
4 . 某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角 和以
和以 为直径的半圆拼接而成,点
为直径的半圆拼接而成,点 为半圆上一点(异于
为半圆上一点(异于 ,
, ),点
),点 在线段
在线段 上,且满足
上,且满足 .已知
.已知 ,
, ,设
,设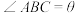 .
. ,且
,且 达到最大.当
达到最大.当 为何值时,工艺礼品达到最佳观赏效果?
为何值时,工艺礼品达到最佳观赏效果?
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足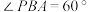 ,且
,且 达到最大.当
达到最大.当 为何值时,工艺礼品达到最佳稳定性?并求此时
为何值时,工艺礼品达到最佳稳定性?并求此时 的值.
的值.
 和以
和以 为直径的半圆拼接而成,点
为直径的半圆拼接而成,点 为半圆上一点(异于
为半圆上一点(异于 ,
, ),点
),点 在线段
在线段 上,且满足
上,且满足 .已知
.已知 ,
, ,设
,设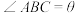 .
.
 ,且
,且 达到最大.当
达到最大.当 为何值时,工艺礼品达到最佳观赏效果?
为何值时,工艺礼品达到最佳观赏效果?(2)为了工艺礼品达到最佳稳定性便于收藏,需满足
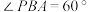 ,且
,且 达到最大.当
达到最大.当 为何值时,工艺礼品达到最佳稳定性?并求此时
为何值时,工艺礼品达到最佳稳定性?并求此时 的值.
的值.
您最近一年使用:0次
2024-03-15更新
|
655次组卷
|
5卷引用:上海市七宝中学2023-2024学年高一下学期期中考试数学试卷
名校
5 . 已知函数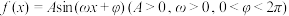 的部分图像如图所示.
的部分图像如图所示.
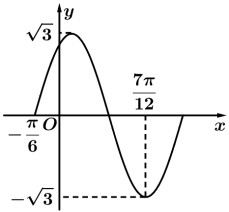
(1)求函数 的解析式;
的解析式;
(2)若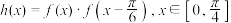 ,求
,求 的取值范围.
的取值范围.
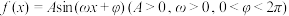 的部分图像如图所示.
的部分图像如图所示.
(1)求函数
 的解析式;
的解析式;(2)若
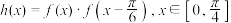 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2021-09-05更新
|
2272次组卷
|
10卷引用:上海市复旦大学附属中学2020-2021学年高一下学期期中数学试题
上海市复旦大学附属中学2020-2021学年高一下学期期中数学试题上海市第二中学2023届高三上学期期中数学试题河北省保定市唐县第一中学2022届高三上学期第二次考试数学试题(已下线)专题01 三角函数的图象与性质-【解题思路培养】2022年高考数学一轮复习解答题拿分秘籍(全国通用版)河南省三门峡市2021-2022学年高三上学期阶段性检测文科数学试题江西省贵溪市实验中学高中部2022届高三上学期三校生第三次月考数学试题四川省成都市蒲江县蒲江中学2021-2022学年高一下学期3月月考数学试题辽宁省沈阳市五校协作体2021-2022学年高一下学期期末数学试题(已下线)模块四 专题1 期末重组综合练(辽宁)(人教B)(已下线)期末专题02 三角函数5.4-5.7大题综合-【备战期末必刷真题】
2024·全国·模拟预测
6 . 已知函数 ,若
,若 的图象在
的图象在 上有且仅有两条对称轴,则
上有且仅有两条对称轴,则 的取值范围是
的取值范围是______ .
 ,若
,若 的图象在
的图象在 上有且仅有两条对称轴,则
上有且仅有两条对称轴,则 的取值范围是
的取值范围是
您最近一年使用:0次
2024-04-23更新
|
586次组卷
|
5卷引用:期末测试卷02-《期末真题分类汇编》(上海专用)
(已下线)期末测试卷02-《期末真题分类汇编》(上海专用)(已下线)2024年普通高等学校招生全国统一考试·押题卷数学(八)江苏省?邮市第?中学2023-2024学年高一下学期4月阶段测试数学试卷(已下线)4.3 二倍角的三角函数公式-同步精品课堂(北师大版2019必修第二册)江苏省南通市启东中学2023-2024学年高一下学期5月考试数学试题
名校
7 . 设函数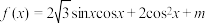 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当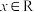 时,
时, 的最小值为2,求函数
的最小值为2,求函数 的最大值及对应的
的最大值及对应的 的值.
的值.
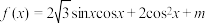 .
.(1)求函数
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(2)当
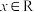 时,
时, 的最小值为2,求函数
的最小值为2,求函数 的最大值及对应的
的最大值及对应的 的值.
的值.
您最近一年使用:0次
2023-11-21更新
|
690次组卷
|
2卷引用:上海市松江区第四中学2023-2024学年高三上学期期中学情诊断数学试题
8 . 求下列各式的值:
(1) ;
;
(2)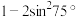 ;
;
(3)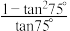 ;
;
(4)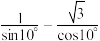 .
.
(1)
 ;
;(2)
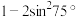 ;
;(3)
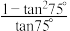 ;
;(4)
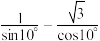 .
.
您最近一年使用:0次
名校
9 . 已知函数 ,任取
,任取 ,记函数
,记函数 在
在 上的最大值为
上的最大值为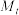 ,最小值为
,最小值为 ,设
,设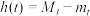 ,则函数
,则函数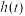 的值域为( )
的值域为( )
 ,任取
,任取 ,记函数
,记函数 在
在 上的最大值为
上的最大值为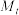 ,最小值为
,最小值为 ,设
,设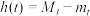 ,则函数
,则函数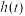 的值域为( )
的值域为( )A.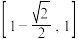 | B.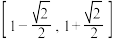 |
C.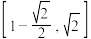 | D.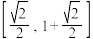 |
您最近一年使用:0次
2022-11-24更新
|
1374次组卷
|
5卷引用:上海市华东师范大学第二附属中学2024届高三上学期期中数学试题
(已下线)上海市华东师范大学第二附属中学2024届高三上学期期中数学试题四川省泸州市2022-2023学年高三上学期第一次教学质量诊断性考试数学(理)试题第10章《三角恒等变换》单元达标高分突破必刷卷(基础版)江西省全南中学2022-2023学年高一下学期期中数学试题(已下线)三角恒等变换
名校
10 . 已知函数 ,
, .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)求 在区间
在区间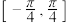 上的最大值和最小值.
上的最大值和最小值.
 ,
, .
.(1)求
 的单调递增区间;
的单调递增区间;(2)求
 在区间
在区间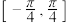 上的最大值和最小值.
上的最大值和最小值.
您最近一年使用:0次
2022-12-15更新
|
1398次组卷
|
3卷引用:上海市青浦区2023届高三一模数学试题



