名校
解题方法
1 . 数列 满足
满足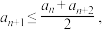 则称数列
则称数列 为下凸数列.
为下凸数列.
(1)证明:任意一个正项等比数列均为下凸数列;
(2)设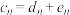 ,其中
,其中 ,
,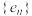 分别是公比为
分别是公比为 ,
,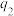 的两个正项等比数列,且
的两个正项等比数列,且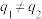 ,证明:
,证明: 是下凸数列且不是等比数列;
是下凸数列且不是等比数列;
(3)若正项下凸数列的前 项和为
项和为 ,且
,且 ,求证:
,求证: .
.
 满足
满足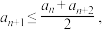 则称数列
则称数列 为下凸数列.
为下凸数列.(1)证明:任意一个正项等比数列均为下凸数列;
(2)设
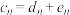 ,其中
,其中 ,
,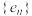 分别是公比为
分别是公比为 ,
,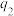 的两个正项等比数列,且
的两个正项等比数列,且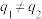 ,证明:
,证明: 是下凸数列且不是等比数列;
是下凸数列且不是等比数列;(3)若正项下凸数列的前
 项和为
项和为 ,且
,且 ,求证:
,求证: .
.
您最近一年使用:0次
7日内更新
|
1001次组卷
|
3卷引用:2024届广东省三模数学试题
2 . 已知 为坐标原点,
为坐标原点,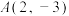 ,
,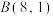 .
.
(1)判断 的形状,并给予证明;
的形状,并给予证明;
(2)若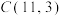 ,求证:
,求证: 、
、 、
、 三点共线;
三点共线;
(3)若 是线段
是线段 上靠近点
上靠近点 的四等分点,求
的四等分点,求 的坐标.
的坐标.
 为坐标原点,
为坐标原点,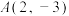 ,
,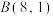 .
.(1)判断
 的形状,并给予证明;
的形状,并给予证明;(2)若
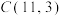 ,求证:
,求证: 、
、 、
、 三点共线;
三点共线;(3)若
 是线段
是线段 上靠近点
上靠近点 的四等分点,求
的四等分点,求 的坐标.
的坐标.
您最近一年使用:0次
解题方法
3 . 在数学中,不给出具体解析式,只给出函数满足的特殊条件或特征的函数称为“抽象函数”.我们需要研究抽象函数的定义域、单调性、奇偶性等性质.对于抽象函数 ,当
,当 时,
时, ,且满足:
,且满足: ,均有
,均有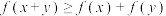
(1)证明: 在
在 上单调递增;
上单调递增;
(2)若函数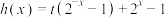 满足上述函数的特征,求实数
满足上述函数的特征,求实数 的取值范围;
的取值范围;
(3)若 ,求证:对任意
,求证:对任意 ,都有
,都有 .
.
 ,当
,当 时,
时, ,且满足:
,且满足: ,均有
,均有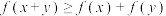
(1)证明:
 在
在 上单调递增;
上单调递增;(2)若函数
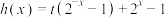 满足上述函数的特征,求实数
满足上述函数的特征,求实数 的取值范围;
的取值范围;(3)若
 ,求证:对任意
,求证:对任意 ,都有
,都有 .
.
您最近一年使用:0次
名校
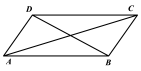
4 . (1)证明“直线与平面垂直的判定定理”:如果一条直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直.
已知:如图,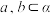 ,
,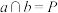 ,
,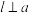 ,
, .求证:
.求证: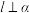 ;
;

(2)证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
如图,四边形 是平行四边形.求证:
是平行四边形.求证: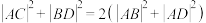 .
.
已知:如图,
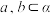 ,
,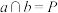 ,
,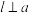 ,
, .求证:
.求证: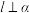 ;
;
(2)证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
如图,四边形
 是平行四边形.求证:
是平行四边形.求证: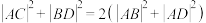 .
.
您最近一年使用:0次
名校
5 . 如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点P作弦 ,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.
,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.
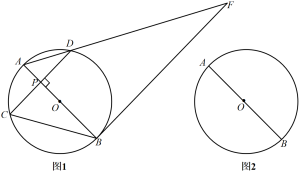
(1)若CD= ,BP=4,求⊙O的半径;
,BP=4,求⊙O的半径;
(2)求证:直线BF是⊙O的切线;
(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.
 ,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.
,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.
(1)若CD=
 ,BP=4,求⊙O的半径;
,BP=4,求⊙O的半径;(2)求证:直线BF是⊙O的切线;
(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.
您最近一年使用:0次
解题方法
6 . (1)求函数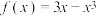 的单调区间.
的单调区间.
(2)用向量方法证明:已知直线l,a和平面 ,
,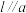 ,
, ,
, ,求证:
,求证: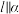 .
.
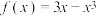 的单调区间.
的单调区间.(2)用向量方法证明:已知直线l,a和平面
 ,
,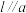 ,
, ,
, ,求证:
,求证: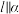 .
.
您最近一年使用:0次
解题方法
7 . 拉格朗日中值定理是微分学的基本定理之一,其内容为:如果函数 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且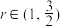 .
.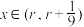 时,
时,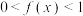 ;
;
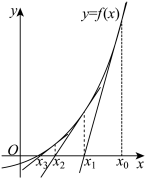
(2)从图形上看,函数 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得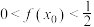 ,然后在点
,然后在点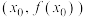 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列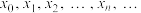 .
.
①当 时,证明:
时,证明: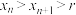 ;
;
②根据①的结论,运用数学归纳法可以证得: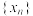 为递减数列,且
为递减数列,且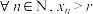 .请以此为前提条件,证明:
.请以此为前提条件,证明: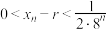 .
.
 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且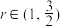 .
.
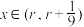 时,
时,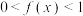 ;
;(2)从图形上看,函数
 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得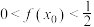 ,然后在点
,然后在点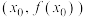 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列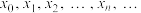 .
.①当
 时,证明:
时,证明: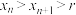 ;
;②根据①的结论,运用数学归纳法可以证得:
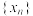 为递减数列,且
为递减数列,且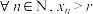 .请以此为前提条件,证明:
.请以此为前提条件,证明: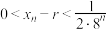 .
.
您最近一年使用:0次
8 . 若函数 的图象上的两个不同点处的切线互相重合,则称该切线为函数
的图象上的两个不同点处的切线互相重合,则称该切线为函数 的图象的“自公切线”,称这两点为函数
的图象的“自公切线”,称这两点为函数 的图象的一对“同切点”.
的图象的一对“同切点”.
(1)分别判断函数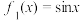 与
与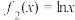 的图象是否存在“自公切线”,并说明理由;
的图象是否存在“自公切线”,并说明理由;
(2)若 ,求证:函数
,求证:函数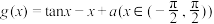 有唯一零点且该函数的图象不存在“自公切线”;
有唯一零点且该函数的图象不存在“自公切线”;
(3)设 ,
,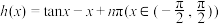 的零点为
的零点为 ,
, ,求证:“存在
,求证:“存在 ,使得点
,使得点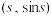 与
与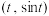 是函数
是函数 的图象的一对‘同切点’”的充要条件是“
的图象的一对‘同切点’”的充要条件是“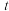 是数列
是数列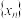 中的项”.
中的项”.
 的图象上的两个不同点处的切线互相重合,则称该切线为函数
的图象上的两个不同点处的切线互相重合,则称该切线为函数 的图象的“自公切线”,称这两点为函数
的图象的“自公切线”,称这两点为函数 的图象的一对“同切点”.
的图象的一对“同切点”.(1)分别判断函数
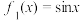 与
与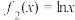 的图象是否存在“自公切线”,并说明理由;
的图象是否存在“自公切线”,并说明理由;(2)若
 ,求证:函数
,求证:函数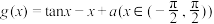 有唯一零点且该函数的图象不存在“自公切线”;
有唯一零点且该函数的图象不存在“自公切线”;(3)设
 ,
,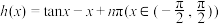 的零点为
的零点为 ,
, ,求证:“存在
,求证:“存在 ,使得点
,使得点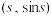 与
与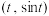 是函数
是函数 的图象的一对‘同切点’”的充要条件是“
的图象的一对‘同切点’”的充要条件是“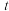 是数列
是数列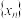 中的项”.
中的项”.
您最近一年使用:0次
9 . 定义两个 维向量
维向量 ,
, 的数量积
的数量积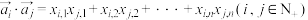 ,
,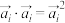 ,记
,记 为
为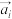 的第k个分量(
的第k个分量( 且
且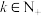 ).如三维向量
).如三维向量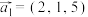 ,其中
,其中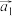 的第2分量
的第2分量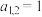 .若由
.若由 维向量组成的集合A满足以下三个条件:①集合中含有n个n维向量作为元素;②集合中每个元素的所有分量取0或1;③集合中任意两个元素
维向量组成的集合A满足以下三个条件:①集合中含有n个n维向量作为元素;②集合中每个元素的所有分量取0或1;③集合中任意两个元素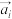 ,
,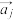 ,满足
,满足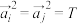 (T为常数)且
(T为常数)且 .则称A为T的完美n维向量集.
.则称A为T的完美n维向量集.
(1)求2的完美3维向量集;
(2)判断是否存在完美4维向量集,并说明理由;
(3)若存在A为T的完美n维向量集,求证:A的所有元素的第k分量和 .
.
 维向量
维向量 ,
, 的数量积
的数量积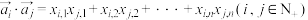 ,
,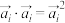 ,记
,记 为
为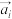 的第k个分量(
的第k个分量( 且
且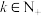 ).如三维向量
).如三维向量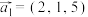 ,其中
,其中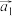 的第2分量
的第2分量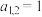 .若由
.若由 维向量组成的集合A满足以下三个条件:①集合中含有n个n维向量作为元素;②集合中每个元素的所有分量取0或1;③集合中任意两个元素
维向量组成的集合A满足以下三个条件:①集合中含有n个n维向量作为元素;②集合中每个元素的所有分量取0或1;③集合中任意两个元素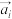 ,
,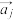 ,满足
,满足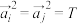 (T为常数)且
(T为常数)且 .则称A为T的完美n维向量集.
.则称A为T的完美n维向量集.(1)求2的完美3维向量集;
(2)判断是否存在完美4维向量集,并说明理由;
(3)若存在A为T的完美n维向量集,求证:A的所有元素的第k分量和
 .
.
您最近一年使用:0次
2024-04-23更新
|
639次组卷
|
2卷引用:广东省汕头市潮阳区河溪中学2023-2024学年高三下学期第二学月质检数学试题
解题方法
10 . 在组合恒等式的证明中,构造一个具体的计数模型从而证明组合恒等式的方法叫做组合分析法,该方法体现了数学的简洁美,我们将通过如下的例子感受其妙处所在.
(1)对于 元一次方程
元一次方程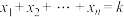 ,试求其正整数解的个数;
,试求其正整数解的个数;
(2)对于 元一次方程组
元一次方程组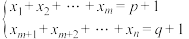 ,试求其非负整数解的个数;
,试求其非负整数解的个数;
(3)证明: (可不使用组合分析法证明).
(可不使用组合分析法证明).
注: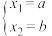 与
与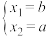 可视为二元一次方程的两组不同解.
可视为二元一次方程的两组不同解.
(1)对于
 元一次方程
元一次方程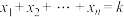 ,试求其正整数解的个数;
,试求其正整数解的个数;(2)对于
 元一次方程组
元一次方程组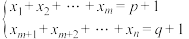 ,试求其非负整数解的个数;
,试求其非负整数解的个数;(3)证明:
 (可不使用组合分析法证明).
(可不使用组合分析法证明).注:
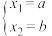 与
与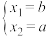 可视为二元一次方程的两组不同解.
可视为二元一次方程的两组不同解.
您最近一年使用:0次
2024-03-08更新
|
1055次组卷
|
3卷引用:广东省五粤名校联盟2024届高三第一次联考数学试题



