名校
1 . 根据多元微分求条件极值理论,要求二元函数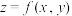 在约束条件
在约束条件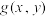 的可能极值点,首先构造出一个拉格朗日辅助函数
的可能极值点,首先构造出一个拉格朗日辅助函数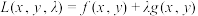 ,其中
,其中 为拉格朗日系数.分别对
为拉格朗日系数.分别对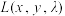 中的
中的 部分求导,并使之为0,得到三个方程组,如下:
部分求导,并使之为0,得到三个方程组,如下:
 ,解此方程组,得出解
,解此方程组,得出解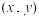 ,就是二元函数
,就是二元函数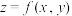 在约束条件
在约束条件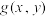 的可能极值点.
的可能极值点. 的值代入到
的值代入到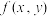 中即为极值.
中即为极值.
补充说明:【例】求函数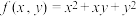 关于变量
关于变量 的导数.即:将变量
的导数.即:将变量 当做常数,即:
当做常数,即: ,下标加上
,下标加上 ,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的
,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的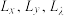 表示分别对
表示分别对 进行求导.
进行求导.
(1)求函数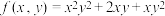 关于变量
关于变量 的导数并求当
的导数并求当 处的导数值.
处的导数值.
(2)利用拉格朗日乘数法求:设实数 满足
满足 ,求
,求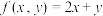 的最大值.
的最大值.
(3)①若 为实数,且
为实数,且 ,证明:
,证明: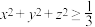 .
.
②设 ,求
,求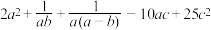 的最小值.
的最小值.
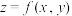 在约束条件
在约束条件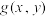 的可能极值点,首先构造出一个拉格朗日辅助函数
的可能极值点,首先构造出一个拉格朗日辅助函数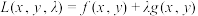 ,其中
,其中 为拉格朗日系数.分别对
为拉格朗日系数.分别对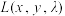 中的
中的 部分求导,并使之为0,得到三个方程组,如下:
部分求导,并使之为0,得到三个方程组,如下: ,解此方程组,得出解
,解此方程组,得出解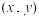 ,就是二元函数
,就是二元函数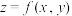 在约束条件
在约束条件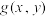 的可能极值点.
的可能极值点. 的值代入到
的值代入到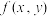 中即为极值.
中即为极值.补充说明:【例】求函数
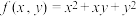 关于变量
关于变量 的导数.即:将变量
的导数.即:将变量 当做常数,即:
当做常数,即: ,下标加上
,下标加上 ,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的
,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的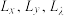 表示分别对
表示分别对 进行求导.
进行求导.(1)求函数
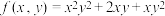 关于变量
关于变量 的导数并求当
的导数并求当 处的导数值.
处的导数值.(2)利用拉格朗日乘数法求:设实数
 满足
满足 ,求
,求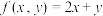 的最大值.
的最大值.(3)①若
 为实数,且
为实数,且 ,证明:
,证明: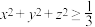 .
.②设
 ,求
,求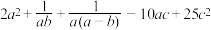 的最小值.
的最小值.
您最近一年使用:0次
名校
2 . 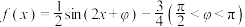 ,且
,且 .
.
(1)方程 在
在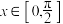 有且仅有一个解,求
有且仅有一个解,求 的取值范围.
的取值范围.
(2)设 ,对
,对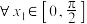 ,总
,总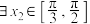 ,使
,使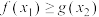 成立,求
成立,求 的范围.
的范围.
(3)若 与
与 的图象关于
的图象关于 对称,求不等式
对称,求不等式 的解集.
的解集.
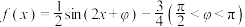 ,且
,且 .
.(1)方程
 在
在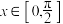 有且仅有一个解,求
有且仅有一个解,求 的取值范围.
的取值范围.(2)设
 ,对
,对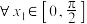 ,总
,总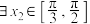 ,使
,使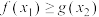 成立,求
成立,求 的范围.
的范围.(3)若
 与
与 的图象关于
的图象关于 对称,求不等式
对称,求不等式 的解集.
的解集.
您最近一年使用:0次
2023-05-21更新
|
1189次组卷
|
6卷引用:专题5.9 三角函数全章八类必考压轴题-举一反三系列
(已下线)专题5.9 三角函数全章八类必考压轴题-举一反三系列(已下线)专题5.4 三角函数的图象与性质-举一反三系列(已下线)第七章 三角函数(压轴题专练)-单元速记·巧练(沪教版2020必修第二册)辽宁省沈阳市第十一中学2022-2023学年高一下学期4月月考数学试题江西省吉安市双校联盟2022-2023学年高一下学期期中考试数学试题(已下线)模块四 专题2 重组综合练(江西)(北师版高一期中)
2022·上海·模拟预测
3 . 已知函数 ,甲变化:
,甲变化: ;乙变化:
;乙变化: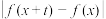 ,
, .
.
(1)若 ,
, ,
, 经甲变化得到
经甲变化得到 ,求方程
,求方程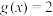 的解;
的解;
(2)若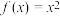 ,
, 经乙变化得到
经乙变化得到 ,求不等式
,求不等式 的解集;
的解集;
(3)若 在
在 上单调递增,将
上单调递增,将 先进行甲变化得到
先进行甲变化得到 ,再将
,再将 进行乙变化得到
进行乙变化得到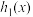 ;将
;将 先进行乙变化得到
先进行乙变化得到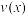 ,再将
,再将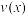 进行甲变化得到
进行甲变化得到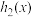 ,若对任意
,若对任意 ,总存在
,总存在 成立,求证:
成立,求证: 在R上单调递增.
在R上单调递增.
 ,甲变化:
,甲变化: ;乙变化:
;乙变化: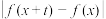 ,
, .
.(1)若
 ,
, ,
, 经甲变化得到
经甲变化得到 ,求方程
,求方程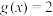 的解;
的解;(2)若
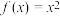 ,
, 经乙变化得到
经乙变化得到 ,求不等式
,求不等式 的解集;
的解集;(3)若
 在
在 上单调递增,将
上单调递增,将 先进行甲变化得到
先进行甲变化得到 ,再将
,再将 进行乙变化得到
进行乙变化得到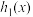 ;将
;将 先进行乙变化得到
先进行乙变化得到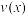 ,再将
,再将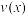 进行甲变化得到
进行甲变化得到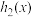 ,若对任意
,若对任意 ,总存在
,总存在 成立,求证:
成立,求证: 在R上单调递增.
在R上单调递增.
您最近一年使用:0次
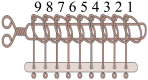
4 . 九连环是中国一种古老的智力游戏,其结构如图,玩九连环就是要把这九个环全部从框架上解下或套上.研究发现,要解下第 个环,则必须先解下前面第
个环,则必须先解下前面第 个环.用
个环.用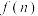 表示解下
表示解下 个环所需最少移动次数,用
个环所需最少移动次数,用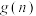 表示前
表示前 个环都已经解下后,再解下第
个环都已经解下后,再解下第 个环所需次数,显然,
个环所需次数,显然,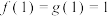 ,
,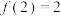 ,且
,且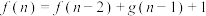 .若要将第
.若要将第 个环解下,则必须先将第
个环解下,则必须先将第 个环套回框架,这个过程需要移动
个环套回框架,这个过程需要移动 次,这时再移动1次,就可以解下第
次,这时再移动1次,就可以解下第 个环;然后再将第
个环;然后再将第 个环解下,又需要移动
个环解下,又需要移动 次.由此可得,
次.由此可得,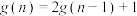 .据此计算
.据此计算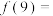
______ .
 个环,则必须先解下前面第
个环,则必须先解下前面第 个环.用
个环.用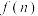 表示解下
表示解下 个环所需最少移动次数,用
个环所需最少移动次数,用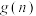 表示前
表示前 个环都已经解下后,再解下第
个环都已经解下后,再解下第 个环所需次数,显然,
个环所需次数,显然,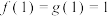 ,
,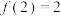 ,且
,且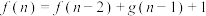 .若要将第
.若要将第 个环解下,则必须先将第
个环解下,则必须先将第 个环套回框架,这个过程需要移动
个环套回框架,这个过程需要移动 次,这时再移动1次,就可以解下第
次,这时再移动1次,就可以解下第 个环;然后再将第
个环;然后再将第 个环解下,又需要移动
个环解下,又需要移动 次.由此可得,
次.由此可得,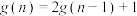 .据此计算
.据此计算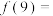
您最近一年使用:0次
2022·上海浦东新·模拟预测
名校
解题方法
5 . 已知定义域为 的函数
的函数 .当
.当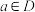 时,若
时,若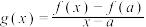 (
( ,
,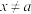 )是增函数,则称
)是增函数,则称 是一个“
是一个“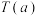 函数”.
函数”.
(1)判断函数 (
( )是否为
)是否为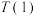 函数,并说明理由;
函数,并说明理由;
(2)若定义域为 的
的 函数
函数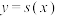 满足
满足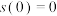 ,解关于
,解关于 的不等式
的不等式 ;
;
(3)设 是满足下列条件的定义域为
是满足下列条件的定义域为 的函数
的函数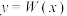 组成的集合:①对任意
组成的集合:①对任意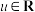 ,
,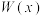 都是
都是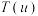 函数;②
函数;②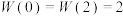 ,
, . 若
. 若 对一切
对一切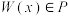 和所有
和所有 成立,求实数
成立,求实数 的最大值.
的最大值.
 的函数
的函数 .当
.当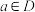 时,若
时,若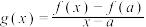 (
( ,
,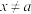 )是增函数,则称
)是增函数,则称 是一个“
是一个“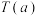 函数”.
函数”.(1)判断函数
 (
( )是否为
)是否为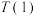 函数,并说明理由;
函数,并说明理由;(2)若定义域为
 的
的 函数
函数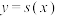 满足
满足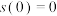 ,解关于
,解关于 的不等式
的不等式 ;
;(3)设
 是满足下列条件的定义域为
是满足下列条件的定义域为 的函数
的函数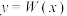 组成的集合:①对任意
组成的集合:①对任意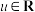 ,
,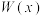 都是
都是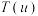 函数;②
函数;②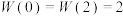 ,
, . 若
. 若 对一切
对一切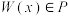 和所有
和所有 成立,求实数
成立,求实数 的最大值.
的最大值.
您最近一年使用:0次
2022-07-05更新
|
1738次组卷
|
8卷引用:考向10函数与导数(重点)-2
(已下线)考向10函数与导数(重点)-2(已下线)第三章 函数的概念与性质单元测试基础卷-人教A版(2019)必修第一册(已下线)上海市华东师范大学第二附属中学2022届高三考前模拟数学试题上海市行知中学2023届高三上学期10月月考数学试题上海市曹杨第二中学2023届高三上学期12月月考数学试题广东省广州市华附2023-2024学年高一上学期期中数学试题2024届高三新高考改革数学适应性练习(九省联考题型)广东省茂名市电白区第一中学2023-2024学年高一下学期4月月考数学试题
6 . 同余定理是数论中的重要内容.同余的定义为:设a,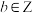 ,
, 且
且 .若
.若 则称a与b关于模m同余,记作
则称a与b关于模m同余,记作 (modm)(“|”为整除符号).
(modm)(“|”为整除符号).
(1)解同余方程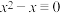 (mod3);
(mod3);
(2)设(1)中方程的所有正根构成数列 ,其中
,其中 .
.
①若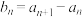 (
( ),数列
),数列 的前n项和为
的前n项和为 ,求
,求 ;
;
②若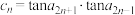 (
( ),求数列
),求数列 的前n项和
的前n项和 .
.
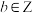 ,
, 且
且 .若
.若 则称a与b关于模m同余,记作
则称a与b关于模m同余,记作 (modm)(“|”为整除符号).
(modm)(“|”为整除符号).(1)解同余方程
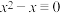 (mod3);
(mod3);(2)设(1)中方程的所有正根构成数列
 ,其中
,其中 .
.①若
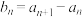 (
( ),数列
),数列 的前n项和为
的前n项和为 ,求
,求 ;
;②若
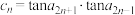 (
( ),求数列
),求数列 的前n项和
的前n项和 .
.
您最近一年使用:0次
2024-02-03更新
|
2803次组卷
|
9卷引用:压轴题函数与导数新定义题(九省联考第19题模式)练
(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)新题型01 新高考新结构二十一大考点汇总-3(已下线)黄金卷08(2024新题型)(已下线)题型18 4类数列综合安徽省合肥市第一中学2024届高三上学期期末质量检测数学试题湖北省武汉市华中师大第一附中2023-2024学年高二下学期数学独立作业(一)重庆市万州二中教育集团2023-2024学年高二下学期入学质量监测数学试题浙江省部分学校联考2024届高三高考适应性测试数学试题广东省揭阳市普宁市华美实验学校2023-2024学年高二下学期第一次阶段考试数学试题
2024高三上·全国·专题练习
7 . 已知函数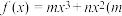 、
、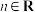 ,
,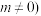 的图象在
的图象在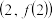 处的切线与
处的切线与 轴平行.
轴平行.
(1)求 ,
, 的关系式并求
的关系式并求 的单调减区间;
的单调减区间;
(2)证明:对任意实数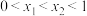 ,关于
,关于 的方程:
的方程: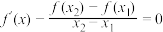 在
在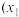 ,
,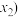 恒有实数解;
恒有实数解;
(3)结合(2)的结论,其实我们有拉格朗日中值定理:若函数 是在闭区间
是在闭区间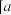 ,
,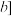 上连续不断的函数,且在区间
上连续不断的函数,且在区间 内导数都存在,则在
内导数都存在,则在 内至少存在一点
内至少存在一点 ,使得
,使得 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
当 时,
时,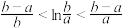 (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性).
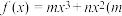 、
、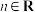 ,
,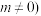 的图象在
的图象在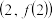 处的切线与
处的切线与 轴平行.
轴平行.(1)求
 ,
, 的关系式并求
的关系式并求 的单调减区间;
的单调减区间;(2)证明:对任意实数
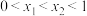 ,关于
,关于 的方程:
的方程: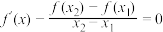 在
在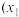 ,
,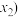 恒有实数解;
恒有实数解;(3)结合(2)的结论,其实我们有拉格朗日中值定理:若函数
 是在闭区间
是在闭区间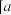 ,
,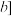 上连续不断的函数,且在区间
上连续不断的函数,且在区间 内导数都存在,则在
内导数都存在,则在 内至少存在一点
内至少存在一点 ,使得
,使得 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:当
 时,
时,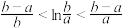 (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性).
您最近一年使用:0次
名校
解题方法
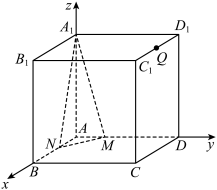
8 . 设常数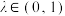 .在棱长为1的正方体
.在棱长为1的正方体 中,点
中,点 满足
满足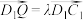 ,点
,点 分别为棱
分别为棱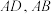 上的动点(均不与顶点重合),且满足
上的动点(均不与顶点重合),且满足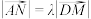 ,记
,记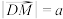 .以
.以 为原点,分别以
为原点,分别以 的方向为
的方向为 轴的正方向,建立如图空间直角坐标系
轴的正方向,建立如图空间直角坐标系
(1)用 和
和 表示点
表示点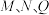 的坐标;
的坐标;
(2)设 ,若
,若 ,求常数
,求常数 的值;
的值;
(3)记 到平面
到平面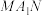 的距离为
的距离为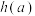 .求证:若关于
.求证:若关于 的方程
的方程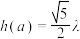 在
在 上恰有两个不同的解,则这两个解中至少有一个大于
上恰有两个不同的解,则这两个解中至少有一个大于 .
.
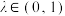 .在棱长为1的正方体
.在棱长为1的正方体 中,点
中,点 满足
满足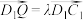 ,点
,点 分别为棱
分别为棱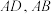 上的动点(均不与顶点重合),且满足
上的动点(均不与顶点重合),且满足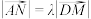 ,记
,记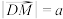 .以
.以 为原点,分别以
为原点,分别以 的方向为
的方向为 轴的正方向,建立如图空间直角坐标系
轴的正方向,建立如图空间直角坐标系
(1)用
 和
和 表示点
表示点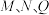 的坐标;
的坐标;(2)设
 ,若
,若 ,求常数
,求常数 的值;
的值;(3)记
 到平面
到平面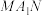 的距离为
的距离为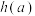 .求证:若关于
.求证:若关于 的方程
的方程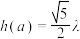 在
在 上恰有两个不同的解,则这两个解中至少有一个大于
上恰有两个不同的解,则这两个解中至少有一个大于 .
.
您最近一年使用:0次
名校
9 . 在面积为 的
的 中,内角
中,内角 所对的边分别为
所对的边分别为 ,且
,且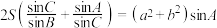 .
.
(1)若 为锐角三角形,
为锐角三角形, 是关于
是关于 的方程
的方程 的解,求
的解,求 的取值范围;
的取值范围;
(2)若 且
且 的外接圆的直径为8,
的外接圆的直径为8, 分别在线段
分别在线段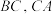 上运动(包括端点),
上运动(包括端点), 为边
为边 的中点,且
的中点,且 ,
,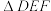 的面积为
的面积为 .令
.令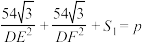 ,求
,求 的最小值.
的最小值.
 的
的 中,内角
中,内角 所对的边分别为
所对的边分别为 ,且
,且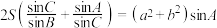 .
.(1)若
 为锐角三角形,
为锐角三角形, 是关于
是关于 的方程
的方程 的解,求
的解,求 的取值范围;
的取值范围;(2)若
 且
且 的外接圆的直径为8,
的外接圆的直径为8, 分别在线段
分别在线段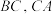 上运动(包括端点),
上运动(包括端点), 为边
为边 的中点,且
的中点,且 ,
,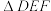 的面积为
的面积为 .令
.令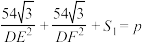 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
10 . 在概率较难计算但数据量相当大、误差允许的情况下,可以使用UnionBound(布尔不等式)进行估计概率.已知UnionBound不等式为:记随机事件 ,则
,则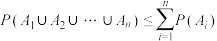 .其误差允许下可将左右两边视为近似相等.据此解决以下问题:
.其误差允许下可将左右两边视为近似相等.据此解决以下问题:
(1)有 个不同的球,其中
个不同的球,其中 个有数字标号.每次等概率随机抽取
个有数字标号.每次等概率随机抽取 个球中的一个球.抽完后放回.记抽取
个球中的一个球.抽完后放回.记抽取 次球后
次球后 个有数字标号的球每个都至少抽了一次的概率为
个有数字标号的球每个都至少抽了一次的概率为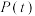 ,现在给定常数
,现在给定常数 ,则满足
,则满足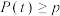 的
的 的最小值为多少?请用UnionBound估计其近似的最小值,结果不用取整.这里
的最小值为多少?请用UnionBound估计其近似的最小值,结果不用取整.这里 相当大且远大于
相当大且远大于 ;
;
(2)然而实际情况中,UnionBound精度往往不够,因此需要用容斥原理求出精确值.已知概率容斥原理:记随机事件 ,则
,则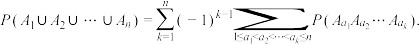 .试问在(1)的情况下,用容斥原理求出的精确的
.试问在(1)的情况下,用容斥原理求出的精确的 的最小值是多少(结果不用取整)?
的最小值是多少(结果不用取整)? 相当大且远大于
相当大且远大于 .
.
(1)(2)问参考数据:当 相当大时,取
相当大时,取 .
.
 ,则
,则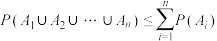 .其误差允许下可将左右两边视为近似相等.据此解决以下问题:
.其误差允许下可将左右两边视为近似相等.据此解决以下问题:(1)有
 个不同的球,其中
个不同的球,其中 个有数字标号.每次等概率随机抽取
个有数字标号.每次等概率随机抽取 个球中的一个球.抽完后放回.记抽取
个球中的一个球.抽完后放回.记抽取 次球后
次球后 个有数字标号的球每个都至少抽了一次的概率为
个有数字标号的球每个都至少抽了一次的概率为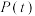 ,现在给定常数
,现在给定常数 ,则满足
,则满足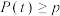 的
的 的最小值为多少?请用UnionBound估计其近似的最小值,结果不用取整.这里
的最小值为多少?请用UnionBound估计其近似的最小值,结果不用取整.这里 相当大且远大于
相当大且远大于 ;
;(2)然而实际情况中,UnionBound精度往往不够,因此需要用容斥原理求出精确值.已知概率容斥原理:记随机事件
 ,则
,则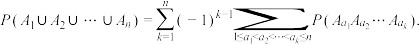 .试问在(1)的情况下,用容斥原理求出的精确的
.试问在(1)的情况下,用容斥原理求出的精确的 的最小值是多少(结果不用取整)?
的最小值是多少(结果不用取整)? 相当大且远大于
相当大且远大于 .
.(1)(2)问参考数据:当
 相当大时,取
相当大时,取 .
.
您最近一年使用:0次
2024-05-16更新
|
1285次组卷
|
3卷引用:压轴题08计数原理、二项式定理、概率统计压轴题6题型汇总



