1 . 帕德近似是法国数学家亨利·帕德发明的用有理多项式近似特定函数的方法.给定两个正整数 ,
, ,函数
,函数 在
在 处的
处的 阶帕德近似定义为:
阶帕德近似定义为: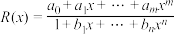 ,且满足:
,且满足: ,
, ,
,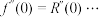 ,
,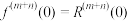 .已知
.已知 在
在 处的
处的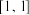 阶帕德近似为
阶帕德近似为 .注:
.注:
(1)求实数 ,
, 的值;
的值;
(2)求证: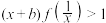 ;
;
(3)求不等式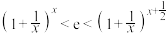 的解集,其中
的解集,其中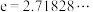 .
.
 ,
, ,函数
,函数 在
在 处的
处的 阶帕德近似定义为:
阶帕德近似定义为: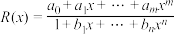 ,且满足:
,且满足: ,
, ,
,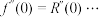 ,
,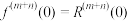 .已知
.已知 在
在 处的
处的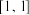 阶帕德近似为
阶帕德近似为 .注:
.注:
(1)求实数
 ,
, 的值;
的值;(2)求证:
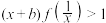 ;
;(3)求不等式
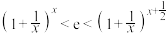 的解集,其中
的解集,其中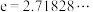 .
.
您最近一年使用:0次
2023-04-26更新
|
2460次组卷
|
17卷引用:山东省济南市2022-2023学年高二下学期期中数学试题
山东省济南市2022-2023学年高二下学期期中数学试题 重庆市巴蜀中学校2023届高三下学期4月月考数学试题吉林省白山市抚松县第一中学2022-2023学年高三第十一次校内模拟数学试题(已下线)第十章 导数与数学文化 微点2 导数与数学文化(二)(已下线)重难点突破02 函数的综合应用(九大题型)(已下线)第六套 九省联考全真模拟(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编(已下线)微考点8-1 新高考新题型19题新定义题型精选(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)(已下线)专题2 导数在研究函数单调性中的应用(B)重庆市璧山来凤中学校2023-2024学年高二下学期3月月考数学试题甘肃省白银市靖远县第四中学2023-2024学年高二下学期4月月考数学试题广东省中山市华辰实验中学2023-2024学年高二下学期第一次月考数学试题(已下线)模块四 期中重组篇(高二下山东)(已下线)模块3 第8套 复盘卷(已下线)模块一 专题2 《导数在研究函数单调性中的应用》 B提升卷(苏教版)(已下线)专题12 帕德逼近与不等式证明【练】
2 . “完全数”是一类特殊的自然数,它的所有正因数的和等于它自身的两倍.寻找“完全数”用到函数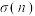 :
: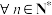 ,
,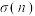 为n的所有正因数之和,如
为n的所有正因数之和,如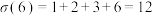 ,则
,则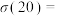
_______ ;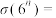
_______ .
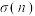 :
: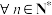 ,
,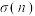 为n的所有正因数之和,如
为n的所有正因数之和,如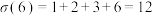 ,则
,则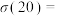
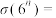
您最近一年使用:0次
2023-03-29更新
|
2465次组卷
|
10卷引用:江苏省八市(南通、泰州、扬州、徐州、淮安、连云港、宿迁、盐城)2023届高三二模数学试题
江苏省八市(南通、泰州、扬州、徐州、淮安、连云港、宿迁、盐城)2023届高三二模数学试题(已下线)江苏省八市2023届高三二模数学试题变式题11-16专题03函数的概念与基本初等函数江苏省八市2023届高三下学期第二次调研测试数学试题(已下线)阶段性检测2.2(中)(范围:集合至复数)(已下线)专题05 等比数列与数列综合求和-2023-2024学年高二数学期末复习重难培优与单元检测(人教A版2019)河南省周口市西华县第三高级中学2024届高三上学期期末统考数学试题湖南省湘潭市湘潭县第一中学2024届高三下学期2月月考数学试题安徽省安庆市第一中学2023-2024学年高二下学期第一次阶段性检测(期中)数学试题2024届安徽省阜阳市皖江名校联盟高三模拟预测数学试题
名校
3 . 在平面直角坐标系中,将函数 的图象绕坐标原点逆时针旋转
的图象绕坐标原点逆时针旋转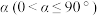 后,所得曲线仍然是某个函数的图象,则称
后,所得曲线仍然是某个函数的图象,则称 为“
为“ 旋转函数”.那么( )
旋转函数”.那么( )
 的图象绕坐标原点逆时针旋转
的图象绕坐标原点逆时针旋转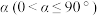 后,所得曲线仍然是某个函数的图象,则称
后,所得曲线仍然是某个函数的图象,则称 为“
为“ 旋转函数”.那么( )
旋转函数”.那么( )A.存在 旋转函数 旋转函数 |
B.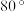 旋转函数一定是 旋转函数一定是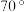 旋转函数 旋转函数 |
C.若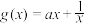 为 为 旋转函数,则 旋转函数,则 |
D.若 为 为 旋转函数,则 旋转函数,则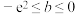 |
您最近一年使用:0次
2023-05-02更新
|
2446次组卷
|
10卷引用:湖北省星云联盟2023届高三下学期统一模拟考试Ⅱ数学试题
湖北省星云联盟2023届高三下学期统一模拟考试Ⅱ数学试题2023年普通高等学校招生星云线上统一模拟考试Ⅱ数学试题山东省淄博实验中学2023届高三第三次模拟考试数学试题江苏省苏州实验中学2022-2023学年高二下学期学情检测(二)数学试题浙江省名校协作体2024届高三下学期开学适应性考试数学试题(已下线)新题型01 新高考新结构二十一大考点汇总-2江苏省常州市前黄高级中学2024届高三下学期一模适应性考试数学试题江苏省苏州园三2023-2024学年高二下学期3月月考数学试题(已下线)专题8 函数新定义问题(过关集训)(压轴题大全)(已下线)压轴题01集合新定义、函数与导数13题型汇总-2
4 . 若函数 ,
, 的图象与直线
的图象与直线 分别交于A,B两点,与直线
分别交于A,B两点,与直线 分别交于C,D两点
分别交于C,D两点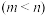 ,且直线
,且直线 ,
, 的斜率互为相反数,则称
的斜率互为相反数,则称 ,
, 为“
为“ 相关函数”.
相关函数”.
(1) ,
, 均为定义域上的单调递增函数,证明:不存在实数m,n,使得
均为定义域上的单调递增函数,证明:不存在实数m,n,使得 ,
, 为“
为“ 相关函数”;
相关函数”;
(2)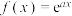 ,
, ,若存在实数
,若存在实数 ,使得
,使得 ,
, 为“
为“ 相关函数”,且
相关函数”,且 ,求实数a的取值范围.
,求实数a的取值范围.
 ,
, 的图象与直线
的图象与直线 分别交于A,B两点,与直线
分别交于A,B两点,与直线 分别交于C,D两点
分别交于C,D两点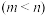 ,且直线
,且直线 ,
, 的斜率互为相反数,则称
的斜率互为相反数,则称 ,
, 为“
为“ 相关函数”.
相关函数”.(1)
 ,
, 均为定义域上的单调递增函数,证明:不存在实数m,n,使得
均为定义域上的单调递增函数,证明:不存在实数m,n,使得 ,
, 为“
为“ 相关函数”;
相关函数”;(2)
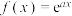 ,
, ,若存在实数
,若存在实数 ,使得
,使得 ,
, 为“
为“ 相关函数”,且
相关函数”,且 ,求实数a的取值范围.
,求实数a的取值范围.
您最近一年使用:0次
2023-02-11更新
|
2390次组卷
|
4卷引用:浙江省温州市2023届高三下学期返校统一测试数学试题
名校
5 . 已知函数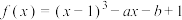 ,则下列结论正确的是( )
,则下列结论正确的是( )
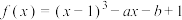 ,则下列结论正确的是( )
,则下列结论正确的是( )A.当 时,若 时,若 有三个零点,则b的取值范围为 有三个零点,则b的取值范围为 |
B.若 满足 满足 ,则 ,则 |
C.若过点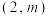 可作出曲线 可作出曲线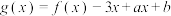 的三条切线,则 的三条切线,则 |
D.若 存在极值点 存在极值点 ,且 ,且 ,其中 ,其中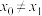 ,则 ,则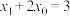 |
您最近一年使用:0次
2023-03-25更新
|
1917次组卷
|
10卷引用:山东省枣庄市2023届高三下学期第二次模拟考试数学试题
名校
6 . 已知函数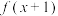 是偶函数,且
是偶函数,且 .当
.当 时,
时, ,则下列说法正确的是( )
,则下列说法正确的是( )
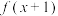 是偶函数,且
是偶函数,且 .当
.当 时,
时, ,则下列说法正确的是( )
,则下列说法正确的是( )A. 是奇函数 是奇函数 |
B. 在区间 在区间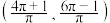 上有且只有一个零点 上有且只有一个零点 |
C. 在 在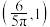 上单调递增 上单调递增 |
D. 区间 区间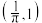 上有且只有一个极值点 上有且只有一个极值点 |
您最近一年使用:0次
2023-02-16更新
|
1883次组卷
|
7卷引用:安徽省合肥市2023届高三下学期第一次教学质量检测数学试题
安徽省合肥市2023届高三下学期第一次教学质量检测数学试题(已下线)专题04导数及其应用(选填题)(已下线)河北省石家庄市2023届高三质量检测(一)数学试题变式题11-16陕西省联盟学校2023届高三下学期第三次大联考理科数学试题(已下线)第九章 导数与三角函数的联袂 专题二 导数法求含三角函数的函数极值与最值 微点3 导数法求含三角函数的函数极值与最值综合训练重庆市第一中学校2023-2024学年高二上学期12月定时练习数学试题(已下线)专题23 导数及其应用小题
名校
7 . 如图所示,梯形 中,
中,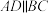 ,点
,点 为
为 的中点,
的中点, ,
, ,若向量
,若向量 在向量
在向量 上的投影向量的模为4,设
上的投影向量的模为4,设 、
、 分别为线段
分别为线段 、
、 上的动点,且
上的动点,且 ,
, ,则
,则 的取值范围是( )
的取值范围是( )
 中,
中, ,点
,点 为
为 的中点,
的中点, ,
, ,若向量
,若向量 在向量
在向量 上的投影向量的模为4,设
上的投影向量的模为4,设 、
、 分别为线段
分别为线段 、
、 上的动点,且
上的动点,且 ,
, ,则
,则 的取值范围是( )
的取值范围是( )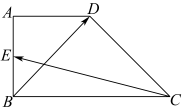
A.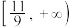 | B.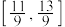 | C.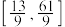 | D.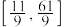 |
您最近一年使用:0次
2023-03-31更新
|
1809次组卷
|
4卷引用:天津市十二区重点学校2023届高三下学期毕业班联考(一)数学试题
天津市十二区重点学校2023届高三下学期毕业班联考(一)数学试题(已下线)高一数学下学期期中模拟试题01(平面向量、解三角形、复数、立体几何)黑龙江省哈尔滨市实验中学2022-2023学年高一下学期第一次月考数学试卷江西省景德镇市乐平中学2023-2024学年高一下学期5月月考数学试题
解题方法
8 . 设 是定义域为
是定义域为 的奇函数,且
的奇函数,且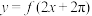 的图象关于直线
的图象关于直线 对称,若
对称,若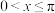 时,
时, ,则( )
,则( )
 是定义域为
是定义域为 的奇函数,且
的奇函数,且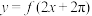 的图象关于直线
的图象关于直线 对称,若
对称,若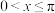 时,
时, ,则( )
,则( )A.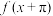 为偶函数 为偶函数 |
B. 在 在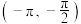 上单调递减 上单调递减 |
C. 在区间 在区间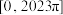 上有4046个零点 上有4046个零点 |
D.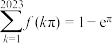 |
您最近一年使用:0次
2023-03-10更新
|
1720次组卷
|
4卷引用:河北省石家庄市2023届高三质量检测(一)数学试题
河北省石家庄市2023届高三质量检测(一)数学试题贵州省贵阳清镇北大培文学校2022-2023学年高二下学期3月月考数学试题重庆市缙云教育联盟2023届高三二模数学试题(已下线)河北省石家庄市2023届高三质量检测(一)数学试题变式题11-16
解题方法
9 . 已知定义在 上的单调递增的函数
上的单调递增的函数 满足:任意
满足:任意 ,有
,有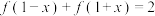 ,
, ,则( )
,则( )
 上的单调递增的函数
上的单调递增的函数 满足:任意
满足:任意 ,有
,有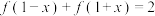 ,
, ,则( )
,则( )A.当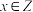 时, 时, |
B.任意 , , |
C.存在非零实数 ,使得任意 ,使得任意 , ,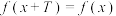 |
D.存在非零实数 ,使得任意 ,使得任意 , , |
您最近一年使用:0次
2022-04-19更新
|
3300次组卷
|
8卷引用:3.2.2 函数的性质(二)(精讲)-【一隅三反】2023年高考数学一轮复习(提升版)(新高考地区专用)
(已下线)3.2.2 函数的性质(二)(精讲)-【一隅三反】2023年高考数学一轮复习(提升版)(新高考地区专用)(已下线)考向06 函数的奇偶性与周期性、对称性(重点)(已下线)技巧01 单选题和多选题的答题技巧(精讲精练)-3江苏省泰州市兴化市2022届高三下学期4月模拟考试数学试题(已下线)2022年全国新高考Ⅰ卷数学试题变式题1-4题(已下线)考点03函数及其性质-3-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)(已下线)2022年全国新高考Ⅰ卷数学试题变式题9-12题浙江省百校联盟2022-2023学年高三上学期11月模拟数学试题
名校
解题方法
10 . 已知函数 ,则( )
,则( )
 ,则( )
,则( )A.当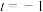 时, 时, 在 在 有最小值1 有最小值1 |
B.当 时, 时, 图象关于点 图象关于点 中心对称 中心对称 |
C.当 时, 时,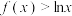 对任意 对任意 恒成立 恒成立 |
D. 至少有一个零点的充要条件是 至少有一个零点的充要条件是 |
您最近一年使用:0次
2023-03-01更新
|
1554次组卷
|
4卷引用:山东省淄博市2023届高三下学期一模数学试题
山东省淄博市2023届高三下学期一模数学试题福建省厦门市湖滨中学2022-2023学年高二下学期期中考试数学试题(已下线)第二章 函数的概念与性质 第二节 函数的单调性与最值(B素养提升卷)河南省周口市太康县第二高级中学2022-2023学年高二下学期3月月考数学试题



