专题14 导数的综合应用
【要点提炼】
1.利用导数研究函数的零点
函数的零点、方程的实根、函数图象与x轴的交点的横坐标是三个等价的概念,解决这类问题可以通过函数的单调性、极值与最值,画出函数图象的变化趋势,数形结合求解.
2.三次函数的零点分布
三次函数在存在两个极值点的情况下,由于当x→∞时,函数值也趋向∞,只要按照极值与零的大小关系确定其零点的个数即可.存在两个极值点x1,x2且x1<x2的函数f(x)=ax3+bx2+cx+d(a≠0)的零点分布情况如下:
a的符号 | 零点个数 | 充要条件 |
a>0 (f(x1)为极大值, f(x2)为极小值) | 一个 | f(x1)<0或f(x2)>0 |
两个 | f(x1)=0或f(x2)=0 | |
三个 | f(x1)>0且f(x2)<0 | |
a<0 (f(x1)为极小值, f(x2)为极大值) | 一个 | f(x1)>0或f(x2)<0 |
两个 | f(x1)=0或f(x2)=0 | |
三个 | f(x1)<0且f(x2)>0 |
3.利用导数解决不等式问题
(1)利用导数证明不等式.
若证明f(x)<g(x),x∈(a,b),可以构造函数F(x)=f(x)-g(x),如果能证明F(x)在(a,b)上的最大值小于0,即可证明f(x)<g(x),x∈(a,b).
(2)利用导数解决不等式的“恒成立”与“存在性”问题.
①f(x)>g(x)对一切x∈I恒成立⇔I是f(x)>g(x)的解集的子集⇔[f(x)-g(x)]min>0(x∈I).
②∃x∈I,使f(x)>g(x)成立⇔I与f(x)>g(x)的解集的交集不是空集⇔[f(x)-g(x)]max>0(x∈I).
③对∀x1,x2∈I使得f(x1)≤g(x2)⇔f(x)≤g(x)min.
④对∀x1∈I,∃x2∈I使得f(x1)≥g(x2)⇔f(x)min≥g(x)min.
4.(1)判断含x,ln x,ex的混合式的函数值的符号时,需利用x0=eln x0及ex≥x+1,ln x≤x-1对函数式放缩,有时可放缩为一个常量,变形为关于x的一次式或二次式,再判断符号.
(2)会对复杂函数式或导数式(如含x,ln x,ex的混合式)变形,如拆分为两个函数处理,好处是避免由于式子的复杂导致的思路无法开展.
考点
考向一 利用导数研究函数的零点
【典例1】 (2020·全国Ⅰ卷)已知函数f(x)=ex-a(x+2).
(1)当a=1时,讨论f(x)的单调性;
(2)若f(x)有两个零点,求a的取值范围.
解 (1)当a=1时,f(x)=ex-x-2,x∈R,则f′(x)=ex-1.
当x<0时,f′(x)<0;当x>0时,f′(x)>0.
所以f(x)在(-∞,0)单调递减,在(0,+∞)单调递增.
(2)f′(x)=ex-a.
①当a≤0时,f′(x)>0,
所以f(x)在(-∞,+∞)单调递增.
故f(x)至多存在一个零点,不合题意.
②当a>0时,由f′(x)=0,可得x=ln a.
当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
所以f(x)在(-∞,ln a)单调递减,在(ln a,+∞)单调递增.
故当x=ln a时,f(x)取得最小值,最小值为f(ln a)=-a(1+ln a).
(ⅰ)若0<a≤![]() ,则f(ln a)≥0,f(x)在(-∞,+∞)至多存在一个零点,不合题意.
,则f(ln a)≥0,f(x)在(-∞,+∞)至多存在一个零点,不合题意.
(ⅱ)若a>![]() ,则f(ln a)<0.
,则f(ln a)<0.
由于f(-2)=e-2>0,所以f(x)在(-∞,ln a)存在唯一零点.
由(1)知,当x>2时,ex-x-2>0.
所以当x>4且x>2ln (2a)时,f(x)=e![]() ·e
·e![]() -a(x+2)>eln (2a)·
-a(x+2)>eln (2a)·![]() -a(x+2)=2a>0.
-a(x+2)=2a>0.
故f(x)在(ln a,+∞)存在唯一零点.
从而f(x)在(-∞,+∞)有两个零点.
综上,a的取值范围是![]() .
.
探究提高 1.三步求解函数零点(方程根)的个数问题.
第一步:将问题转化为函数的零点问题,进而转化为函数的图象与x轴(或直线y=k)在该区间上的交点问题;
第二步:利用导数研究该函数在该区间上单调性、极值(最值)、端点值等性质;
第三步:结合图象求解.
2.已知零点求参数的取值范围:(1)结合图象与单调性,分析函数的极值点,(2)依据零点确定极值的范围,(3)对于参数选择恰当的分类标准进行讨论.
【拓展练习1】 设函数f(x)=ln x-a(x-1)ex,其中a∈R.
(1)若a≤0,讨论f(x)的单调性;
(2)若0<a<![]() ,试证明f(x)恰有两个零点.
,试证明f(x)恰有两个零点.
(1)解 由已知,f(x)的定义域为(0,+∞),且f′(x)=![]() -[aex+a(x-1)ex]=
-[aex+a(x-1)ex]=![]() .
.
因此当a≤0时,1-ax2ex>0,从而f′(x)>0,
所以f(x)在(0,+∞)内单调递增.
(2)证明 由(1)知,f′(x)=![]() .
.
令g(x)=1-ax2ex,
由0<a<![]() ,可知g(x)在(0,+∞)内单调递减.
,可知g(x)在(0,+∞)内单调递减.
又g(1)=1-ae>0,且
g![]() =1-a
=1-a![]()
![]() ·
·![]() =1-
=1-![]()
![]() <0,
<0,
故g(x)=0在(0,+∞)内有唯一解,
从而f′(x)=0在(0,+∞)内有唯一解,
不妨设为x0,则1<x0<ln ![]() .
.
当x∈(0,x0)时,f′(x)=![]() >
>![]() =0,
=0,
所以f(x)在(0,x0)内单调递增;
当x∈(x0,+∞)时,f′(x)=![]() <
<![]() =0,
=0,
所以f(x)在(x0,+∞)内单调递减,
因此x0是f(x)的唯一极值点.
令h(x)=ln x-x+1,
则当x>1时,h′(x)=![]() -1<0,
-1<0,
故h(x)在(1,+∞)内单调递减,
从而当x>1时,h(x)<h(1)=0,
所以ln x<x-1,
从而f![]() =ln
=ln ![]() -a
-a![]() eln
eln ![]()
=ln ![]() -ln
-ln ![]() +1=h
+1=h![]() <0.
<0.
又因为f(x0)>f(1)=0,
所以f(x)在(x0,+∞)内有唯一零点.
又f(x)在(0,x0)内有唯一零点1,
从而,f(x)在(0,+∞)内恰有两个零点.
考向二 利用导数证明不等式
【典例2】 (2020·衡水中学检测)已知函数f(x)=ln ![]() .
.
(1)求证:当x∈(0,1)时,f(x)>2![]() ;
;
(2)设实数k使得f(x)>k![]() 对x∈(0,1)恒成立,求k的最大值.
对x∈(0,1)恒成立,求k的最大值.
(1)证明 令g(x)=f(x)-2![]() ,则
,则
g′(x)=f′(x)-2(1+x2)=![]() .
.
因为g′(x)>0(0<x<1),所以g(x)在区间(0,1)上单调递增.
所以g(x)>g(0)=0,x∈(0,1),
即当x∈(0,1)时,f(x)>2![]() .
.
(2)解 由(1)知,当k≤2时,f(x)>k![]() 对x∈(0,1)恒成立.
对x∈(0,1)恒成立.
当k>2时,令h(x)=f(x)-k![]() ,则
,则
h′(x)=f′(x)-k(1+x2)=![]() .
.
所以当0<x<![]() 时,h′(x)<0,因此h(x)在区间
时,h′(x)<0,因此h(x)在区间![]() 上单调递减.
上单调递减.
当0<x<![]() 时,h(x)<h(0)=0,
时,h(x)<h(0)=0,
即f(x)<k![]() .
.
所以当k>2时,f(x)>k![]() 并非对x∈(0,1)恒成立.
并非对x∈(0,1)恒成立.
综上可知,k的最大值为2.
探究提高 形如f(x)>g(x)的不等式的证明:(1)首先构造函数h(x)=f(x)-g(x),借助导数求h(x)min,证明h(x)min>0.(2)如果不等式既有指数又有对数,求导不易求最值,可合理分拆和变形,构造两个函数,分别计算它们的最值,利用隔离分析最值法证明.
【拓展练习2】 (2020·岳阳二模)已知函数f(x)=x-ln x-![]() .
.
(1)求证:f(x)≤1-e;
(2)若f(x)+![]() ex-bx≥1恒成立,求实数b的取值范围.
ex-bx≥1恒成立,求实数b的取值范围.
(1)证明 f(x)=x-ln x-![]() ,定义域为(0,+∞),
,定义域为(0,+∞),
则f′(x)=1-![]() -
-![]() =
=![]() ,
,
由ex≥x+1>x,知0<x<1时,f′(x)>0;x>1时,f′(x)<0,
得f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以f(x)max=f(1)=1-e.从而f(x)≤1-e.
(2)解 f(x)+![]() ex-bx≥1,即-ln x+x-
ex-bx≥1,即-ln x+x-![]() +xex+
+xex+![]() -bx≥1,
-bx≥1,
恒有![]() ≥b,即
≥b,即![]()
![]() ≥b.
≥b.
令φ(x)=![]() ,则φ′(x)=
,则φ′(x)=![]() ,
,
令h(x)=x2ex+ln x,则h(x)在(0,+∞)上单调递增,
因为x→0时,h(x)→-∞,h(1)=e>0,
所以h(x)在(0,1)上存在唯一零点x0,且h(x0)=x![]() ex0+ln x0=0,
ex0+ln x0=0,
所以x0ex0=-![]() =
=![]() (eln
(eln ![]() ).
).
令m(x)=xex,上式即m(x0)=m![]() .
.
由于m(x)=xex在(0,+∞)上单调递增,
故x0=ln![]() =-lnx0,即ex0=
=-lnx0,即ex0=![]() ,
,
从而φ′(x0)=0且0<x<x0时,h(x)<0,φ′(x)<0;x>x0时,h(x)>0,φ′(x)>0,
所以φ(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,
φ(x)min=φ(x0)=![]() =
=![]() =2,
=2,
所以b≤2.即实数b的取值范围为(-∞,2].
考向三 导数与不等式恒成立、存在性问题
角度1 含参不等式的恒成立问题
【典例3】 已知函数f(x)=x2+4x+2,g(x)=2ex(x+1).若x≥-2时,f(x)≤kg(x),求k的取值范围.
解 设函数F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2,则F′(x)=2kex(x+2)-2x-4
=2(x+2)(kex-1).
由题设可得F(0)≥0,即k≥1.
令F′(x)=0,得x1=-ln k,x2=-2.
(ⅰ)若1≤k<e2,则-2<x1≤0.
从而当x∈(-2,x1)时,F′(x)<0;
当x∈(x1,+∞)时,F′(x)>0.即F(x)在(-2,x1)上单调递减,在(x1,+∞)上单调递增.故F(x)在[-2,+∞)上的最小值为F(x1).
而F(x1)=2x1+2-x![]() -4x1-2=-x1(x1+2)≥0.
-4x1-2=-x1(x1+2)≥0.
故当x≥-2时,F(x)≥0,
即f(x)≤kg(x)恒成立.
(ⅱ)若k=e2,则F′(x)=2e2(x+2)(ex-e-2).
从而当x>-2时,F′(x)>0,
即F(x)在(-2,+∞)上单调递增.
而F(-2)=0,故当x≥-2时,F(x)≥0,
即F(x)≤kg(x)恒成立.
(ⅲ)若k>e2,则F(-2)=-2ke-2+2=-2e-2(k-e2)<0.从而当x≥-2时,f(x)≤kg(x)不可能恒成立.
综上,k的取值范围是[1,e2].
探究提高 1.此类问题要根据导数式的特点对参数进行讨论,在每个范围内由单调性得到最值,利用最值来判断是否满足题意,说明不满足题意时,只需举一反典例即可.
2.x,ex,ln x组合型函数问题,解题思路有两个关键方向:一是要充分考虑指数式与对数式的运算性质的应用,如![]() =eln
=eln ![]() 是N=alogaN(a>0,a≠1)的应用,x0=ln
是N=alogaN(a>0,a≠1)的应用,x0=ln ![]() 化为ex0=
化为ex0=![]() 是指数式与对数式互化的应用;二是要考虑能否运用不等式放缩转化目标,如利用ex≥x+1,从而快速解不等式,得到函数的单调区间.
是指数式与对数式互化的应用;二是要考虑能否运用不等式放缩转化目标,如利用ex≥x+1,从而快速解不等式,得到函数的单调区间.
【拓展练习3】 设函数f(x)=ax2-a-ln x,其中a∈R.
(1)讨论f(x)的单调性;
(2)确定a的所有可能取值,使得f(x)>![]() -e1-x在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
-e1-x在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
解 (1)f′(x)=2ax-![]() =
=![]() (x>0).
(x>0).
当a≤0时,f′(x)<0,f(x)在(0,+∞)内单调递减.
当a>0时,由f′(x)=0,有x=![]() .
.
此时,当x∈![]() 时,f′(x)<0,f(x)单调递减;
时,f′(x)<0,f(x)单调递减;
当x∈![]() 时,f′(x)>0,f(x)单调递增.
时,f′(x)>0,f(x)单调递增.
(2)令g(x)=![]() -
-![]() ,s(x)=ex-1-x.
,s(x)=ex-1-x.
则s′(x)=ex-1-1.
而当x>1时,s′(x)>0,
所以s(x)在区间(1,+∞)内单调递增.
又由s(1)=0,有s(x)>0,从而当x>1时,g(x)>0.
当a≤0,x>1时,f(x)=a(x2-1)-ln x<0.
故当f(x)>g(x)在区间(1,+∞)内恒成立时,必有a>0.
当0<a<![]() 时,
时,![]() >1.
>1.
由(1)有f![]() <f(1)=0,而g
<f(1)=0,而g![]() >0,
>0,
所以此时f(x)>g(x)在区间(1,+∞)内不恒成立.
当a≥![]() 时,令h(x)=f(x)-g(x)(x≥1).
时,令h(x)=f(x)-g(x)(x≥1).
当x>1时,h′(x)=2ax-![]() +
+![]() -e1-x>x-
-e1-x>x-![]() +
+![]() -
-![]() =
=![]() >
>![]() >0.
>0.
因此,h(x)在区间(1,+∞)单调递增.
又因为h(1)=0,所以当x>1时,h(x)=f(x)-g(x)>0,即f(x)>g(x)恒成立.
综上,a∈![]() .
.
角度2 不等式存在性问题
【典例4】 设函数f(x)=aln x+![]() x2-x(a≠1).若存在x0≥1,使得f(x0)<
x2-x(a≠1).若存在x0≥1,使得f(x0)<![]() ,求a的取值范围.
,求a的取值范围.
解 f(x)的定义域为(0,+∞),
因为f(x)=aln x+![]() x2-x,
x2-x,
f′(x)=![]() +(1-a)x-1=
+(1-a)x-1=![]()
![]() (x-1).
(x-1).
①若a≤![]() ,则
,则![]() ≤1,故当x∈(1,+∞)时,
≤1,故当x∈(1,+∞)时,
f′(x)>0,f(x)在(1,+∞)上单调递增.
所以,存在x0≥1,使得f(x0)<![]() 成立的充要条件为
成立的充要条件为
f(1)<![]() ,即
,即![]() -1<
-1<![]() ,解得-
,解得-![]() -1<a<
-1<a<![]() -1.
-1.
②若![]() <a<1,则
<a<1,则![]() >1,
>1,
故当x∈![]() 时,f′(x)<0;
时,f′(x)<0;
当x∈![]() 时,f′(x)>0.
时,f′(x)>0.
f(x)在![]() 上单调递减,
上单调递减,
在![]() 上单调递增.所以,存在x0≥1,
上单调递增.所以,存在x0≥1,
使得f(x0)<![]() 成立的充要条件为f
成立的充要条件为f![]() <
<![]() .
.
而f![]() =aln
=aln ![]() +
+![]() +
+![]() >
>![]() ,
,
所以不合题意.
③若a>1,f(x)在[1,+∞)上递减,
则f(1)=![]() -1=
-1=![]() <
<![]() .
.
综上,a的取值范围是(-![]() -1,
-1,![]() -1)∪(1,+∞).
-1)∪(1,+∞).
探究提高 “恒成立”与“存在性”问题的求解是“互补”关系,即f(x)≥g(a)对于x∈D恒成立,应求f(x)的最小值;若存在x∈D,使得f(x)≥g(a)成立,应求f(x)的最大值.应特别关注等号是否取到,注意端点的取舍.
【拓展练习4】 已知函数f(x)=x-mln x-![]() (m∈R),g(x)=
(m∈R),g(x)=![]() x2+ex-xex.
x2+ex-xex.
(1)当x∈[1,e]时,求f(x)的最小值;
(2)当m≤2时,若存在x1∈[e,e2],使得对任意的x2∈[-2,0],f(x1)≤g(x2)成立,求实数m的取值范围.
解 (1)f(x)=x-mln x-![]() ,且定义域(0,+∞),
,且定义域(0,+∞),
∴f′(x)=1-![]() +
+![]() =
=![]() ,
,
当m≤2时,若x∈[1,e],则f′(x)≥0,
∴f(x)在[1,e]上是增函数,则f(x)min=f(1)=2-m.
当m≥e+1时,若x∈[1,e],则f′(x)≤0,
∴f(x)在[1,e]上是减函数,
则f(x)min=f(e)=e-m-![]() .
.
当2<m<e+1时,若x∈[1,m-1],则f′(x)≤0;
若x∈[m-1,e],则f′(x)≥0.
f(x)min=f(m-1)=m-2-mln (m-1).
(2)已知等价于f(x1)min≤g(x2)min.
由(1)知m≤2时,在x∈[e,e2]上有f′(x)≥0,
∴f(x1)min=f(e)=e-m-![]() .
.
又g′(x)=x+ex-(x+1)ex=x(1-ex),
当x2∈[-2,0]时,g′(x2)≤0,g(x2)min=g(0)=1.
所以m≤2且e-m-![]() ≤1,解得
≤1,解得![]() ≤m≤2.
≤m≤2.
所以实数m的取值范围是![]() .
.
【专题拓展练习】
一、单选题
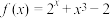 在区间(0,1)内的零点个数是
在区间(0,1)内的零点个数是| A.0 | B.1 |
| C.2 | D.3 |
【知识点】 零点存在性定理的应用 利用导数研究函数的零点
 的导函数
的导函数 ,则下列结论正确的是
,则下列结论正确的是A. 在 在 处有极大值 处有极大值 | B. 在 在 处有极小值 处有极小值 |
C. 在 在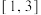 上单调递减 上单调递减 | D. 至少有3个零点 至少有3个零点 |
 ,对
,对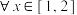 都有
都有 成立,则实数
成立,则实数 的取值范围是( )
的取值范围是( )A. | B. | C. | D.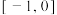 |
【知识点】 利用导数研究不等式恒成立问题
 是奇函数,当
是奇函数,当 时,
时,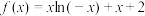 ,则曲线
,则曲线 在
在 处的切线方程为
处的切线方程为A.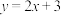 | B. | C.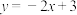 | D.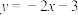 |
【知识点】 求在曲线上一点处的切线方程(斜率)
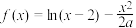 ,(
,( 为常数,且
为常数,且 ),若
),若 在
在 处取得极值,且
处取得极值,且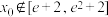 ,而
,而 在
在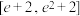 上恒成立,则
上恒成立,则 的取值范围是( )
的取值范围是( )A. | B.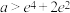 |
C. | D.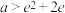 |
【知识点】 根据极值求参数 利用导数研究不等式恒成立问题
 与
与 ,若存在
,若存在 ,使
,使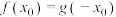 ,则称
,则称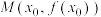 ,
,
 是函数
是函数 与
与 图象的一对“隐对称点”.已知函数
图象的一对“隐对称点”.已知函数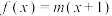 ,
,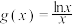 ,函数
,函数 与
与 的图象恰好存在两对“隐对称点”,则实数
的图象恰好存在两对“隐对称点”,则实数 的取值范围为( )
的取值范围为( )A.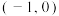 | B.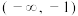 | C.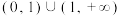 | D.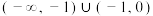 |
【知识点】 根据函数零点的个数求参数范围 利用导数研究函数的零点
 ,
,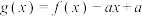 ,若
,若 恰有1个零点,则
恰有1个零点,则 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
 的大致图象如图所示,则
的大致图象如图所示,则 等于
等于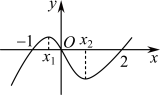
A.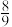 | B. | C.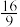 | D.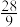 |
【知识点】 利用导数研究函数图象及性质
 的不等式
的不等式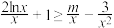 对任意的
对任意的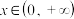 恒成立的实数
恒成立的实数 的取值集合为
的取值集合为 ,函数
,函数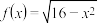 的值域为
的值域为 ,则有
,则有A. | B.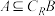 | C. | D.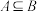 |
【知识点】 判断两个集合的包含关系解读 利用导数研究不等式恒成立问题
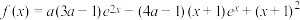 ,若函数
,若函数 图像与
图像与 轴有4个不同的交点,则实数
轴有4个不同的交点,则实数 的取值范围为( )
的取值范围为( )A.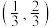 | B. |
C. | D.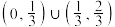 |
【知识点】 根据函数零点的个数求参数范围 利用导数研究函数图象及性质
 ,
, 为自然对数的底数,函数
为自然对数的底数,函数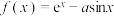 在
在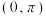 内有且仅有一个零点,则
内有且仅有一个零点,则 ( )
( )A.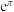 | B. | C.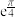 | D.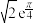 |
【知识点】 利用导数研究函数的零点
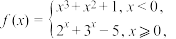 若函数
若函数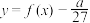 恰有3个零点,则满足条件的整数a的个数为( )
恰有3个零点,则满足条件的整数a的个数为( )| A.1 | B.2 | C.3 | D.4 |
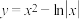 的图象大致为( )
的图象大致为( )A. | B. |
C. | D. |
【知识点】 函数图像的识别 利用导数研究函数图象及性质
二、解答题
 .
.(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)求证:当
 时,
时, .
.
【知识点】 利用导数求函数的单调区间(不含参) 利用导数证明不等式
 (aÎR).
(aÎR).(Ⅰ)当a=2时,求函数
 在(1, f(1))处的切线方程;
在(1, f(1))处的切线方程;(Ⅱ)当a>0时,求函数
 的单调区间;
的单调区间;(Ⅲ)若函数
 有两个极值点
有两个极值点 ,
,  (
(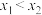 ),不等式
),不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【知识点】 函数单调性、极值与最值的综合应用 导数在函数中的其他应用


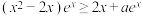 对
对 恒成立,则实数
恒成立,则实数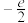
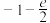
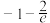
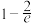
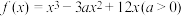 存在两个极值点
存在两个极值点 的取值范围是(
的取值范围是(
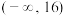
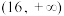

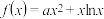 .
. ,求函数
,求函数 的在
的在 处的切线方程;
处的切线方程;  ,证明:方程
,证明:方程 无解.
无解.


