1 . 下列可以成为不等式“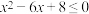 ”成立的必要不充分条件的有
”成立的必要不充分条件的有________________ .(填序号)
①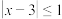 ;②
;② ③
③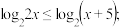 ④
④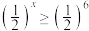 .
.
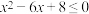 ”成立的必要不充分条件的有
”成立的必要不充分条件的有①
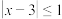 ;②
;② ③
③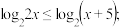 ④
④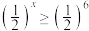 .
.
您最近一年使用:0次
名校
2 . 如图曲线E:可以看成是抛物线 和
和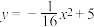 所围成示,点M,N在曲线E上,给定点
所围成示,点M,N在曲线E上,给定点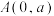 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
 和
和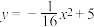 所围成示,点M,N在曲线E上,给定点
所围成示,点M,N在曲线E上,给定点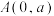 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.任意 ,都存在点M,N,使得 ,都存在点M,N,使得 |
B.任意 ,都存在点M,N,满足这对点关于点A对称 ,都存在点M,N,满足这对点关于点A对称 |
C.存在 ,当点M,N运动时,使得 ,当点M,N运动时,使得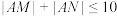 |
D.任意 ,恰有三对不同的点M,N,满足每对点M,N关于点A对称 ,恰有三对不同的点M,N,满足每对点M,N关于点A对称 |
您最近一年使用:0次
名校
解题方法
3 . 设函数 .
.
(1)若不等式 的解集为
的解集为 ,求
,求 的取值范围;
的取值范围;
(2)当 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;
(3)对于任意的 ,不等式
,不等式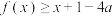 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)若不等式
 的解集为
的解集为 ,求
,求 的取值范围;
的取值范围;(2)当
 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;(3)对于任意的
 ,不等式
,不等式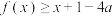 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
594次组卷
|
2卷引用:安徽省合肥市合肥一六八中学2024-2025学年高一上学期第二次月考数学试题
名校
解题方法
4 . 命题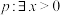 ,
,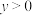 ,使得不等式
,使得不等式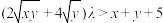 成立,下列不是命题
成立,下列不是命题 成立的充分不必要条件的是( )
成立的充分不必要条件的是( )
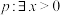 ,
,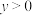 ,使得不等式
,使得不等式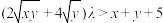 成立,下列不是命题
成立,下列不是命题 成立的充分不必要条件的是( )
成立的充分不必要条件的是( )A.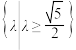 | B.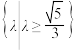 |
C.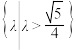 | D.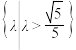 |
您最近一年使用:0次
名校
5 . 已知关于 的一元二次不等式
的一元二次不等式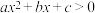 的解集为
的解集为 ,则下列说法错误的是( )
,则下列说法错误的是( )
 的一元二次不等式
的一元二次不等式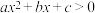 的解集为
的解集为 ,则下列说法错误的是( )
,则下列说法错误的是( )A.若 ,则 ,则 且 且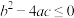 |
B.若 ,则关于 ,则关于 的不等式 的不等式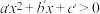 的解集也为 的解集也为 |
C.若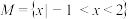 ,则关于 ,则关于 的不等式 的不等式 的解集为 的解集为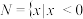 或 或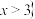 |
D.若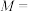 { {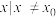 , , 为常数 为常数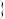 ,且 ,且 ,则 ,则 的最小值为 的最小值为 |
您最近一年使用:0次
名校
6 . 已知函数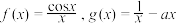 .
.
(1)若函数 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(2)若函数 和函数
和函数 的图象没有公共点,求实数
的图象没有公共点,求实数 的取值范围.
的取值范围.
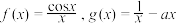 .
.(1)若函数
 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;(2)若函数
 和函数
和函数 的图象没有公共点,求实数
的图象没有公共点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-10-25更新
|
225次组卷
|
2卷引用:安徽省合肥市第一中学2024-2025学年高三上学期第三次素质拓展数学试题
名校
解题方法
7 . 若函数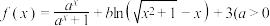 且
且 为常数
为常数 在
在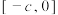 (
( 为常数)上有最小值
为常数)上有最小值 ,则
,则 在
在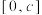 上( )
上( )
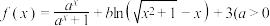 且
且 为常数
为常数 在
在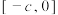 (
( 为常数)上有最小值
为常数)上有最小值 ,则
,则 在
在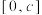 上( )
上( )| A.有最大值12 | B.有最大值6 |
C.有最小值 | D.有最小值 |
您最近一年使用:0次
2024-10-24更新
|
637次组卷
|
2卷引用:安徽省合肥市第四中学2025届高三上学期教学诊断检测(三)数学试题
名校
8 . 已知函数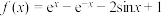 ,不等式
,不等式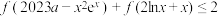 对任意的
对任意的 恒成立,则
恒成立,则 的最大值为
的最大值为___________ .
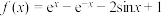 ,不等式
,不等式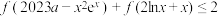 对任意的
对任意的 恒成立,则
恒成立,则 的最大值为
的最大值为
您最近一年使用:0次
名校
9 . 当一个函数值域内任意一个函数值y都有且只有一个自变量x与之对应时,可以把这个函数的函数值y作为一个新的函数的自变量,而这个函数的自变量x作为新的函数的函数值,我们称这两个函数互为反函数.例如,由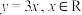 ,得
,得 ,通常用x表示自变量,则写成
,通常用x表示自变量,则写成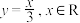 ,我们称
,我们称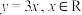 与
与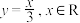 互为反函数.已知函数
互为反函数.已知函数 与
与 互为反函数,若
互为反函数,若 两点在曲线
两点在曲线 上,
上, 两点在曲线
两点在曲线 上,以
上,以 四点为顶点构成的四边形为矩形,且该矩形的其中一条边与直线
四点为顶点构成的四边形为矩形,且该矩形的其中一条边与直线 垂直,则我们称这个矩形为
垂直,则我们称这个矩形为 与
与 的“关联矩形”.
的“关联矩形”.
(1)若函数 ,且点
,且点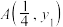 在曲线
在曲线 上,求以点
上,求以点 为一个顶点的“关联矩形”的面积.
为一个顶点的“关联矩形”的面积.
(2)若函数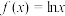 ,且
,且 与
与 的“关联矩形”是正方形,记该“关联矩形”的面积为
的“关联矩形”是正方形,记该“关联矩形”的面积为 .证明:
.证明: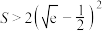 .(参考数据:
.(参考数据: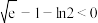 )
)
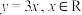 ,得
,得 ,通常用x表示自变量,则写成
,通常用x表示自变量,则写成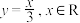 ,我们称
,我们称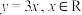 与
与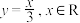 互为反函数.已知函数
互为反函数.已知函数 与
与 互为反函数,若
互为反函数,若 两点在曲线
两点在曲线 上,
上, 两点在曲线
两点在曲线 上,以
上,以 四点为顶点构成的四边形为矩形,且该矩形的其中一条边与直线
四点为顶点构成的四边形为矩形,且该矩形的其中一条边与直线 垂直,则我们称这个矩形为
垂直,则我们称这个矩形为 与
与 的“关联矩形”.
的“关联矩形”.(1)若函数
 ,且点
,且点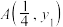 在曲线
在曲线 上,求以点
上,求以点 为一个顶点的“关联矩形”的面积.
为一个顶点的“关联矩形”的面积.(2)若函数
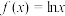 ,且
,且 与
与 的“关联矩形”是正方形,记该“关联矩形”的面积为
的“关联矩形”是正方形,记该“关联矩形”的面积为 .证明:
.证明: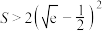 .(参考数据:
.(参考数据: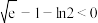 )
)
您最近一年使用:0次
名校
解题方法
10 . 已知函数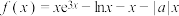 ,若对任意的
,若对任意的 ,
,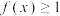 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
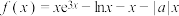 ,若对任意的
,若对任意的 ,
,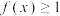 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )A.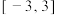 | B. | C.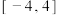 | D. |
您最近一年使用:0次
2024-10-23更新
|
443次组卷
|
4卷引用:安徽省六校2025届高三上学期第一次阶段联合教学质量测评数学试卷



