1 . 已知函数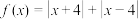 .
.
(Ⅰ)求不等式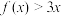 的解集;
的解集;
(Ⅱ)设函数 的最小值为
的最小值为 ,正实数
,正实数 ,
, 满足
满足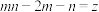 ,求证:
,求证: .
.
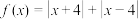 .
.(Ⅰ)求不等式
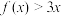 的解集;
的解集;(Ⅱ)设函数
 的最小值为
的最小值为 ,正实数
,正实数 ,
, 满足
满足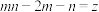 ,求证:
,求证: .
.
您最近一年使用:0次
名校
2 . 已知数列 ,满足
,满足 ,
,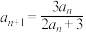 ,
, .
.
(1)求证:数列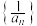 为等差数列;
为等差数列;
(2)设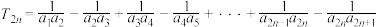 ,求
,求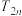 .
.
 ,满足
,满足 ,
,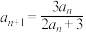 ,
, .
.(1)求证:数列
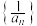 为等差数列;
为等差数列;(2)设
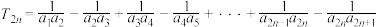 ,求
,求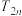 .
.
您最近一年使用:0次
2020-04-27更新
|
398次组卷
|
2卷引用:新疆博尔塔拉蒙古自治州第五师高级中学2019-2020学年高三上学期第二次月考数学(理)试题
名校
3 . 已知函数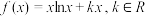 .
.
(1)求 在点
在点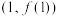 处的切线方程;
处的切线方程;
(2)若不等式 恒成立,求k的取值范围;
恒成立,求k的取值范围;
(3)求证:当 时,不等式
时,不等式 成立.
成立.
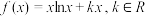 .
.(1)求
 在点
在点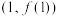 处的切线方程;
处的切线方程;(2)若不等式
 恒成立,求k的取值范围;
恒成立,求k的取值范围;(3)求证:当
 时,不等式
时,不等式 成立.
成立.
您最近一年使用:0次
2020-02-05更新
|
1185次组卷
|
9卷引用:2020届辽宁省葫芦岛市普通高中高三上学期学业质量监测(期末)数学(理)试题
2020届辽宁省葫芦岛市普通高中高三上学期学业质量监测(期末)数学(理)试题2020届高三2月第02期(考点03)(理科)-《新题速递·数学》2020届山东省潍坊市高三2月数学模拟试题(二)(已下线)备战2020年高考数学之考场再现(山东专版)03(已下线)第4篇——函数导数及其应用-新高考山东专题汇编山东省淄博市临淄中学2020-2021学年高三上学期期中数学试题广东省广东实验中学2022届高三上学期九月阶段测试数学试题黑龙江省牡丹江市第一高级中学2022-2023学年高三上学期期中考试数学试题吉林省长春市文理高中2025届高三上学期校二模考试数学试题
名校
4 . 已知函数 ,
,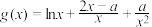 .
.
(1)求证: 在区间
在区间 上有且仅有一个零点
上有且仅有一个零点 ,且
,且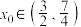 ;
;
(2)若当 时,不等式
时,不等式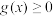 恒成立,求证:
恒成立,求证: .
.
 ,
,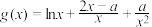 .
.(1)求证:
 在区间
在区间 上有且仅有一个零点
上有且仅有一个零点 ,且
,且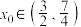 ;
;(2)若当
 时,不等式
时,不等式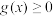 恒成立,求证:
恒成立,求证: .
.
您最近一年使用:0次
名校
5 . 已知函数 ,
, 的定义域分别为
的定义域分别为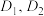 ,若存在常数
,若存在常数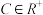 ,满足:①对任意
,满足:①对任意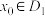 ,恒有
,恒有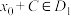 ,且
,且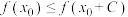 .②对任意
.②对任意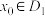 ,关于
,关于 的不等式组
的不等式组
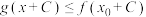 恒有解,则称
恒有解,则称 为
为 的一个“
的一个“ 型函数”.
型函数”.
(1)设函数 和
和 ,求证:
,求证: 为
为 的一个“
的一个“ 型函数”;
型函数”;
(2)设常数 ,函数
,函数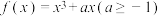 ,
,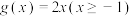 .若
.若 为
为 的一个“
的一个“ 型函数”,求
型函数”,求 的取值范围;
的取值范围;
(3)设函数 .问:是否存在常数
.问:是否存在常数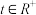 ,使得函数
,使得函数 为
为 的一个“
的一个“ 型函数”?若存在,求
型函数”?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
 ,
, 的定义域分别为
的定义域分别为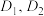 ,若存在常数
,若存在常数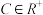 ,满足:①对任意
,满足:①对任意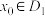 ,恒有
,恒有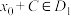 ,且
,且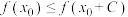 .②对任意
.②对任意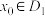 ,关于
,关于 的不等式组
的不等式组
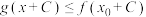 恒有解,则称
恒有解,则称 为
为 的一个“
的一个“ 型函数”.
型函数”.(1)设函数
 和
和 ,求证:
,求证: 为
为 的一个“
的一个“ 型函数”;
型函数”;(2)设常数
 ,函数
,函数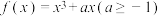 ,
,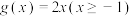 .若
.若 为
为 的一个“
的一个“ 型函数”,求
型函数”,求 的取值范围;
的取值范围;(3)设函数
 .问:是否存在常数
.问:是否存在常数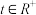 ,使得函数
,使得函数 为
为 的一个“
的一个“ 型函数”?若存在,求
型函数”?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
您最近一年使用:0次
名校
解题方法
6 . 已知椭圆E: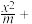 y2=1(m>1)的离心率为
y2=1(m>1)的离心率为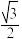 ,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
(Ⅰ)求m的值;
(Ⅱ)求证:直线A0B恒过定点.
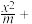 y2=1(m>1)的离心率为
y2=1(m>1)的离心率为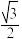 ,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.(Ⅰ)求m的值;
(Ⅱ)求证:直线A0B恒过定点.
您最近一年使用:0次
解题方法
7 . 已知函数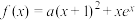 ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数.
(1)若函数 既有极大值又有极小值,试求实数
既有极大值又有极小值,试求实数 的取值范围;
的取值范围;
(2)设 ,且
,且 ,
, 是函数
是函数 的两个零点,求证:
的两个零点,求证: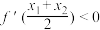 .
.
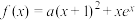 ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数.(1)若函数
 既有极大值又有极小值,试求实数
既有极大值又有极小值,试求实数 的取值范围;
的取值范围;(2)设
 ,且
,且 ,
, 是函数
是函数 的两个零点,求证:
的两个零点,求证: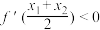 .
.
您最近一年使用:0次
名校
解题方法
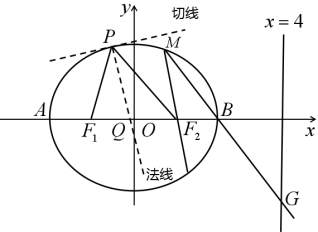
8 . 如图,椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.已知椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,左、右顶点分别为
,左、右顶点分别为 ,
, ,一光线从点
,一光线从点 射出经椭圆
射出经椭圆 上
上 点反射,法线(与椭圆
点反射,法线(与椭圆 在
在 处的切线垂直的直线)与
处的切线垂直的直线)与 轴交于点
轴交于点 ,已知
,已知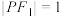 ,
,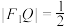 .
.
(1)求椭圆 的方程.
的方程.
(2)过 的直线与椭圆
的直线与椭圆 交于
交于 ,
, 两点(均不与
两点(均不与 ,
, 重合),直线
重合),直线 与直线
与直线 交于
交于 点,证明:
点,证明: ,
, ,
, 三点共线.
三点共线.
 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,左、右顶点分别为
,左、右顶点分别为 ,
, ,一光线从点
,一光线从点 射出经椭圆
射出经椭圆 上
上 点反射,法线(与椭圆
点反射,法线(与椭圆 在
在 处的切线垂直的直线)与
处的切线垂直的直线)与 轴交于点
轴交于点 ,已知
,已知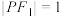 ,
,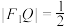 .
.
(1)求椭圆
 的方程.
的方程.(2)过
 的直线与椭圆
的直线与椭圆 交于
交于 ,
, 两点(均不与
两点(均不与 ,
, 重合),直线
重合),直线 与直线
与直线 交于
交于 点,证明:
点,证明: ,
, ,
, 三点共线.
三点共线.
您最近一年使用:0次
2021-05-01更新
|
639次组卷
|
4卷引用:广东省广州市协和中学2020-2021学年高二上学期期中数学试题
名校
解题方法
9 . 已知椭圆 的左、右焦点为
的左、右焦点为 ,左右两顶点
,左右两顶点 ,点
,点 为椭圆
为椭圆 上任意一点,满足直线
上任意一点,满足直线 的斜率之积为
的斜率之积为 ,且
,且 的最大值为4.
的最大值为4.
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线 与过点
与过点 且与
且与 轴垂直的直线交于点
轴垂直的直线交于点 ,过点
,过点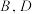 作
作 ,垂足分别为
,垂足分别为 两点,求证:
两点,求证: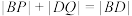 .
.
 的左、右焦点为
的左、右焦点为 ,左右两顶点
,左右两顶点 ,点
,点 为椭圆
为椭圆 上任意一点,满足直线
上任意一点,满足直线 的斜率之积为
的斜率之积为 ,且
,且 的最大值为4.
的最大值为4.(1)求椭圆
 的标准方程;
的标准方程;(2)若直线
 与过点
与过点 且与
且与 轴垂直的直线交于点
轴垂直的直线交于点 ,过点
,过点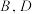 作
作 ,垂足分别为
,垂足分别为 两点,求证:
两点,求证: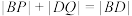 .
.
您最近一年使用:0次
解题方法
10 . 已知定义域为 的函数
的函数 是奇函数.
是奇函数.
(1)求 、
、 的值;
的值;
(2)判断 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;
(3)若对任意的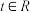 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的函数
的函数 是奇函数.
是奇函数.(1)求
 、
、 的值;
的值;(2)判断
 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;(3)若对任意的
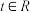 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-09-10更新
|
169次组卷
|
7卷引用:2016-2017学年广西陆川县中学高一9月月考数学试试卷
2016-2017学年广西陆川县中学高一9月月考数学试试卷2016-2017学年广西陆川县中学高一9月月考数学试卷四川省资阳市乐至县良安中学2019-2020学年高一上学期期中数学试题(已下线)专题09 函数的单调性、奇偶性、周期性与对称性综合练习-2021年高考一轮数学(理)单元复习一遍过(已下线)专题09 函数的单调性、奇偶性、周期性与对称性综合练习-2021年高考一轮数学(文)单元复习一遍过(已下线)专题09 函数的单调性、奇偶性、周期性与对称性综合练习-2021年高考一轮数学单元复习一遍过(新高考地区专用)人教B版(2019) 必修第二册 学习帮手 模块检测



