21.

年五一节期间,我国高速公路继续执行“节假日高速公路免费政策”.某路桥公司为掌握五一节期间车辆出行的高峰情况,在某高速公路收费站点记录了

日上午

这一时间段内通过的车辆数,统计发现这一时间段内共有

辆车通过该收费站点,它们通过该收费站点的时刻的频率分布直方图如下图所示,其中时间段

记作

,

记作
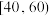
,

记作
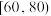
,

记作

,例如:
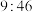
,记作时刻

.
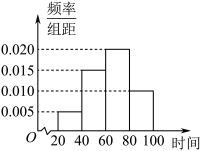
(1)估计这

辆车在

时间内通过该收费站点的时刻的平均值(同一组中的数据用该组区间的中点值代替)
(2)为了对数据进行分析,现采用分层抽样的方法从这

辆车中抽取

辆,再从这

辆车中随机抽取

辆,设抽到的

辆车中,在

之间通过的车辆数为

,求

的分布列;
(3)根据大数据分析,车辆在每天通过该收费站点的时刻

服从正态分布

,其中

可用

日数据中的

辆车在

之间通过该收费站点的时刻的平均值近似代替,

用样本的方差近似代替(经计算样本方差为
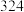
).假如

日上午

这一时间段内共有

辆车通过该收费站点,估计在

之间通过的车辆数(结果保留到整数)
附:

;若随机变量

服从正态分布

,则
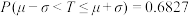
,
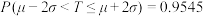
,
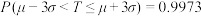
.