1 . 设抛物线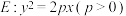 的焦点为
的焦点为 ,过
,过 且斜率为1的直线与
且斜率为1的直线与 交于
交于 两点,且
两点,且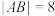 .
.
(1)求抛物线 的方程;
的方程;
(2)已知过点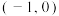 的直线
的直线 与
与 交于不重合的两点
交于不重合的两点 ,且
,且 ,直线
,直线 和
和 的斜率分别为
的斜率分别为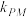 和
和 .求证:
.求证: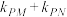 为定值.
为定值.
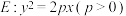 的焦点为
的焦点为 ,过
,过 且斜率为1的直线与
且斜率为1的直线与 交于
交于 两点,且
两点,且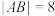 .
.(1)求抛物线
 的方程;
的方程;(2)已知过点
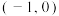 的直线
的直线 与
与 交于不重合的两点
交于不重合的两点 ,且
,且 ,直线
,直线 和
和 的斜率分别为
的斜率分别为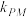 和
和 .求证:
.求证: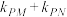 为定值.
为定值.
您最近一年使用:0次
2024-01-03更新
|
736次组卷
|
4卷引用:广西壮族自治区玉林市博白县五校2023-2024学年高二上学期12月联考数学试卷
名校
解题方法
2 . 已知椭圆 ,焦距为2,离心率
,焦距为2,离心率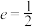 .
.
(1)求椭圆 的方程;
的方程;
(2)若椭圆 的左焦点为
的左焦点为 ,椭圆上A点横坐标为
,椭圆上A点横坐标为 ,求椭圆的长轴长、短轴长及
,求椭圆的长轴长、短轴长及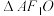 的面积
的面积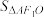 .
.
 ,焦距为2,离心率
,焦距为2,离心率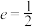 .
.(1)求椭圆
 的方程;
的方程;(2)若椭圆
 的左焦点为
的左焦点为 ,椭圆上A点横坐标为
,椭圆上A点横坐标为 ,求椭圆的长轴长、短轴长及
,求椭圆的长轴长、短轴长及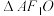 的面积
的面积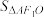 .
.
您最近一年使用:0次
2024-01-03更新
|
3374次组卷
|
5卷引用:广西壮族自治区玉林市博白县五校2023-2024学年高二上学期12月联考数学试卷
广西壮族自治区玉林市博白县五校2023-2024学年高二上学期12月联考数学试卷宁夏回族自治区银川市贺兰县第一中学2023-2024学年高二上学期期末复习数学试题(三)(已下线)专题27 直线与椭圆的位置关系及椭圆的弦长问题、面积问题(期末大题1)2023-2024学年高二数学上学期期末题型秒杀技巧及专项练习(人教A版2019)(已下线)3.1.2 椭圆的简单几何性质【第一练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)2.5.2 椭圆的几何性质——随堂检测
解题方法
3 . 已知数列 的前
的前 项和为
项和为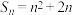 .
.
(1)求 的通项公式;
的通项公式;
(2)若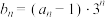 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为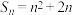 .
.(1)求
 的通项公式;
的通项公式;(2)若
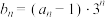 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
解题方法
4 . 已知过点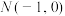 的直线l与抛物线
的直线l与抛物线 相交于
相交于 两点.
两点.
(1)求证: ;
;
(2)当 的面积等于
的面积等于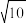 时,求直线l的方程.
时,求直线l的方程.
 的直线l与抛物线
的直线l与抛物线 相交于
相交于 两点.
两点.(1)求证:
 ;
;(2)当
 的面积等于
的面积等于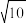 时,求直线l的方程.
时,求直线l的方程.
您最近一年使用:0次
名校
解题方法
5 . 已知直线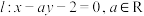 .
.
(1)求证:直线 与圆
与圆 恒有公共点;
恒有公共点;
(2)若直线 与圆心为
与圆心为 的圆
的圆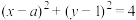 相交于
相交于 两点,且
两点,且 为直角三角形,求
为直角三角形,求 的值.
的值.
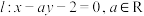 .
.(1)求证:直线
 与圆
与圆 恒有公共点;
恒有公共点;(2)若直线
 与圆心为
与圆心为 的圆
的圆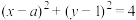 相交于
相交于 两点,且
两点,且 为直角三角形,求
为直角三角形,求 的值.
的值.
您最近一年使用:0次
名校
6 . 如图,在四面体 中,
中, ,
, 分别是线段
分别是线段 ,
, 上的点且
上的点且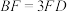 ,
,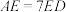 ,
, ,
,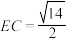 ,
,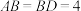 ,
, ,
,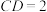 .
.
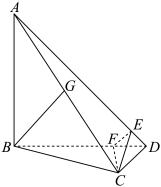
(1)证明: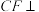 平面
平面 ;
;
(2)在线段 上是否存在点
上是否存在点 ,使得
,使得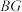 与平面
与平面 所成角的正弦值为
所成角的正弦值为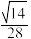 ?若存在,求
?若存在,求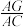 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,
中, ,
, 分别是线段
分别是线段 ,
, 上的点且
上的点且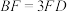 ,
,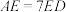 ,
, ,
,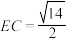 ,
,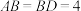 ,
, ,
,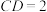 .
.
(1)证明:
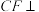 平面
平面 ;
;(2)在线段
 上是否存在点
上是否存在点 ,使得
,使得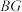 与平面
与平面 所成角的正弦值为
所成角的正弦值为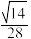 ?若存在,求
?若存在,求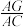 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
解题方法
7 . 设 分别是椭圆
分别是椭圆 的左、右焦点,当
的左、右焦点,当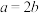 时,点P在椭圆上,且
时,点P在椭圆上,且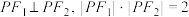 .
.
(1)求椭圆C的方程;
(2)直线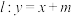 与椭圆C交于A,B两点,若
与椭圆C交于A,B两点,若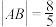 ,求实数m的值.
,求实数m的值.
 分别是椭圆
分别是椭圆 的左、右焦点,当
的左、右焦点,当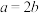 时,点P在椭圆上,且
时,点P在椭圆上,且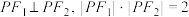 .
.(1)求椭圆C的方程;
(2)直线
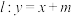 与椭圆C交于A,B两点,若
与椭圆C交于A,B两点,若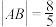 ,求实数m的值.
,求实数m的值.
您最近一年使用:0次
解题方法
8 . 已知点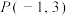 ,直线
,直线 .
.
(1)求经过点 且与直线
且与直线 平行的直线方程;
平行的直线方程;
(2)求经过点 且与直线
且与直线 垂直的直线方程.
垂直的直线方程.
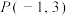 ,直线
,直线 .
.(1)求经过点
 且与直线
且与直线 平行的直线方程;
平行的直线方程;(2)求经过点
 且与直线
且与直线 垂直的直线方程.
垂直的直线方程.
您最近一年使用:0次
2023-12-26更新
|
364次组卷
|
4卷引用:广西壮族自治区崇左市大新县民族高级中学2023-2024学年高二上学期期中考试数学试题
9 . 安徽新高考改革方案正式公布,根据改革方案,计入高考总分的考试科目共有6门,即“3+1+2”,“3”为语文、数学、外语3门全国统一考试科目,不分文理科,使用全国卷,选择性考试科目为思想政治、历史、地理、物理、化学、生物学6门.由考生根据报考高校要求,结合自身特长兴趣,首先在物理和历史中选择1门,再从思想政治、地理、化学、生物学中选择2门.
附表:
 ,
,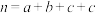 .
.
(1)若某学生根据方案从选择性考试科目中随机选择三科,求该生恰好选到政史地的概率;
(2)由于物理和历史两科必须选择1科,某校想了解学生选科的需求,随机选取100名学生进行调查,得到如下统计数据,判断是否有99%的把握认为“选科与性别有关”?
附表:
 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 ,
,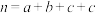 .
.(1)若某学生根据方案从选择性考试科目中随机选择三科,求该生恰好选到政史地的概率;
(2)由于物理和历史两科必须选择1科,某校想了解学生选科的需求,随机选取100名学生进行调查,得到如下统计数据,判断是否有99%的把握认为“选科与性别有关”?
| 选择物理 | 选择历史 | 合计 | |
| 男 | 40 | 10 | 50 |
| 女 | 30 | 20 | 50 |
| 合计 | 70 | 30 | 100 |
您最近一年使用:0次
名校
解题方法
10 . 记 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,已知
,已知 ,
, ,
, ,
,
(1)求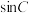 ;
;
(2)求 的面积.
的面积.
 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,已知
,已知 ,
, ,
, ,
,(1)求
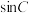 ;
;(2)求
 的面积.
的面积.
您最近一年使用:0次



