名校
解题方法
1 . 在 中,
中,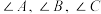 对应的边分别为
对应的边分别为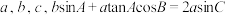 .
.
(1)求 ;
;
(2)奥古斯丁•路易斯・柯西,法国著名数学家.柯西在数学领域有非常高的造诣.很多数学的定理和公式都以他的名字来命名,如柯西不等式、柯西积分公式.其中柯西不等式在解决不等式证明的有关问题中有着广泛的应用.
①用向量证明二维柯西不等式: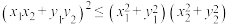 ;
;
②已知三维分式型柯西不等式: ,当且仅当
,当且仅当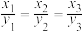 时等号成立.若
时等号成立.若 是
是 内一点,过
内一点,过 作
作 的垂线,垂足分别为
的垂线,垂足分别为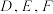 ,求
,求 的最小值.
的最小值.
 中,
中,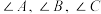 对应的边分别为
对应的边分别为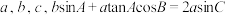 .
.(1)求
 ;
;(2)奥古斯丁•路易斯・柯西,法国著名数学家.柯西在数学领域有非常高的造诣.很多数学的定理和公式都以他的名字来命名,如柯西不等式、柯西积分公式.其中柯西不等式在解决不等式证明的有关问题中有着广泛的应用.
①用向量证明二维柯西不等式:
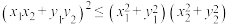 ;
;②已知三维分式型柯西不等式:
 ,当且仅当
,当且仅当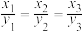 时等号成立.若
时等号成立.若 是
是 内一点,过
内一点,过 作
作 的垂线,垂足分别为
的垂线,垂足分别为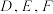 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024-05-12更新
|
467次组卷
|
5卷引用:【江苏专用】高一下学期期末模拟测试A卷
(已下线)【江苏专用】高一下学期期末模拟测试A卷山东省实验中学2023-2024学年高一下学期4月期中考试数学试题(已下线)专题05 解三角形(2)-期末考点大串讲(人教B版2019必修第四册)山东省青岛市即墨区第一中学2023-2024学年高一下学期第二次月考数学试题广东省广州市真光中学2023-2023学年高一下学期月考数学试题
解题方法
2 . 拉格朗日中值定理是微分学的基本定理之一,其内容为:如果函数 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且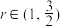 .
.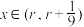 时,
时,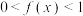 ;
;
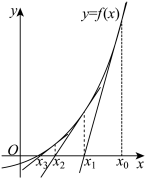
(2)从图形上看,函数 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得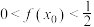 ,然后在点
,然后在点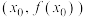 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列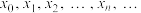 .
.
①当 时,证明:
时,证明: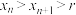 ;
;
②根据①的结论,运用数学归纳法可以证得: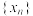 为递减数列,且
为递减数列,且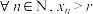 .请以此为前提条件,证明:
.请以此为前提条件,证明: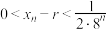 .
.
 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且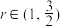 .
.
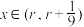 时,
时,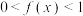 ;
;(2)从图形上看,函数
 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得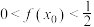 ,然后在点
,然后在点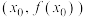 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列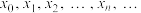 .
.①当
 时,证明:
时,证明: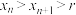 ;
;②根据①的结论,运用数学归纳法可以证得:
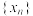 为递减数列,且
为递减数列,且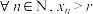 .请以此为前提条件,证明:
.请以此为前提条件,证明: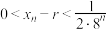 .
.
您最近一年使用:0次
名校
解题方法
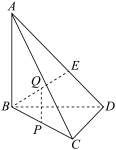
3 . 我国古代数学名著《九章算术》中,称四面都为直角三角形的三棱锥为“鳖臑”.如图,在三棱锥 中,
中, 平面
平面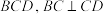 .
. 为鳖臑;
为鳖臑;
(2)若 为
为 上一点,点
上一点,点 分别为
分别为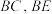 的中点.平面
的中点.平面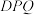 与平面
与平面 的交线为
的交线为 .
.
①证明:直线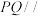 平面
平面 ;
;
②判断 与
与 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
 中,
中, 平面
平面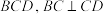 .
.
 为鳖臑;
为鳖臑;(2)若
 为
为 上一点,点
上一点,点 分别为
分别为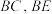 的中点.平面
的中点.平面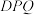 与平面
与平面 的交线为
的交线为 .
.①证明:直线
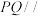 平面
平面 ;
;②判断
 与
与 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
您最近一年使用:0次
2024-04-29更新
|
1548次组卷
|
6卷引用:江苏省无锡市第一中学2023-2024学年高一下学期4月期中考试数学试题
名校
4 . “弦图”是我国古代三国时期的数学家赵爽为《周髀算经》作注时为证明勾股定理所绘制,此图曾作为2002年在北京召开的第24届国际数学家大会的会标如图,在正方形 中,有4个全等的直角三角形,若图中
中,有4个全等的直角三角形,若图中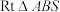 的两锐角分别为
的两锐角分别为 ,且小正方形与大正方形的面积之比为
,且小正方形与大正方形的面积之比为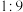 ,则
,则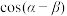 的值为
的值为________ .
 中,有4个全等的直角三角形,若图中
中,有4个全等的直角三角形,若图中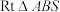 的两锐角分别为
的两锐角分别为 ,且小正方形与大正方形的面积之比为
,且小正方形与大正方形的面积之比为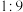 ,则
,则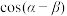 的值为
的值为
您最近一年使用:0次
名校
5 . 数学里有一种证明方法叫做Proofwithoutwords,也被称为无字证明,是指仅用图象而无需文字解释就能不证自明的数学命题,由于这种证明方法的特殊性,无字证明被认为比严格的数学证明更为优雅与有条理.如下图,点 为半圆
为半圆 上一点,
上一点, ,垂足为
,垂足为 ,记
,记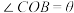 ,则由
,则由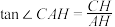 可以直接证明的三角函数公式是( )
可以直接证明的三角函数公式是( )
 为半圆
为半圆 上一点,
上一点, ,垂足为
,垂足为 ,记
,记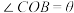 ,则由
,则由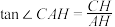 可以直接证明的三角函数公式是( )
可以直接证明的三角函数公式是( )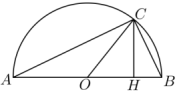
A. | B. | C. | D.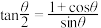 |
您最近一年使用:0次
名校
解题方法
6 . 固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程为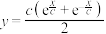 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数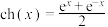 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.
(1)类比正、余弦函数导数之间的关系,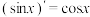 ,
,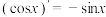 ,请写出
,请写出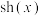 ,
,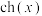 具有的类似的性质(不需要证明);
具有的类似的性质(不需要证明);
(2)当 时,
时,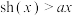 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)求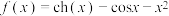 的最小值.
的最小值.
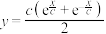 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数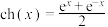 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.(1)类比正、余弦函数导数之间的关系,
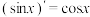 ,
,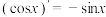 ,请写出
,请写出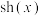 ,
,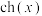 具有的类似的性质(不需要证明);
具有的类似的性质(不需要证明);(2)当
 时,
时,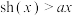 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)求
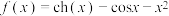 的最小值.
的最小值.
您最近一年使用:0次
2024-03-10更新
|
1098次组卷
|
16卷引用:模块一 专题3 《导数在研究函数极值和最值中的应用》B提升卷(苏教版)
(已下线)模块一 专题3 《导数在研究函数极值和最值中的应用》B提升卷(苏教版)(已下线)模块三 专题3 高考新题型专练 专题2 新定义专练(苏教版)广西示范性高中2023-2024学年高二下学期3月调研测试数学试卷(已下线)模块一 专题3 导数在研究函数极值和最值中的应用(B)(已下线)综合检测卷(数列+导数)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)湖北省荆州市沙市中学2023-2024学年高二下学期3月月考数学试题广东省揭阳市惠来县第一中学2023-2024学年高二下学期3月月考数学试题(已下线)模块四 专题1 高考新题型专练(新定义专练)(人教A)(高二)(已下线)高二下学期第一次月考模拟卷(新题型)(导数+计数原理)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019)河北省正定中学2023-2024学年高二下学期第一次月考数学试题河北省邯郸市大名县第一中学2023-2024学年高二下学期3月月考数学试卷山东省临沂市第二十四中学2023-2024学年高二下学期3月月考数学试题吉林省长春外国语学校2023-2024学年高二下学期4月月考数学试卷广东省深圳市高级中学(集团)2023-2024学年高二下学期期中考试数学试卷(已下线)上海市四校(复兴高级中学、松江二中、奉贤中学、金山中学)2024届高三下学期3月联考数学试题变式题17-21福建省龙岩市连城县第一中学2023-2024学年高二下学期5月月考(2)数学试题
7 . 希腊数学家帕普斯在他的著作《数学汇篇》中,完善了欧几里得关于圆锥曲线的统一定义,并对这一定义进行了证明,他指出,到定点的距离与到定直线的距离的比是常数 的点的轨迹叫做圆锥曲线:当
的点的轨迹叫做圆锥曲线:当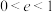 时,轨迹为椭圆;当
时,轨迹为椭圆;当 时,轨迹为抛物线;当
时,轨迹为抛物线;当 时,轨迹为双曲线,则方程
时,轨迹为双曲线,则方程 表示的圆锥曲线为( )
表示的圆锥曲线为( )
 的点的轨迹叫做圆锥曲线:当
的点的轨迹叫做圆锥曲线:当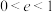 时,轨迹为椭圆;当
时,轨迹为椭圆;当 时,轨迹为抛物线;当
时,轨迹为抛物线;当 时,轨迹为双曲线,则方程
时,轨迹为双曲线,则方程 表示的圆锥曲线为( )
表示的圆锥曲线为( )| A.椭圆 | B.双曲线 | C.抛物线 | D.以上都不对 |
您最近一年使用:0次
2024-01-27更新
|
356次组卷
|
2卷引用:江苏省盐城市响水中学2023-2024学年高二上学期期末数学试题
名校
解题方法
8 . 若 内一点
内一点 满足
满足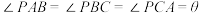 ,则称点
,则称点 为
为 的布洛卡点,
的布洛卡点, 为
为 的布洛卡角.如图,已知
的布洛卡角.如图,已知 中,
中, ,
, ,
,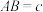 ,点
,点 为的布洛卡点,
为的布洛卡点, 为
为 的布洛卡角.
的布洛卡角. ,且满足
,且满足 ,求
,求 的大小.
的大小.
(2)若 为锐角三角形.
为锐角三角形.
(ⅰ)证明: .
.
(ⅱ)若 平分
平分 ,证明:
,证明: .
.
 内一点
内一点 满足
满足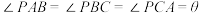 ,则称点
,则称点 为
为 的布洛卡点,
的布洛卡点, 为
为 的布洛卡角.如图,已知
的布洛卡角.如图,已知 中,
中, ,
, ,
,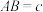 ,点
,点 为的布洛卡点,
为的布洛卡点, 为
为 的布洛卡角.
的布洛卡角.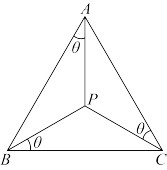
 ,且满足
,且满足 ,求
,求 的大小.
的大小.(2)若
 为锐角三角形.
为锐角三角形.(ⅰ)证明:
 .
.(ⅱ)若
 平分
平分 ,证明:
,证明: .
.
您最近一年使用:0次
2024-04-30更新
|
1949次组卷
|
6卷引用:专题06 解三角形综合大题归类(2) -期末考点大串讲(苏教版(2019))
(已下线)专题06 解三角形综合大题归类(2) -期末考点大串讲(苏教版(2019))河北省部分高中2024届高三下学期二模考试数学试题(已下线)2024年普通高等学校招生全国统一考试数学押题卷(一)(已下线)压轴题07三角函数与正余弦定理压轴题9题型汇总-1湖南省长沙市长郡中学2024届高考适应考试(三)数学试题(已下线)专题02 第六章 解三角形及其应用-期末考点大串讲(人教A版2019必修第二册)
名校
解题方法
9 . 三等分角是古希腊几何尺规作图的三大问题之一,如今数学上已经证明三等分任意角是尺规作图不可能问题,如果不局限于尺规,三等分任意角是可能的.下面是数学家帕普斯给出的一种三等分角的方法:已知角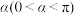 的顶点为
的顶点为 ,在
,在 的两边上截取
的两边上截取 ,连接
,连接 ,在线段
,在线段 上取一点
上取一点 ,使得
,使得 ,记
,记 的中点为
的中点为 ,以
,以 为中心,
为中心, 为顶点作离心率为2的双曲线
为顶点作离心率为2的双曲线 ,以
,以 为圆心,
为圆心, 为半径作圆,与双曲线
为半径作圆,与双曲线 左支交于点
左支交于点 (射线
(射线 在
在 内部),则
内部),则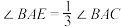 .在上述作法中,以
.在上述作法中,以 为原点,直线
为原点,直线 为
为 轴建立如图所示的平面直角坐标系,若
轴建立如图所示的平面直角坐标系,若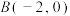 ,点
,点 在
在 轴的上方.
轴的上方. 的方程;
的方程;
(2)若过点 且与
且与 轴垂直的直线交
轴垂直的直线交 轴于点
轴于点 ,点
,点 到直线
到直线 的距离为
的距离为 .
.
证明:①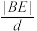 为定值;
为定值;
②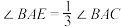 .
.
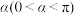 的顶点为
的顶点为 ,在
,在 的两边上截取
的两边上截取 ,连接
,连接 ,在线段
,在线段 上取一点
上取一点 ,使得
,使得 ,记
,记 的中点为
的中点为 ,以
,以 为中心,
为中心, 为顶点作离心率为2的双曲线
为顶点作离心率为2的双曲线 ,以
,以 为圆心,
为圆心, 为半径作圆,与双曲线
为半径作圆,与双曲线 左支交于点
左支交于点 (射线
(射线 在
在 内部),则
内部),则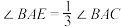 .在上述作法中,以
.在上述作法中,以 为原点,直线
为原点,直线 为
为 轴建立如图所示的平面直角坐标系,若
轴建立如图所示的平面直角坐标系,若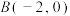 ,点
,点 在
在 轴的上方.
轴的上方.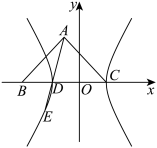
 的方程;
的方程;(2)若过点
 且与
且与 轴垂直的直线交
轴垂直的直线交 轴于点
轴于点 ,点
,点 到直线
到直线 的距离为
的距离为 .
.证明:①
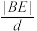 为定值;
为定值;②
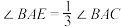 .
.
您最近一年使用:0次
10 . 勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”. 中国是发现和研究勾股定理最古老的国家之一. 据记载,在公元前1120年,商高答周公曰“故折矩,以为勾广三,股修四,径隅五,既方之,外半其一矩,环而共盘,得成三四五,两矩共长二十有五,是谓积矩. ”因此,勾股定理在中国又称“商高定理”. 数百年后,希腊数学家毕达哥拉斯发现并证明了这个定理,因此“勾股定理”在西方被称为“毕达哥拉斯定理”. 三国时期,吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明. 如图所示的勾股圆方图中,四个全等的直角三角形与中间的小正方形拼成一个大正方形. 若中间小正方形面积(阴影部分)是大正方形面积一半,则直角三角形中较小的锐角 的大小为
的大小为_________ .
 的大小为
的大小为
您最近一年使用:0次



